Estimate the solution to the system of equations.

(1, 1.5)
A video game streamer gains followers quickly after a tournament. She began with 200 followers. Each day, her number of followers increases by
3/2
times the previous day's total.
Identify the initial value, growth/decay factor, and whether the function is growing or decaying.
Initial Value: 200
Growth / Factor:
3/2
The function is growing exponentially.
"Factor " x^2+7x+12.
(x+3)(x+4)
Solve the quadratic equation by factoring:
x^2-7x+10=0
x = 5 or x = 2
Determine the axis of symmetry and vertex for the quadratic function,
f(x)=4x^2+32x+48
axis of symmetry: x = -2
vertex: (-2, -16)
Write the system of linear equations in slope-intercept form.

"red line: "y=1/2x+1
"blue line: "y=x+1/2
A scientist places a sample of a radioactive substance in a lab. The substance decays over time so that only 0.7 of it remains each hour. The initial mass of the sample is 200 grams. Write an exponential function that represents the situation.
f(x)=200*(0.7)^x
"Factor " 2x^2+5x+3
(2x+3)(x+1)
Find the solution(s) to the quadratic equation:
(x-4)^2=100
x = 14 or x = -6
Identify each of the following:
- y-intercept
- x-intercept(s) (if any)
- zero(s) (if any)
- Maximum or minimum vertex.
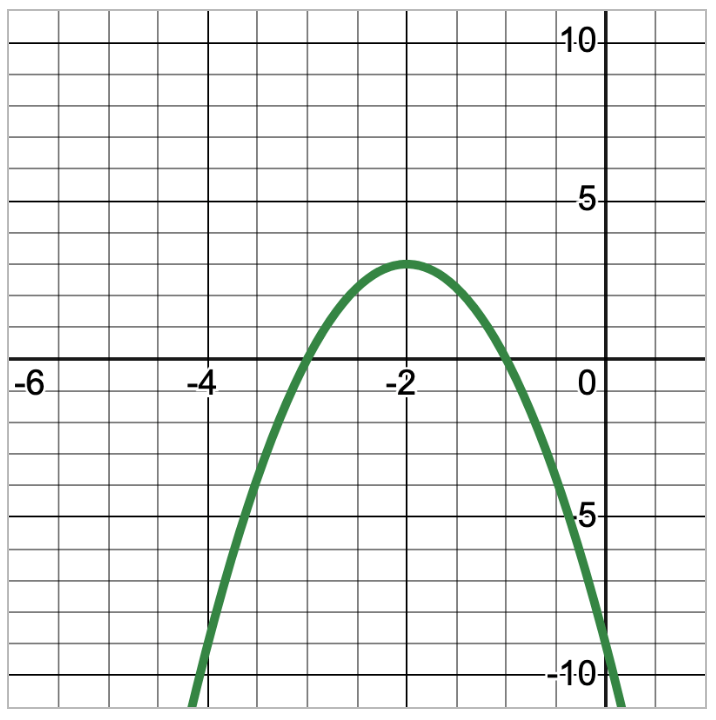
y-intercept: (0, -9)
x-intercepts: (-3, 0) and (-1, 0)
zeros: -3, -1
Maximum
Maria is buying cupcakes for her class party. She buys a total of 24 cupcakes, some are strawberry and some are chocolate. The strawberry cupcakes cost $2 each, while the chocolate cupcakes cost $1 each. Maria spent a total of $38 on the cupcakes. How many of each type of cupcake did Maria buy?
Hint: Set up and solve a system of linear equations.
s+c=24
2s+1c=38
Strawberry: 14
Chocolate: 10
"A bakery bakes a fresh batch of 50 cupcakes in the morning. As the day goes on, customers buy the cupcakes, and the number of cupcakes left decreases exponentially. After each hour, only 80% of the cupcakes from the previous hour remain. How many cupcakes will be left after 5 hours?
Hint: Write an exponential function.
f(x)=50*(0.8)^x
16 or 17
"Factor " 3x^2-14x-5.
(3x+1)(x-5)
Find the solution(s) to the quadratic equation, using any method you’d like (i.e., factoring, completing the square, or quadratic formula):
5x^2+25x-59=11
x = -7 or x = 2
How do different values of a affect
f(x)=ax^2?
- larger values of a make the parabola narrower
- smaller values of a make the parabola wider
- negative a flips the parabola downward