Basic Absolute Value
Slides
Stretches
Reflections
Multiple Transformations
100
Evaluate the following absolute expression
2|-6+1|-|3(2-5)|
1
100
How do you identify slides from an equation? Explain the difference between Horizontal and Vertical slides
H slides: + or - on the inside
V slides: + or - on the outside
100
Write an example of a vertical stretch and a horizontal stretch of factor 5 on the absolute value parent function. (Hint: 2 functions needed)
V Stretch:
f(x)=5abs(x)
H Stretch:
f(x)=1/5abs(x)
100
Which axis does a horizontal reflection reflect across?
Which axis does a vertical reflection reflect across?
H: y-axis
V: x-axis
100
Identify all transformations in the following absolute value function
f(x)=-2|x+4|
Vertical Reflection
Vertical stretch factor 2
Horizontal shift 4 to the left
200
List the solutions to the following absolute value equation
abs(x)=10
x = 10, -10
200
Identify all slides in the following absolute value function
f(x) = -4|x + 1|- 18
Slide 1 Left
18 Down
200
Identify all stretches in the following absolute value function
f(x)=-abs(x/4-17)+12
horizontal stretch factor 4
200
Identify all reflections in the following absolute value function
f(x)=2|x-3|+4
NONE
(No reflections)
(or you could say a double vertical reflection)
200
Identify all transformations in the following absolute value function
f(x)=-3abs(x-42)+63
vertical reflection
vertical stretch factor 3
shift 42 right, 63 up
300
Compute the following absolute value expression
|4-10|/-2*|(-4-6)/5|
-6
300
Write the absolute value parent function with the following transformations applied:
Shift 12 up, 216 to the right
f(x)=abs(x-216)+12
300
Write the absolute value parent function with the following transformations applied:
Vertical stretch factor 3
Horizontal stretch factor 5
f(x)=3|x/5|
300
Write the absolute value parent function with the following transformations applied:
2 horizontal reflections
5 vertical reflections
f(x)=-abs(x)
300
Write a quadratic function (x2) with the following transformations applied:
vertical stretch factor 5
vertical reflection
slide left 9, down 3
f(x)=-5(x+9)^2-3
400
State the domain and range of the absolute value parent function
D: All real numbers,
(-infty, infty)
R:
[0, infty)
400
Identify all slides, and write the equation of the absolute value function below
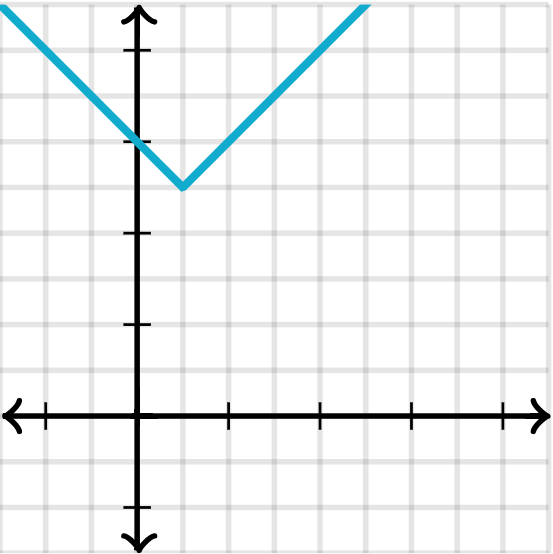
f(x)=abs(x-1)+5
400
Identify all stretches, and write the equation of the absolute value function below
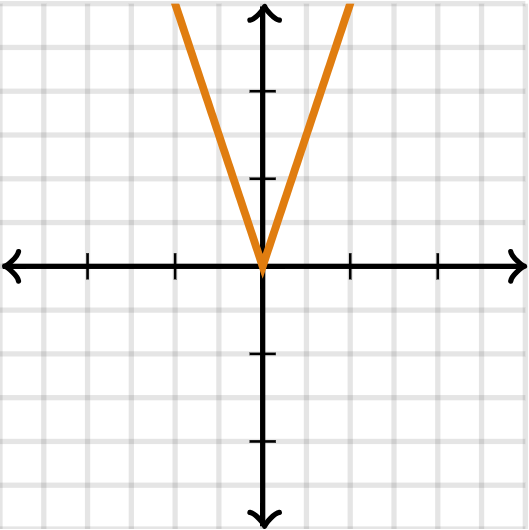
f(x)=3|x|
400
Identify all slides and reflections and write the absolute value function graphed below
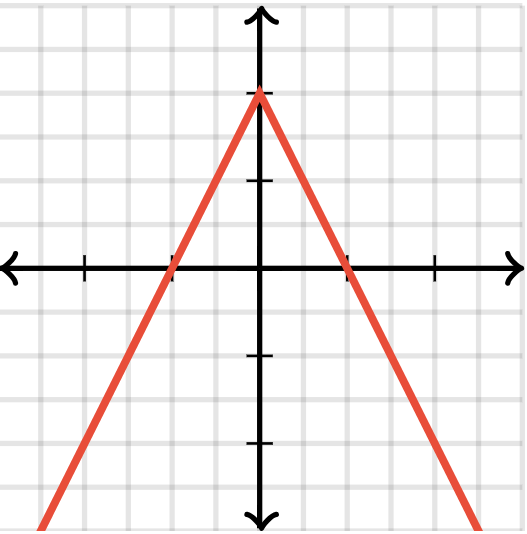
f(x)=-|x|+2
400
Below is a photo of a transformed quadratic function. Identify all transformations and write the function below:
(hint: a normal quadratic function goes over 1, up 1)
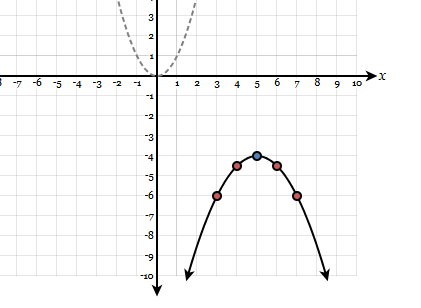
f(x)=-1/2(x-5)^2-4
500
write an absolute value equation/function that has NO SOLUTION
Many different answers
Example answer:
|2x+5|=-3
500
Write the function with the following slides applied:
Parent function: sqrt(x)
Shifts: 16 to the left, 190 down
f(x)=sqrt(x+16)-190
500
Write the function with the following transformations applied
Parent function: x^3
Transformations: Vertical stretch factor 15
f(x)=15x^3
500
Write the function with the following transformations applied
Parent Function: Quadratic
Transformations applied: Vertical reflection,
horizontal stretch factor 4
f(x)= -1/4x^2
500
Write the function with the following transformations applied
Parent function: f(x)=cos(x)
Transformations:
shift up 5 right 4
vertical stretch factor 4
vertical reflection
f(x)=-4cos(x-4)+5