Which Method is Best?
Solve by Graphing
Solve by Substitution
Solve by Elimination
Solution? Yes or No
100
Which method would be best to solve the system below? (Graphing, Substitution, or Elimination)
x = 2
2x + 3y = 13
Substitution
x is already solved!
Plug in 2 directly in for x and solve for y!
100
When two equations are graphed, where is the solution?
Where the lines cross each other.
100
Solve the system by Substitution method:
y = -2
4x - 3y = 18
(3, -2)
4x - 3(-2) = 18
4x = 12
x = 3
100
Solve the system using Elimination method:
x - y = 11
2x + y = 19
(10, -1)
Get rid of the y by adding!
3x = 30
x = 10
100
Is (-1, 1) a solution to the system:
y = x - 2
2x + y = 1
No
y = x - 2
1 = (-1) - 2
1 = -3 Not true!
200
Which method would be best to solve the system below? (Graphing, Substitution, or Elimination)
y = -3x + 2
6x + 2y = 1
Substitution
y is already solved for, just plug it in!
200
If the system of equations is graphed with two PARALLEL lines, how many solutions are there?
No Solution, One Solution, or Infinitely Many Solutions
No Solution
The lines don't cross!
200
Solve the system by Substitution method:
2x - 3y = -1
y = x - 1
(4, 3)
2x - 3(x - 1) = -1
-x + 3 = -1
-x = -4 ---> x = 4
200
Solve the system by using the Elimination method:
-6x + 5y = 1
6x + 4y = -10
(-1, -1)
Get rid of x by adding!
9y = -9
y = -1
200
Is (-4, 7) a solution to the system:
y = -2x - 1
x + y = 3
Yes!
7 = -2(-4) - 1
-4 + 7 = 3
Both are true!
300
Which method would be best to solve the system below? (Graphing, Substitution, or Elimination)
3x + 2y = 4
-3x + y = 2
Elimination
Get rid of the x by adding!
300
What is the solution to the system graphed below?
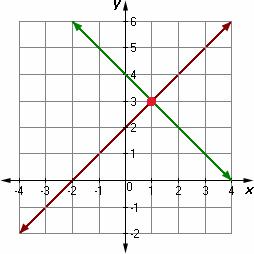
(1, 3)
x = 1, y = 3
300
Solve the system by Substitution method:
y = x
y = -x + 6
(3, 3)
x = -x + 6
2x = 6
x = 3
300
Solve the system by using the Elimination method:
4x + 2y = 8
3x + 2y = 6
(2, 0)
Get rid of the y by subtracting!
x + 0 = 2
x = 2
300
Is (4, 7) a solution to the system:
y = -2x - 1
x = -y + 3
No!
7 = -2(4) - 1 = -8 - 1
4 = -7 + 3
Neither one works
400
Which method would be best to solve the system below? (Graphing, Substitution, or Elimination)
y = 1/2x + 2
y = 2x - 7
Graphing
Both equations are in y = mx + b form!
(Substitution could also work here)
400
What is the solution to the system graphed below?
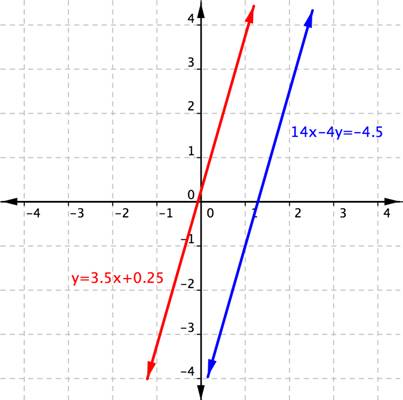
No Solution
Parallel lines don't have a point of intersection!
400
Solve the system by Substitution method:
y = 5x - 1
2y = 3x + 12
(2, 9)
2(5x - 1) = 3x + 12
10x - 2 = 3x + 12
7x = 14
400
Solve the system by using the Elimination method:
-3x + 3y = 3
-3x + 6y = -12
(-6, -5)
Get rid of the x by subtracting!
-3y = 15
y = -5
400
Is (2, -1) a solution to the system:
y = 1/2x
y = -x + 3
Nope.
-1 = 1/2(2)
-1 = -2 + 3
Neither of these are true.
500
Which method would be best to solve the system below? (Graphing, Substitution, or Elimination)
4x + y = 16
2x + 3y = -2
Elimination
Multiply the bottom equation by -2
(Or Substitution; Solve the first equation for y)
500
Does the system below have one solution, no solution, or infinitely many solutions?
y = 2/3x + 11
y = 2/3x - 4
No Solution
The slopes are the SAME, so the lines are PARALLEL
No point of intersection
500
Solve the system by Substitution method:
-5x + y = -3
3x - 8y = 24
(0, -3)
y = -3 + 5x
3x - 8(-3 + 5x) = 24
3x + 24 - 40x = 24 ---> -37x = 0
500
Solve the system by using the Elimination method:
5x + y = 9
10x - 7y = -18
(1, 4)
Multiply the top equation by -2
-10x - 2y = -18
10x - 7y = -18 ----> Then add!
500
Is (3, -1) a solution to the system:
x - 2y = 5
2x - y = 7
Yes!
3 - 2(-1) = 3 + 2 = 5
2(3) - (-1) = 6 + 1 = 7
Both are true!