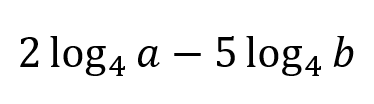Log Functions
Properties of Logs
Common/Natural Logs
Concepts
Potpourri
100
The exponential form of this is what?
100
This is the definition of one of the properties of logarithms
What is the Product Property of Logarithms
100
This number is the base of the Natural Logarithm
What is e or Euler's number
100
This can be simplified:
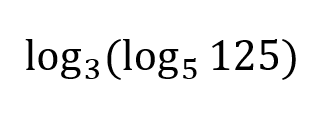
What is 1
100
This is one of the properties of logarithms:
What is the Quotient Property of Logarithms
200
The one word description of a logarithm
A logarithm is an exponent
200
This can be written as a single logarithm:
What is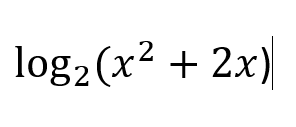 
200
A logarithm with no explicit base is named this type of a logarithm
What is a Common Logarithm
200
This can be simplified:
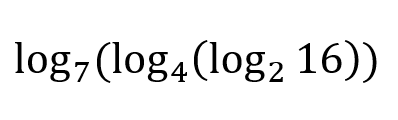
0
200
This is what we are doing to the base numbers when we add their logarithms
What is multiplication
300
A logarithmic function is the inverse of these functions.
What are Exponential Functions
300
This can be written as a single logarithm
What is:
300
This is how x varies with y in the equation below:
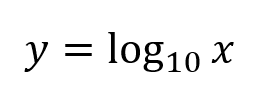
What is exponentially
300
Which is larger can be explained without a calculator:
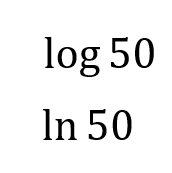
What is: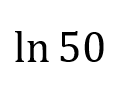 
300
This is what we are doing to the base numbers when we subtract their logarithms
What is division
400
This is the domain of the logarithm function
What is :
400
This can be written as the sum and difference of multiple logarithms:
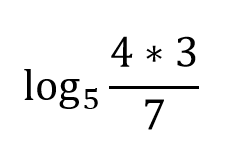
What is:
400
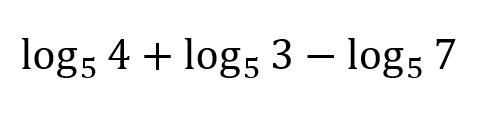
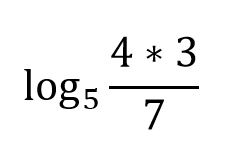
This has an exact value:
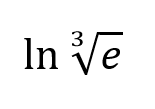
What is 1/3
400
This could be done to plot the points of an exponentials function corresponding logarithm.
What is reverse x and y values
400
This logarithm can be rewritten:
What is: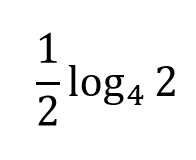 
500
Logarithms as well as exponential functions are this special type of function.
What is "one-to-one functions"
500
This is a property of logarithms and has a value:
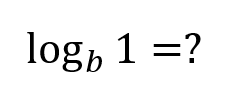
What is zero
500
This could be expressed as the quotient of two logs, both with base 10.
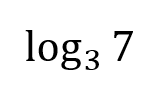
What is:
500
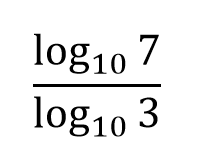
The graph of an exponential function and its corresponding logarithm is symmetric about this line
What is y = x
500
This can be written as the sum and difference of multiple logarithms:
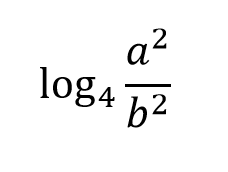
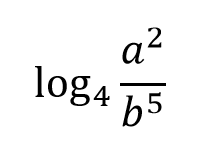
What is:
