Is this function represent exponential GROWTH or DECAY?
f(x) = 1.2(0.99)x
EXPONENTIAL DECAY
Consider the function:
f(x)=2(x-1) +5.
What is the parent function?
f(x) = 2x
Write the logarithm in EXPONENTIAL form.
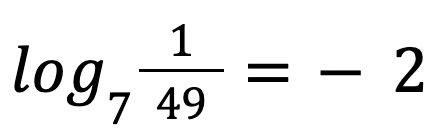
7^-2=1/49
What do you call of 2 value in the exponential equation?
f(x)=2∙5^x
INITIAL VALUE
When the base of this function is raised to an input of 0, the result is 1. So your are left with the coefficient being multiplied by 1. This means the coefficient is the INITIAL VALUE or what you started with before the function began to grow or decay.
Evaluate:
log7 721
21
Write the END BEHAVIOR of this graph.
x → -∞, y → x → +∞, y →
DAILY DOUBLE
x -> -oo, y -> 3
x -> +oo, y -> +oo
Consider the function: f(x) = 3(x+2) - 8.
What is the parent function? Describe all transformations the function has undergone from the parent function.
Parent function: f(x) = 3x
Transformations:
Horizontal translation: 2 units left
Vertical translation: 8 units down
Evaluate the logarithms below:
a) log2(64)
b) log5(125)
a) 6
b) 3
What do you call the 5 value in the logarithmic equation?
y = log5 x
Base
Solve for x:
log3 x = -4
x = 1/81
Solution:
3-4 = (1/3)4 = 1/81
Does this exponential function model GROWTH or DECAY?
y=0.75(7/6)^x+3
GROWTH
The common ratio (r) in this equation is greater than 1 which indicated decay (the outputs are getting bigger by a factor of 7/6 for every increase of 1 in the input.
Convert to exponential form: log3 81 = 4
34 = 81
Estimate the value of log3 (90) WITHOUT a calculator.
xapprox4.1
Since 34=81 and 35=243, we can see x must be between 4 and 5. Since 90 is much closer to 81 than 243, we can estimate the value to be slightly over 4.
Condense the expression:
DAILY DOUBLE
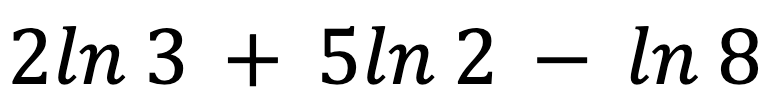
ln 36
Solve the equation.
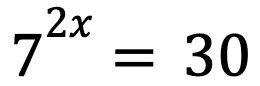
x is approximately 0.874
Write the exponential equation for the table below.
f(x) = 5(3)x
The blue graph is of f(x)=2x. Find the equation of the green graph g(x) which has been transformed.

g(x)=2^((x-4))-3
Graph:
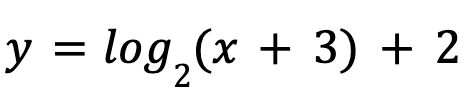
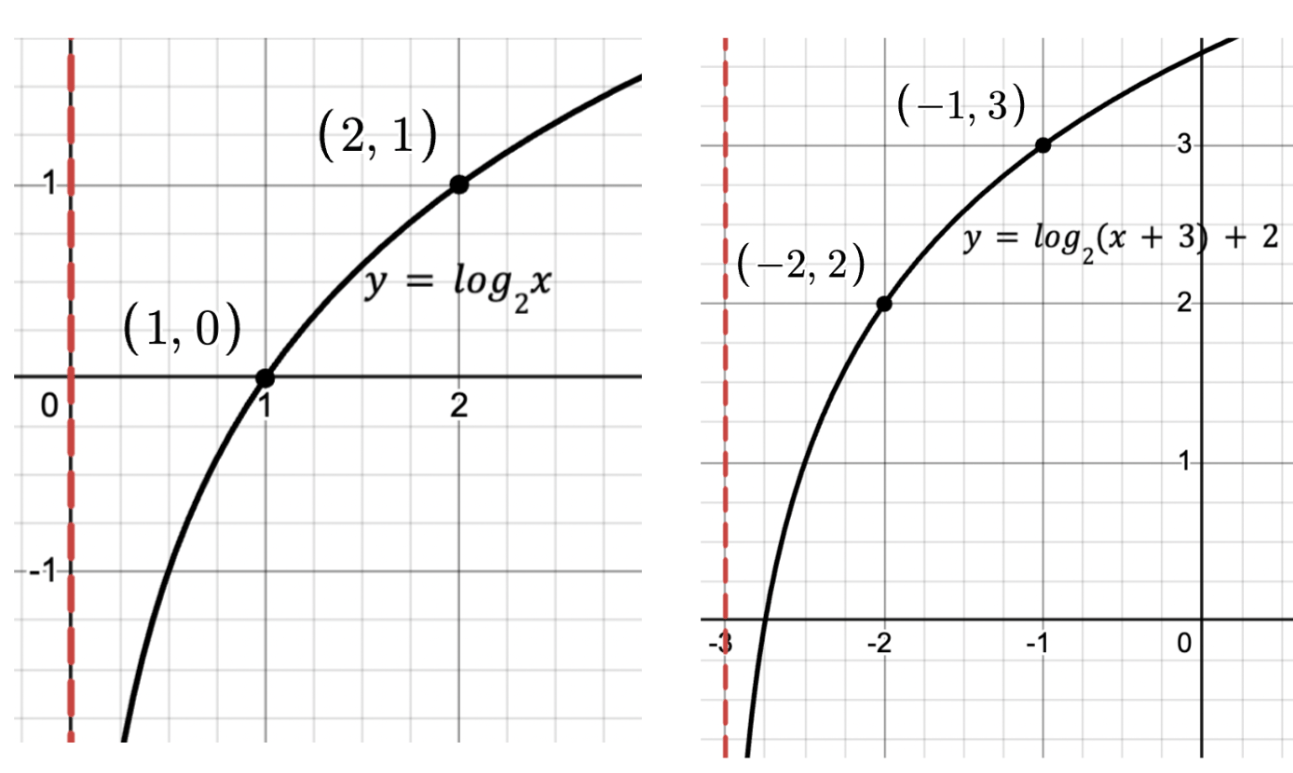
Use change of base formula to evaluate the logarithm:
about 1.750
Solve the equation:
x=104
Write the equation of the exponential graph.
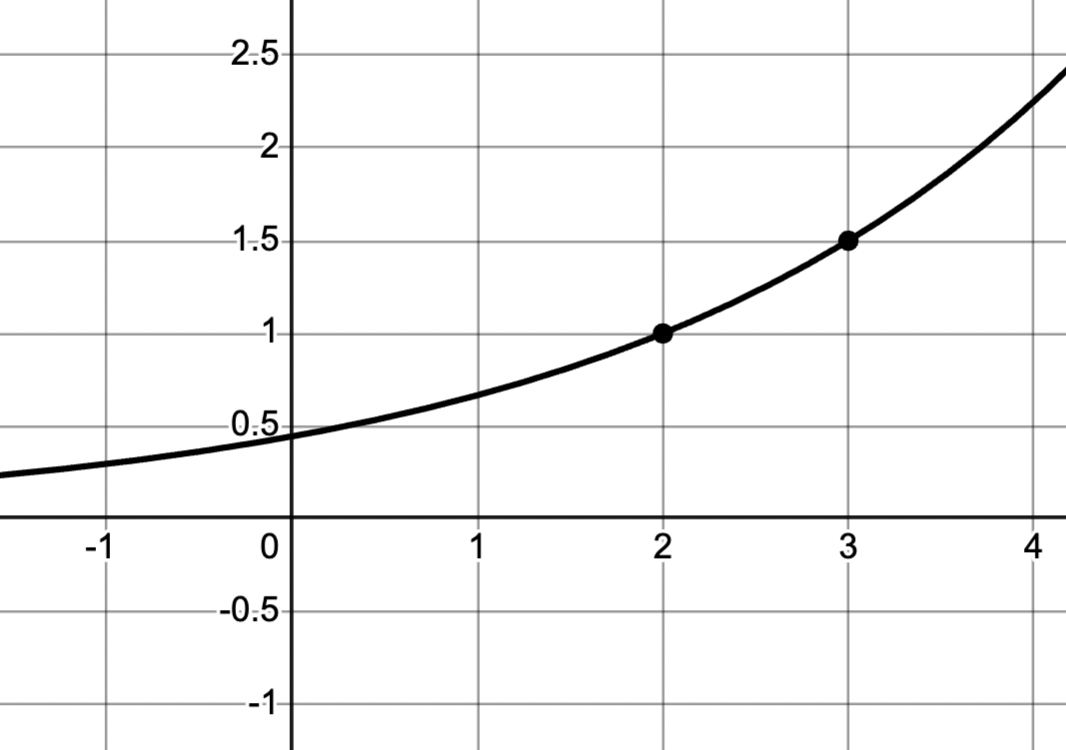
y=4/9(3/2)^x
y=0.\overline{4}(1.5)^x
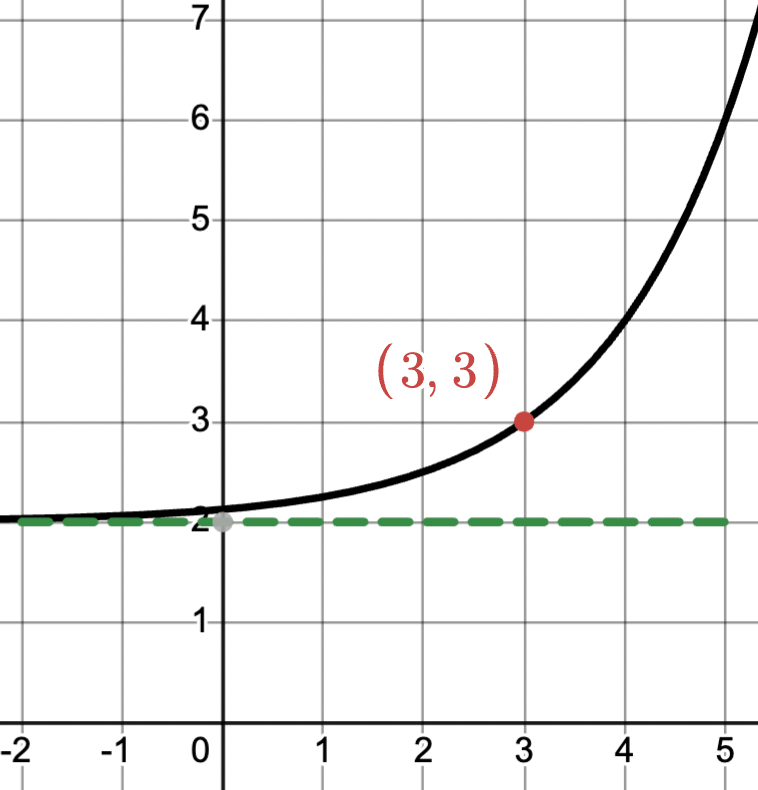
Graph the function:
f(x)=2(x-3) + 2.
Find the inverse of the exponential function.
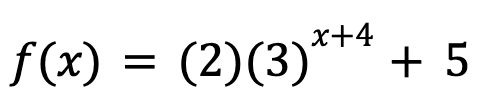
y=log_3((x-5)/2)-4
The inverse of an exponential function is a logarithm. So rewrite the original function in logarithmic form by switching x and y and then isolating y.
Convert this to logarithmic form: 45=1024
log4 1024 = 5
Solve the equation:
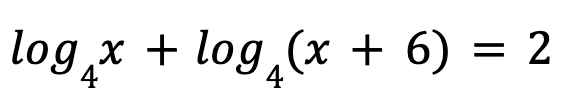
x=2