Create a new function, h(x), that transformations f(x) in the follow ways:
-reflection over the x-axis
-horizontal stretch by a factor of 2
-vertical translation up 3
h(x) = -f(1/2x) + 3
Solve for x.
6 + abs(9 + x) = 22
x = 7, -25
Solve for x. Write you answer in interval notation.
abs(x + 5)/2<= 2
[-9, -1]
Is the following function even, odd, or neither.
f(x) = -3x^5 - 7x + 5
neither
Solve.
2x + y = 5
3x - 3y = 3
(2, 1)
Create a new function, h(x), that transforms the function f(x) in the following ways:
-vertical stretch by a factor of 3
-reflection over the y-axis
-horizontal shrink by a factor of 3/4
h(x) = 3f(-4/3x)
Solve for x.
2abs(x - 4) + 3 = -19
no solution
Solve for x. Write your answer in interval notation.
-8abs(x - 10) < -112
(-oo, -4), (24, oo)
Describe the end behavior of the following function, using proper notation. Then describe domain and range in interval notation.
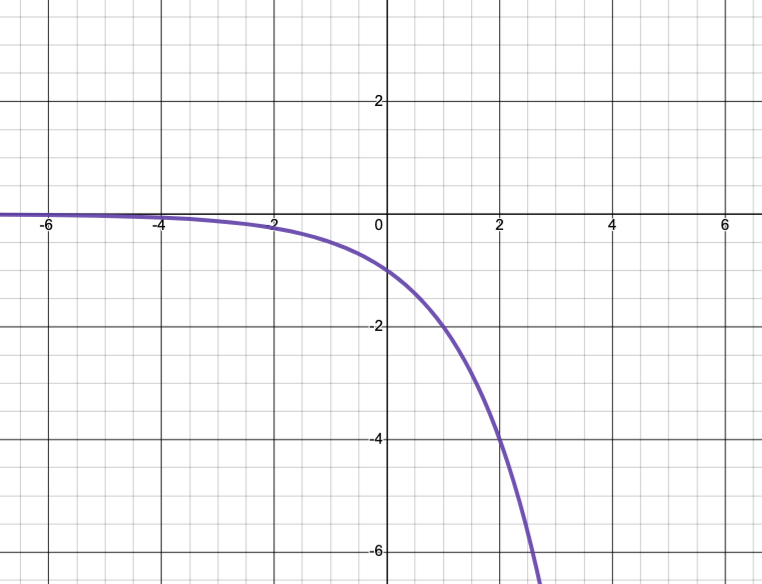
x -> oo, f(x) -> -oo
x->-oo, f(x) -> 0
D: (-oo, oo) R: (-oo, 0)
Solve.
4x - 2y = 0
-3x + 9y = 5
(1/3, 2/3)
Describe the transformations of the function below, f(x), in reference to the parent function, p(x)
p(x) = sqrtx, f(x) = -sqrt(3x + 6)
-reflection over the x-axis
-horizontal shrink by a factor of 1/3
-horizontal translation left 2
Graph the following function and determine the vertex:
y = 3abs(2x - 2) - 2
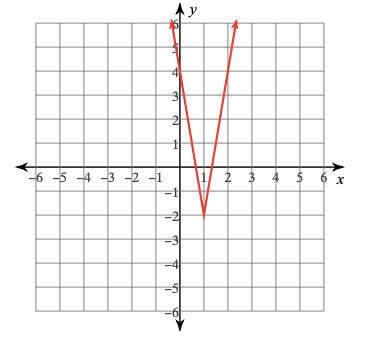
vertex: (1, -2)
Solve for x. Write your answer in interval notation:
9 + abs(-3 - p) <= -2
No Solution
Describe the end behavior of the following graph using proper notation. Then, describe the domain and range in interval notation.
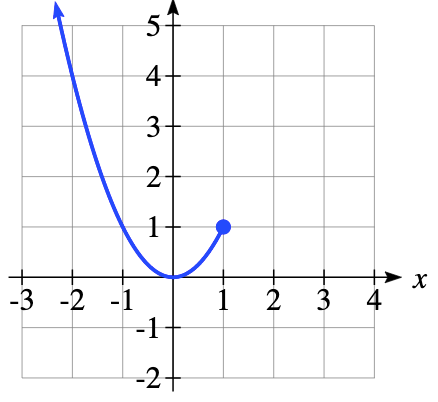
No end behavior on the right
x->-oo, f(x) -> oo
D: (-oo, 1] R: [0, oo)
Find the coordinates of the feasible region of the system below. Then, find the max and min values of the function for this region.
f(x, y) = 3x - 2y
y >= 2
1 <= x <= 5
y <= x + 3
vertices:
(1, 2), (1, 4), (5, 8), (5, 2)
Max: 11
Min: -5
Describe the transformations of the functions:
f(x) = 5/4f(-2x + 3) - 5
-vertical stretch by a factor of 5/4
-reflection over the y-axis
-horizontal shrink by a factor of 1/2
-horizontal translation right 3/2
-vertical translation down 5
Solve for x.
4abs(7x + 1) + 5 = 9
x = 0, -2/7
Solve for x. Write your answer in interval notation.
abs(8 - 3x) - 2 >= -6
(-oo, oo)
Describe where the function is increasing and decreasing, then where the function is positive and negative. Use interval notation:
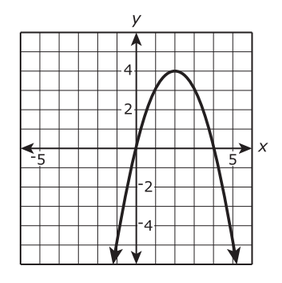
Increasing:
(-oo, 2)
Decreasing:
(2, oo)
Positive:
(0, 4)
Negative:
(-oo, 0), (4, oo)
Find the coordinates of the feasible region of the system below. Then, find the max and min values of the function for this region.
f(x, y) = 4x + 3y
x + y >= 2
4y <= x + 8
y >= 2x - 5
Vertices:
(0, 2), (4, 3), (7/3, -1/3)
Max: 25
Min: 6
The function below is vertically stretched by a factor of 2 and translated 3 units left, followed by a horizontal shrink by a factor of 1/3 and a translation 5 units down. Find this new function and name it h(x)
f(x) = 2x^2 - 3x + 1
h(x) = 36x^2 + 54x + 15
Write the following function as a piecewise function:
f(x) = -2abs(x - 5) + 3
y = -2x + 13; x > 5
y = 2x - 7, x <=5
Solve for x. Write your answer in interval notation:
6 - 5abs(7 + 5x)>=-109
[-6, 16/5]
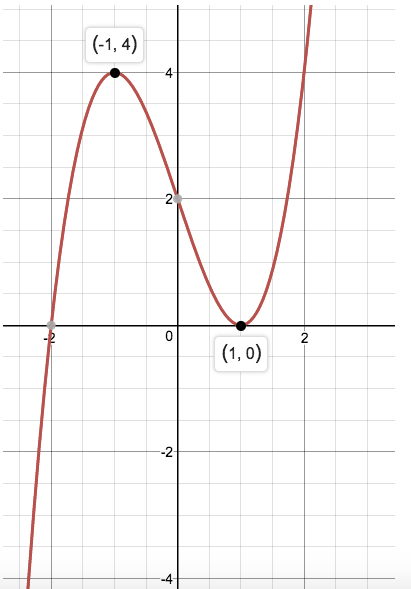
Sketch a graph with the following characteristics:
-only negative over the interval (-inf, -2)
only positive over the interval (-2, 1), (1, inf)
-increasing (-inf, -1), (1, inf)
A jewelry company makes and sells necklaces. For one type of necklace, the company uses clay and glass beads. Each necklace has no more than 10 clay beads and at least 4 glass beads. For every necklace, four times the number of glass beads is less than or equal to 8 more than twice the number of clay beads. Each clay bead costs $0.20 and each glass bead costs $0.40. Find the number of clay and glass beads the company should use in a necklace to minimize costs. Also, find the minimum cost
Minimum cost is $2.40 from 4 clay and 4 glass beads.