Unit 1
Unit 2
Unit 3
Unit 4
100
Create a function, f(x), that models the graph below.
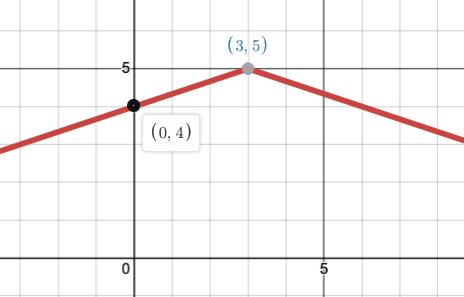
f(x) = -1/3abs(x - 3) + 5
100
Solve for x:
9x^2 + 6x - 16 = 7
x = (-1 +- 2sqrt6)/3
100
Create a polynomial function, in factored form, with the smallest possible degree. Assume the a-value is either 1 or -1.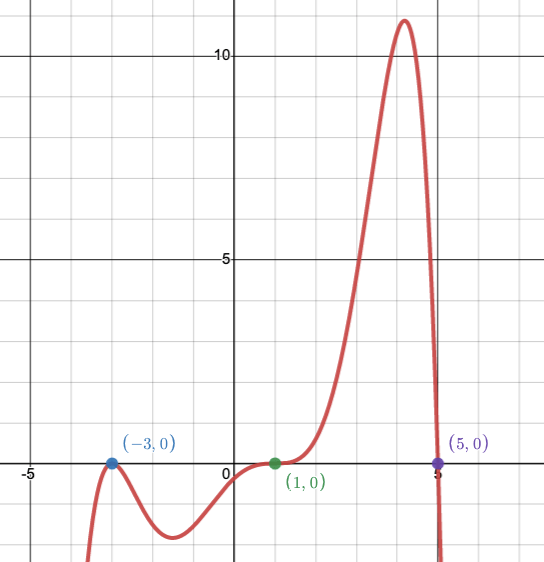
p(x) = -(x + 3)^2(x - 1)^3(x - 5)
100
Identify any asymptotes, intercepts, and/or holes of the following function:
f(x) = (x^3 - x^2 - 12x)/(-4x^2 + 12x)
Intercepts: (4, 0), (-3, 0)
Hole: (0, -1)
Asymptes: x = 3
y = -1/4x - 1/2
200
Describe the domain, range, interval(s) of increasing and interval(s) of decreasing in interval notation.
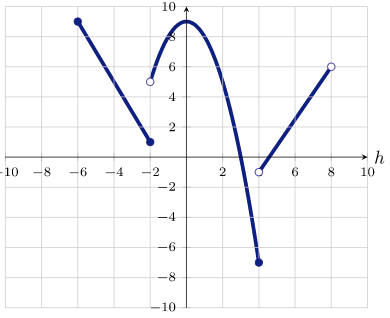
Domain: [-6, 8)
Range: [-7, 9]
Increasing: (-2, 0) U (4, 8)
Decreasing: (-6, -2) U (0, 4)
200
Find all possible solutions (real and imaginary):
9x^2 + 2x + 11 = -9x
x = (-11 +-5isqrt11)/18
200
Find all real and imaginary zeros:
y = x^3 - 3x^2 + x - 3
x = 3, +-i
200
Create an equation that models the function below.
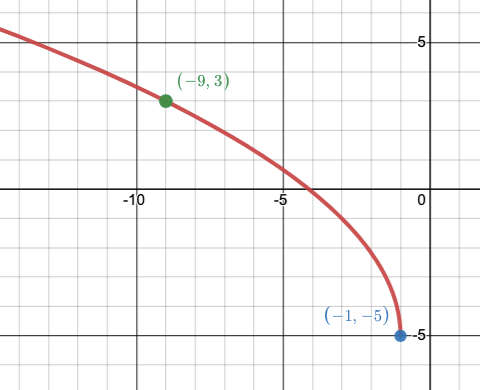
f(x) = 2sqrt(-2(x + 1)) - 5
300
Describe the transformations, using proper mathematical language, of f(x) if...
g(x) = 4/3f(-1/2x + 7) - 3
-vertical stretch by a factor of 4/3
-reflection over the y-axis
-horizontal stretch by a factor of 2
-translation right 14, down 3
300
Find the maximum or minimum value of the function below. Your answer should be a simplified fraction.
f(x) = -x^2 - 5x + 7
max value:
53/4
300
Find all real and imaginary roots of the following polynomial:
y = 8x^3 + 27
x = -3/2, (3 +-3isqrt3)/4
300
Simplify. List excluded values.
(6x^2 - 33x +15)/(2x^2 - 5x - 3) times (3 - x)/(x^3 + 5x^2 + x + 5) divide (2x^2 - 5x + 2)/(2x^2 + 15x + 7)
[-3(x + 7)(x - 5)]/[(x^2 + 1)(x - 2)(x + 5)
x!= 1/2, -1/2, 3, -5, -7, 1
400
What is the average rate of change of the function below over the interval [-1, 4]?
f(x) = -2x^2 + 5
-6
400
Simplify the following expression:
(-4i^34sqrt-9)(-5 - 2i)
24 - 60i
400
Find the 7th term of the binomial expansion of
(4x - 3)^9
3,919,104x^3
400
Solve.
5/(2-x) + (x - 5)/(x + 2) + (3x + 8)/(x^2 - 4) = 0
x = 1, 8
500
Consider these three coordinated from some function, f(x): (-2, 1), (3, -4), (7, 0)
Name three coordinates of g(x) be if ...
g(x) = -3/2f(5/2x - 15/2) + 5
(11/5, 7/2), (21/5, 11), (29/5, 5)
500
Rewrite the following equation in vertex form:
y = 4x^2 - 12x + 5
y = 4(x - 3/2)^2 - 4
500
Find all real and imaginary zeros of the function:
f(x) = x^5 -4x^4 + 4x^3 - 16x^2 + 3x - 12
x = 4, +-isqrt3, +-i
500
Simplify.
(1/(3a) - 1/(3b))/(a/b - b/a)
-1/(3(a + b))