How many different ways can you rearrange the letters in the word "ALGEBRA".
2520
What is the probability that the spinner lands on an even number or a 5? Write your answer as a simplified fraction.

3/5
Consider the two-way table below. If event A is viewing Version 2 and event B is Unlike to Buy, are event A and B independent or dependent events? Show how you know.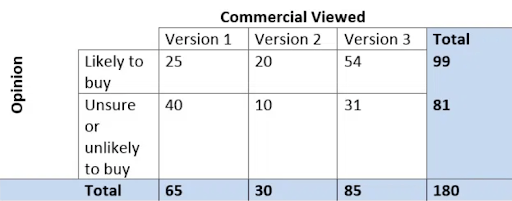
Dependent, work may vary
You are selling raffle tickets for a fundraiser. People can buy as many tickets as they want. One ticket is randomly selected to decide who gets a prize. Is this fair? Why?
yes, because each ticket has the same probability of getting picked
What percentage of data that is normally distributed falls within one standard deviation to the left of the mean and two to the right of the mean?
81.5%
What is the probability that you are dealt a 5-card poker hand that is all face cards? Write your answer as a decimal with four decimal places.
0.0003
What is the probability that the spinner below lands on a multiple of 3 or a number greater than 6?

1/2
Mrs. G.A. is picking names from her third period class from a hat. There are 22 freshmen and 11 sophomores in that period. She keeps picking names, without replacing them in the hat, until she picks a sophomore. What is the probability that she picks a sophomore on the fourth pick? Write your answer as a decimal rounded to the nearest thousandth.
0.103
Mrs. G.A. is running an illegal gambling ring out of her classroom during tutorial. In one game, you roll a six-sided die. If you roll a 6, you win $10, but if you roll anything else, you get nothing. It costs $2 to play. Is this a fair game? Explain why or why not.
No because the expected value is about $1.66 which is less than the cost to play.
Consider the following test scores: 45, 47, 48, 46, 45, 44, 50, 45, 46, 49, 43, 44. What is the mean, median, and IQR of this data? Round your answers to the nearest tenth, if necessary.
Mean: 46
Median: 45.5
IQR: 3
There are 18 girls and 15 boys in Mrs. G.A.'s 1st period class. She does a Unit Circle race to see who can fill out a unit circle the fastest, and is awarding first, second, and third place prizes. What is the probability that all three winners are girls? Write your answer as a simplified fraction.
51/341
You roll a twelve sided dice. What is the probability that you roll a prime number or a multiple of 6? Write you answer as a simplified fraction.
7/12
Consider the two way table below with data about the Titanic. Of the people who did not survive, what is the probability that they were a third class passenger? Of the people who were third class passengers, what is the probability that they did not survive? Write your answers as percentages to the nearest who number, in the correct order.
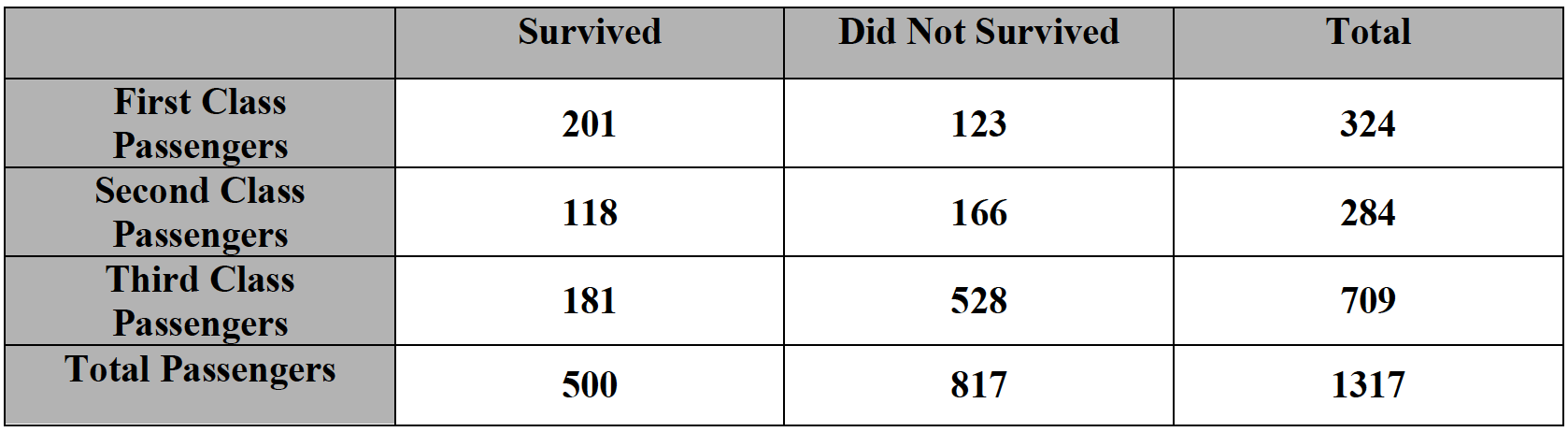
65%, 74%
Mrs. Frangieh has about a 66% chance of winning, so Mrs. G.A. should grade 99 finals and Mrs. Frangieh should grade 51 finals.
Consider the spinner. What is the probability that, if you spin it 5 times, it lands on grey 3 times? Write your answer as a simplified fraction.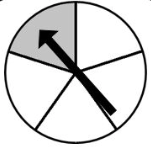
32/625
Mrs. Frangieh is hanging up the letters of the word PRECALCULUS on her wall. She is randomly picking the letters from a bag as she hangs them from left to right. What is the probability that, when she is done, the two C's are next to each other, the two L's are next to each other, and the two U's are next to each other? Write your answer as a simplified fraction.
4/495
You randomly pick a card from a standard deck. What is the probability that you pick a diamond or an odd number card or a card that is a multiple of 3? Write your answer as a simplified fraction.
7/13
75% of Algebra 2 Honors students sign up for Precalculus Honors rather than Precalculus. 33% of those PCH students went against their teacher recommendation for math course, while only 4% of the PC students went against their teacher recommendation. What is the probability that a student that went against their teacher recommendation is in PCH? Write your answer as a decimal rounded to the nearest hundredth.
0.96
Mrs. G.A. is running an illegal gambling ring out of her classroom during tutorial. In one game, you randomly pick two cards from a standard deck (without replacement). If you pick two cards of the same suit, you win $15. If you pick two cards of the same color but different suit, you win $5. If you pick two different colors you win nothing. What should the cost of the game be if Mrs. G.A. wants it to be a fair game?
$4.85
Mrs. G.A.'s Unit 9 Test is out of 50 points. The data is distributed normally. The mean score of that test is 42 and the standard deviation is 2.15. What percentage of the class received a B (between 80% and 90%)? Use the Standard Normal Table from your last homework worksheet.
74.3%
You are rolling four 6-sided dice. What is the probability that you roll at least 2 fours?
19/144
364 people were surveyed to see if they drank coffee or tea. It is possible that the people surveyed drink only coffee, only tea, both or neither. 187 people said they drink tea, 221 said they drink coffee, and 52 said they drink neither. What is the probability that a someone from the survey drinks coffee or tea? Write your answer as a simplified fraction
6/7
Mrs. G.A. teaches Algebra 2 Honors and Calculus. 68% of her students are in Algebra 2H. 91% of her Calculus students are passing the class, and 97% of her Algebra 2 Honors students are passing the class. A student comes in during tutorial, upset that they are failing. What is the probability that this is a 2H student? Write your answer as a percentage rounded to the nearest whole number.
41%
Scientists have developed a new test to test for Covid 23. In a study of 25000, 4% of participants actually had Covid 23. The test correctly identified 100% of those that actually had Covid 23, and correctly identified 95% of those that did not actually have Covid 23. If you tested positive for Covid 23 using this test, would you trust it? Justify your answer with math!
No because of those that tested positive for Covid 23, only about 45% actually had Covid 23.
Mrs. Frangieh decided to take the SAT for fun in 2022. The scores that year were normally distributed. The mean score that year was 1060 and the standard deviation was 195. If only 0.49% of the people that took the SAT scored higher than Mrs. Frangieh, what was her score? Round to the nearest whole number. Use the standard normal table from your last homework worksheet.
1563