Expressions, Functions, and Statistics & Probability
Linear Functions, Equations, & Inequalities
Quadratic Functions & Equations
Exponential Functions & Equations
200
Which expression is equivalent to
(5x^2+13.2x-15) + (4.8x-7.7) ?
A. 0.3x^2
B. 23x^2
C. 5x^2+18x-22.7
D. 9.8x^2+5.5x-15
C. 5x^2+18x-22.7
200
Vikram buys two sandwiches for s dollars each. He pays with a $10 bill. The cashier gives Vikram some money back as change.
Create an expression to model the amount that Vikram got back from the cashier.
10-2s
200
An equation is shown.
y=4x2-64
Select all of the zeros in the equation.
A. -8
B. -4
C. 0
D. 4
E. 8
B. -4
D. 4
200
Which situation could be best modeled by a linear function?
A. Reuben's car loses 1/20 of its value every year.
B. Every year, the number of chickens a farm has doubles.
C. Alia puts away ten dollars per month to save up for a new computer.
D. Claudia earns 3% interest on money in her bank account every year.
C. Alia puts away ten dollars per month to save up for a new computer.
200
A rectangle has a length of 3x^4 and a width of 5x-4 . Which expression represents the area of the rectangle?
A. 8x^5-4
B. 8x^5-7x^4
C. 15x^5-4
D. 15x^5-12x^4
D. 15x^5-12x^4
200
Amelia is entering an amusement park. The entrance fee is $12.50, and each ride costs $1.29. Amelia wants to spend at most $35.
Part A. Create an inequality to determine r, the number of rides Amelia could go on.
Part B. How many rides could Amelia go on?
Part A: 12.50+1.29r<=35
Part B: 17 rides
200
An equation is shown.
x2+12x+32=0
What are the solutions to the equation?
(2 solutions)
-4 and -8
200
Veronica has a bank account with $2000 in it. The formula A=2000(1+0.03)t shows how much money is in the account in t years. The annual interest rate is 3%. Veronica would like to know how much interest she gets every three months.
Which equation can be used to reveal the interest rate she gets every three months?
A. A=2000(1+0.03)t/3
B. A=2000((1+0.03)3)3t
C. A=2000(1+(0.03)1/4)4t
D. A=2000((1+0.03)1/4)4t
D. A=2000((1+0.03)1/4)4t
200
An equation is shown.
x^3=-8
What is the value of x?
x=-2
200
This item has two parts.
Vanessa incorrectly solves the equation 6(2x-8)+2=1/3(6x+12) .
Part A.
Select the first line in which Vanessa makes an error.
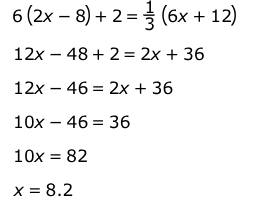
Part B.
Create a correct equation to replace the incorrect equation in part A.
Part A:
12x– 48 + 2 = 2x+36
Part B:
12x–48+2=2x+4
200
Two equivalent equations, where n represents a real number, are shown.
x^2-x/4+1/64=0
(x-n)^2=0
What is the value of n?
n=1/8 or 0.125
200
Gina has $2,000 in the bank. The interest rate is 3% per year. She does not add any more money in the account.
Let y be the number of years the money is in the bank.
Which equation can be used to find the number of years it will take to have $3,200 in the account?
A. 3,200=2,000+2,000(1.03)y
B. 3,200=2,000y1.03
C. 3,200=2,000·(1.03)y
D. 3,200=2,000(.97)y
C. 3,200=2,000·(1.03)y
200
An expression is shown.
72x^3y^2-24x^2y^6
Beth rewrites the expression as the product of 24x^2y^2 and a binomial.
Which expression represents the binomial?
A. 3x-1
B. 3x-y^4
C. 48x-y^4
D. 3x-24x^2y^6
B. 3x-y^4
200
Emma went to the store on Monday and Friday.
- On Monday, she bought 8 ounces of almonds and 20 dollars of other food.
- On Friday, she bought 40 ounces of almonds and 4 dollars of other food.
- Emma spent more on Friday than she did on Monday.
Let s be the cost per ounce, in dollars, of almonds.
Create an inequality that models this situation.
8s+20<40s+4
200
Desiree tossed a ball in the air. The function modeling the height of the ball after t seconds is shown.
h(t)=-16t2+30t+4
What is the domain for this situation?
____ ≤t≤____
0≤t≤2
200
Select all of the following sets that represent a function.
A. {(4,7), (5,10), (6,7), (7,7)}
B. {(3,3), (4,3), (8,2), (9, 10)}
C. {(3,3), (3,4), (4,5), (5,6)}
D. {(7,7), (8,7), (9,9), (10,1)}
A. {(4,7), (5,10), (6,7), (7,7)}
B. {(3,3), (4,3), (8,2), (9, 10)}
D. {(7,7), (8,7), (9,9), (10,1)}
200
At an arcade, a player starts with a number of tokens, t, and spends 3 tokens per round in a game. A recursive formula modeling the number of tokens remaining after n rounds is shown.
f(0)=t
f(n)=f(n-1)-3
Create an explicit formula g(n) that could also model the situation for n≥0.
g(n)=____________________
g(n)=t-3n
200
The function f(x)=2x-3 is shown on the graph.
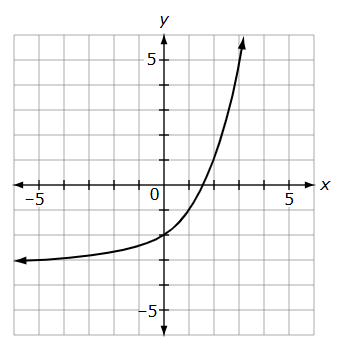
Complete the statement to describe the end behavior of the function.
As x approaches - ∞, the values of f(x) approach __________
As x approaches + ∞, the values of f(x) approach ___________
-3 and +∞
200
Which mapping represents a relation that is a function?
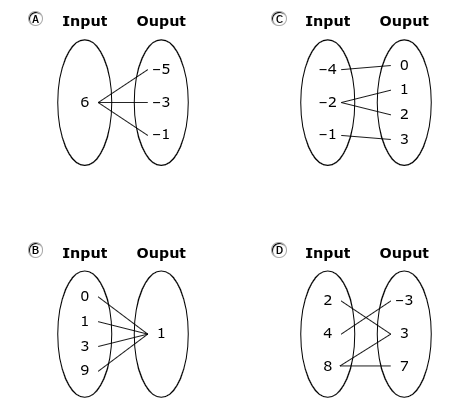
B
200
A sequence is defined by the formula shown, where an represents the nth term of the sequence and n≥1.
an+1=an-8
Which statement shows how to calculate the fifth term of the sequence?
A. a4=a5-8
B. a5=a4-8
C. a5=a6-8
D. a6=a5-8
B.
200
The graph of a function is shown.
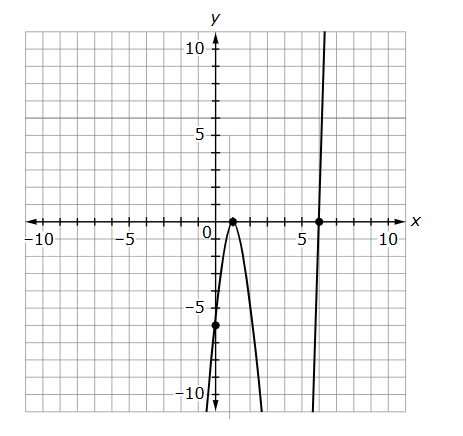
Select all of the zeros of the function.
A. -6
B. -1
C. 0
D. 1
E. 6
D. 1
E. 6
200
A bicycle shop has a volunteer program. Each volunteer will repair 2 bicycles. The equation shown represents the number of bicycles the shop has repaired since the volunteer program began. Let x be the number of volunteers.
f(x)=2x+15
Which set of values is in the domain of the function f ?
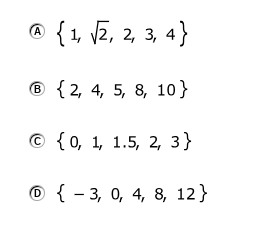
B. {2, 4, 5, 8, 10}
200
An inequality is shown.
18x-8>4x+8
Solve for x.
x=8/7
200
A function is shown on the graph.
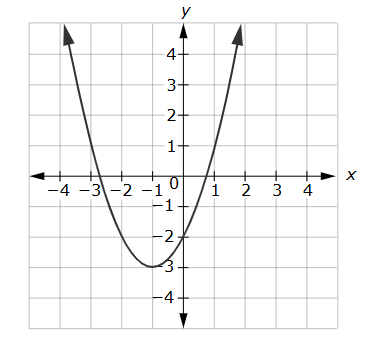
What is the line of symmetry?
x=-1
200
This question has two parts.
Two functions are shown.
f(x)=x^3-9x
g(x)=4x+12
Part A. Complete the table of values for the two functions.
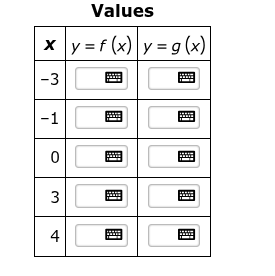
Part B. Select all of the solutions to f(x)=g(x) .
A. -3
B. -1
C. 0
D. 3
E. 4
F. None of these values are solutions.
Part A:
Part B:
A. -3, B. -1, and E. 4
200
An equation is shown.
742-x+18=2/3x+15
What is the value of x?
x=447
200
An equation is shown.
y=-x2+8x-15
What is the maximum value y can have?
1
200
A scientist measures the amount of bacteria in a petri dish. The amount of the bacteria in the petri dish can be modeled by the function G(t)=350(1.048)^t , where t represents the time, in hours, since the scientist began measuring the amount of bacteria.
How many bacteria are in the petri dish after 6 hours? Round your answer to the nearest integer.
464 bacteria are in the petri dish after 6 hours.
200
An inequality is shown.
4x+20<12
Solve for x.
A. x<-17
B. x<-2
C. x<8
D. x<23
B. x<-2
200
A function is shown.
f(x)=x3+8x2-9x
Plot the zeros of the function.
Points should be plotted on the x-axis at -9, 0, and 1.
200
Two local coffee shops record the amount of coffee they sell each day for one month. The number of gallons of coffee sold per day for each shop is shown in the box plots.
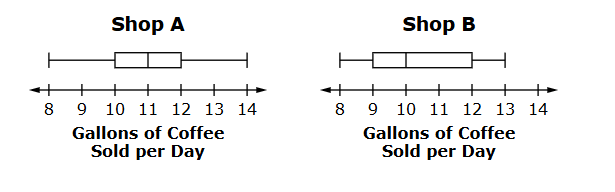
Select all of the true statements.
A. The data set for Shop A is skewed.
B. The data set for Shop B is skewed.
C. The mean of Shop A is greater than the median of Shop B.
D. The mean of Shop B is greater than the median of Shop B.
E. The middle 50% of data has a higher spread for Shop A than for Shop B.
B, C, and D
200
A fish jumps out of a lake into the air and then back into the lake. The jump could be graphed on a coordinate plane where x represents time and y represents the distance above or below the surface of the lake.
Which set of values would best represent the domain for this graph?
A. integers
B. positive integers
C. real numbers
D. positive real numbers
D. positive real numbers
200
Two clubs sell boxes of candy as a fundraiser for several days. The numbers of boxes sold per day by the members of each club are shown on the two dot plots.
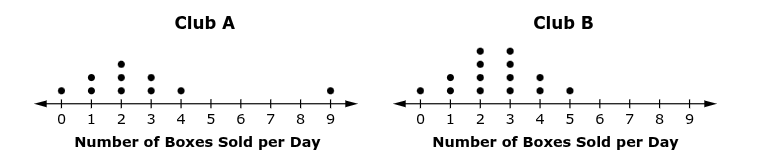
The outlier is removed from the data set for Club A.
Select all of the true statements, given that the outlier is removed.
A. The data set for Club A is symmetric.
B. The data set for Club B is symmetric.
C. The median of Club A is equal to the mean of Club B.
D. The range of Club A is greater than the range of Club B.
E. The IQR of Club A is less than the IQR of Club B.
A and B
200
Monique makes 100 necklaces to sell at a craft fair. She uses the function f(x)=22.50x-342 to model her profits, where x is the number of necklaces she sells at the craft fair.
Which set of values represents the domain of the function?
A. all integers from -342 to 100
B. all whole numbers from 0 to 100
C. all real numbers from 15.2 to 100
D. all real numbers from -342 to 1908
B. all whole numbers from 0 to 100
200
Demarco asks students in his English class whether they prefer to read fiction or nonfiction books. Some results of his survey are shown in the table.
Which statement is true based on the frequency table?
A. Most students in the class prefer nonfiction.
B. A student is more likely to prefer fiction if he or she is a sophomore.
C. A student is more likely to be a freshman if he or she prefers fiction.
D. A student is more likely to prefer nonfiction if he or she is a freshman.
C. A student is more likely to be a freshman if he or she prefers fiction.
200
Lenny rents a truck from a company. The first 4 hours are included in the initial fee, but he pays for any hours over 4, rounded up to the next hour. The function shown represents the cost, in dollars, when Lenny rents the truck for over h hours.
c(h)=18(h-4)+50
What does the 18 represent in this situation?
A. the cost per hour after the initial 4 hours
B. the total number of hours Lenny rents the truck
C. the initial fee Lenny pays, including the 4 hours
D. the hourly cost of renting the truck for time over 4 hours
A. the cost per hour after the initial 4 hours
200
This item has two parts.
A local library has a computer club with 25 members. The library surveys the members on whether they have a laptop or desktop computer at home.
- 7 members have a desktop computer at home.
- 3 members have a laptop computer and a desktop computer at home.
- All members have at least one type of computer at home.
Part A.
Enter a number in each box to complete the two-way frequency table.
Part B.
What is the probability that a randomly selected member has a laptop computer at home?
What fraction of members who have a laptop computer at home also have a desktop computer at home?
Part B
21/25
3/21 = 1/7
200
Rodney cleans houses to earn money. He charges the same amount for each house he cleans. The table shows the profit Rodney earns after cleaning certain numbers of houses and paying for his cleaning supplies.
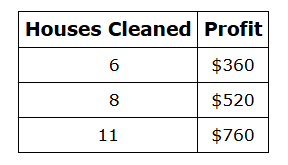
This item has two parts.
Rodney models the relationship between the number of houses and his profit using a linear function.
Part A.
What does the x-intercept of Rodney’s function represent?
A. the total number of houses Rodney cleaned
B. the amount of money Rodney spent on cleaning supplies
C. the amount of money that Rodney charges to clean one house
D. the number of houses Rodney cleaned to pay for his cleaning supplies
Part B.
What is the x-intercept of Rodney’s linear function?
Part A: D. the number of houses Rodney cleaned to pay for his cleaning supplies
Part B: 1.5
200
Which table of values represents a linear function?
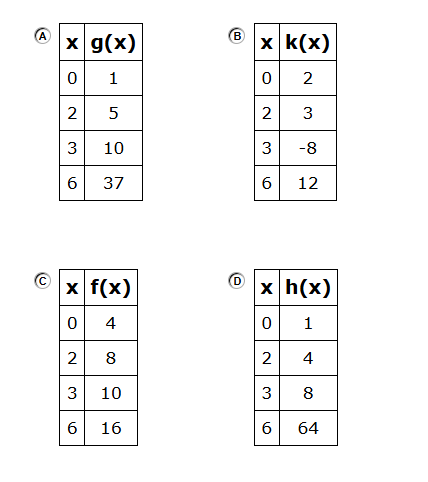
C.
200
An equation is shown.
y=2x+7
What is one solution to the equation?
x=_____
y=_____
Answers may vary.
Sample answer:
x=1
y=9