If, y=a(bx ), what do they represent?
a = initial amount/y-intercept
b = growth/decay factor
How do I know if an exponential function is exponential decay from an equation?
If the b is less than 1.
A bunny population doubles every 6 months. If the starting population is 10, how many will you have after 3 years? What is the initial population? What is the growth factor?
after 3 years = 640
initial population = 10
growth rate = 2
What is the percent growth/decay rate?
y=5(0.5)^x
decay by 50%
What is the initial value and growth/decay factor for the function f(x) = 2(3)x
**Make sure to identify whether it is growing or decaying**
initial value = 2
GROWTH FACTOR = 3
What percentage growth does this equation represent?
y = 3(1.5)x
50%
In exponential functions, when b>1 this will cause an exponential growth or decay?
Exponential growth
What is the percent growth/decay rate?
y=5(1.3)^x
growth by 30%
What is the equation for this exponential function.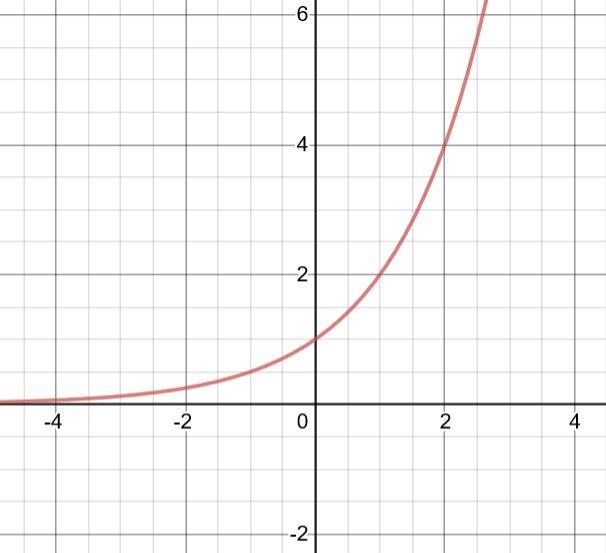
y = 1(2)x
f(x)=a(.93)x
Does this functions represent exponential growth or decay? What is the percent growth/decay rate?
Exponential Decay by 7%
f(x)=a(1.07)x
Does this functions represent exponential growth or decay? What's the percent growth/decay rate?
Exponential Growth. 7%.
What is the percent growth/decay rate?
y=(0.01)^x
decay by 99%
What is the equation for the function?
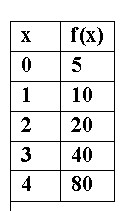
y = 5(2)x
What percentage growth does the following equation represent?
y = 4(3)x
200%
Does the graph represent exponential growth or decay?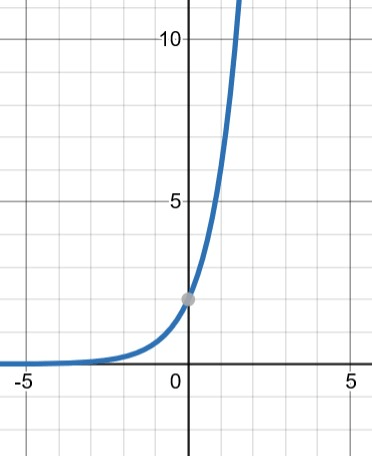
Exponential Growth
Is this exponential growth or decay?
What is the percent growth/decay rate?
y=1/2(0.7)^x
Decay by 30%
What is the difference between linear functions and exponential functions?
Linear has a constant rate of change (slope).
Exponential functions increase or decrease at an increasing rate (exponentially).
Ms. Wiggins purchased a car for 26,400 and every year it decays by 12%. What can she expect the value of her car to be after 3.5 years?
f(x) = 26400(.88)3.5 = $16,876.92
Annual sales of a fast food restaurant are $530,000 and increasing at a rate of 5%. What will the annual sales be in 6 years?
530,000(1.05)6 =$710,250.69
What is the percent growth/decay rate?
y=60(1.33)^x
growth by 33%