Variation Equations
Fundamental Theorem of Variation
Random
Fitting a model
The Graphs
100
y varies directly as the third power of x
y=kx^3
100
Suppose that a varies directly as the fourth power of b. How does the value of a change if
b is doubled
a is multiplied by
2^4 = 16
100
Consider the equation y=-2x^2 . Find the rate of change between x = 4 and x = 6.
-20
100
Consider the data below:
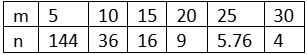
n varies ______________________ with the _____________ power of m
inversely; second
100
Which graphs have exactly one line of symmetry?
y=kx, y=kx^2,y=k/x,y=k/x^2
all but y=k/x
200
The area A of a regular hexagon is directly proportional to the square of the length s of a side.
A=ks^2
200
Suppose that a varies directly as the fourth power of b. How does the value of a change if
b is divided by 4
a is divided by 4^4=256
200
The number n of rubber balls that fit into a box varies inversely as the cube of the diameter d of each ball. A box that holds 12 balls with diameter 15 cm holds how many balls with diameter 5 cm?
n=k/d^3
12=k/15^3, k = 40,500
(40,500)/5^3=324
200
Write a general variation equation for the situation.
y=k/x
200
Which graphs have two lines of symmetry?
y=k/x
300
e is inversely proportional to the cube of g
e=k/(g^3)
300
Suppose that a varies directly as the fourth power of b. How does the value of a change if
b is multiplied by 1/4
a is multiplied by 1/256
300
The amount of electric power generated by a windmill varies directly as the cube of the wind speed. A particular windmill generates 640 watts of power when the wind is 8 miles per hour. Find the constant of variation and use it to write a variation formula. How much power will the windmill generate in a 12 mile per hour wind?
k = 1.25, E=1.25s^3 , 2,160 watts
300
Find the value of the constant of variation and rewrite the variation equation.
k = 1890
y=(1,890)/x
300
Which graphs have asymptotes?
y=kx, y=kx^2,y=k/x,y=k/x^2
y=k/x,y=k/x^2
400
A varies jointly as b, c, and the fourth power of d
A = kbcd^4
400
Suppose that p varies inversely as the fifth power of n. How does the value of p change if
n is divided by 5
p is multiplied by 5^5 = 3,125
400
Write an equation of a hyperbola that has points in the second quadrant.
y=-5/x
400
Students in a physics class tied a weight to a string and twirled it around a circle. The measured the length l of the string, the speed s, and the tension t in the string and collected the data in the tables below. 1) Does the tension vary with speed or with the square of speed? 2) Does the tension vary with length or with the square of length? 3) Write a variation equation relating t, s, and l. Do NOT solve for the constant.
1) square of speed
2) length
3) t=(ks^2)/l
400
When k<0, which graphs have points in the fourth quadrant?
y=kx, y=kx^2,y=k/x,y=k/x^2
all of the graphs
500
P varies inversely as the square of M and directly as R and as the cube of J. When R = 180, J = 2.1, and M = 19.4, P = 12.0. Find P when R = 144, J = 2.6, and M = 18.2.
20.6
500
Suppose that p varies inversely as the fifth power of n. How does the value of p change if
n is multiplied by 1/4
p is divided by (1/4)^5 = 1/1024
or p is multiplied by 1,024
500
When k<0, which graphs have some points in the first quadrant?
y=kx, y=kx^2,y=k/x,y=k/x^2
no graphs
500
How many pounds of force would be needed to loosen the same bolt with a 21-inch wrench?
90 lb
500
Which graphs are hyperbolas and which have branches?
y=k/x,y=k/x^2 they both have branches, only the first is a hyperbola