General Sequences and Series
Arithmetic Sequences
Geometric Sequences
Arithmetic Series
Geometric Series
100
What is the difference between a sequence and a series?
A sequence is an ordered list of numbers, whereas a series is the sum of a given number of terms in a sequence.
100
Given that a1 = 7 and an = an-1 - 3, find a6.
a6 = -8
100
For the given sequence, find the common ratio and the 9th term:
1/2, 2, 8, ...
r = 4
a12 = 32,768
100
Find S9 (Note: NOT t9)
13, 15, 17, ...
S9 = 189
100
Find S7 for the following sequence:
-2, -12, -72, ...
S7 = -3110
200
What is the difference between an arithmetic and a geometric sequence?
An arithmetic sequence is a sequence that has a common difference (the same number gets added each time).
A geometric sequence is a sequence that has a common ratio (the same number gets multiplied each time).
200
For the given sequence, find the common difference and the 10th term.
9, 12, 15, 18, ...
d = 3
a10 = 36
200
Given that a1 = -5 and an = 2an-1, find a6.
a6 = -160
200
Evaluate the given series.
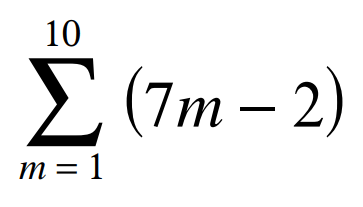
S10 = 365
200
Evaluate the given series:
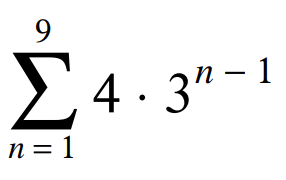
S9 = 39,364
300
Given a1 = 2 and an = 4an-1 + 1, find a5.
a5 = 597
300
Find three arithmetic means between -3 and 29.
-3, __, __, __, 29
5, 13, 21
300
Find two geometric means between 6 and 162.
6, __, __, 162
18, 54
300
Evaluate the following arithmetic series:
t1 = 42, t14 = 146
1316
300
Find the infinite sum, if possible.
1 + 0.5 + 0.25 + ...
2
400
There are 130 students in grade 1, 210 students in grade 2, and 290 students in grade 3 in a primary school, and so on in an arithmetic sequence. What's the total amount of students in the school? (there are 6 grades in the school).
1980 students
400
Given the explicit formula below, find the first four terms and a15.
an = -11+(n-1)7
-11, -4, 3, 10
a15 = 87
400
Given the explicit formula below, find the first four terms and a10 (round to nearest thousandth).
an = (1200)(1/2)n-1
1200, 600, 300, 150
a10 = 2.344
400
Determine the number of terms in the arithmetic series:
-1 + 2 + 5 + ... + 68
n = 24
400
Find the infinite sum, if possible.
a1 = -3, r=4
No sum (diverges)