Factor:
4x^2+4x
4x(x+1)
Given the general form of the reciprocal function, what information do the a, h, and k tell us?
y=a/(x-h)+k
a: stretch/compression/reflection
h: shift L or R
K: shift up or down
To add or subtract rational expressions, you need a __________ __________.
common denominator
What strategy can you use to divide rational expressions?
“keep, change, flip”
(multiply by the reciprocal)
Excluded values of a rational expression will make the value of the denominator equal to _____.
0
Factor:
x^2-25
(x+5)(x-5)
This is the name for a line that a function approaches but never actually touches.
Asymptote
Add the rational expressions and simplify your answer:
5/(14x) + 3/(2x)
13/(7x)
TRUE OR FALSE:
When multiplying or dividing a rational expression, you do NOT need a common denominator.
TRUE
Solve the rational equation (and check for extraneous solutions):
(x+3)/5 = (x+1)/2
x=1/3
Factor:
x^2+13x+42
(x+6)(x+7)
In the rational function:
y=-2/(x-1)+2
State the transformations.
Right 1
Stretched by 2 and reflected
Up 2
Find the common denominator of the rational expressions:
(2p)/(p+6) and 2/(5p-4)
(5p-4)(p+6)
Multiply the rational expressions:
1/(n+5) * (9n+45)/(n+5)
9/(n+5)
FREE POINTS!
+300
HOORAY!
Factor:
2x^2-2
2(x+1)(x-1)
Write the equations for the vertical and horizontal asymptotes of the following function:
y=1/(x-3)-1
VA: x=3
HA: y=-1
Subtract the rational expression:
4/(v+4) -3/4
(4-3v)/(4(v+4)
Divide the rational expressions:
(x-8)/(7x+14) div 1/(x+2)
(x-8)/7
Solve the rational equation (and check for extraneous solutions):
8/(x+3) = (x+1)/(x+6)
x=9,-5
Factor:
6x^2+10x-4
2(3x-1)(x+2)
Write the function represented by this graph:
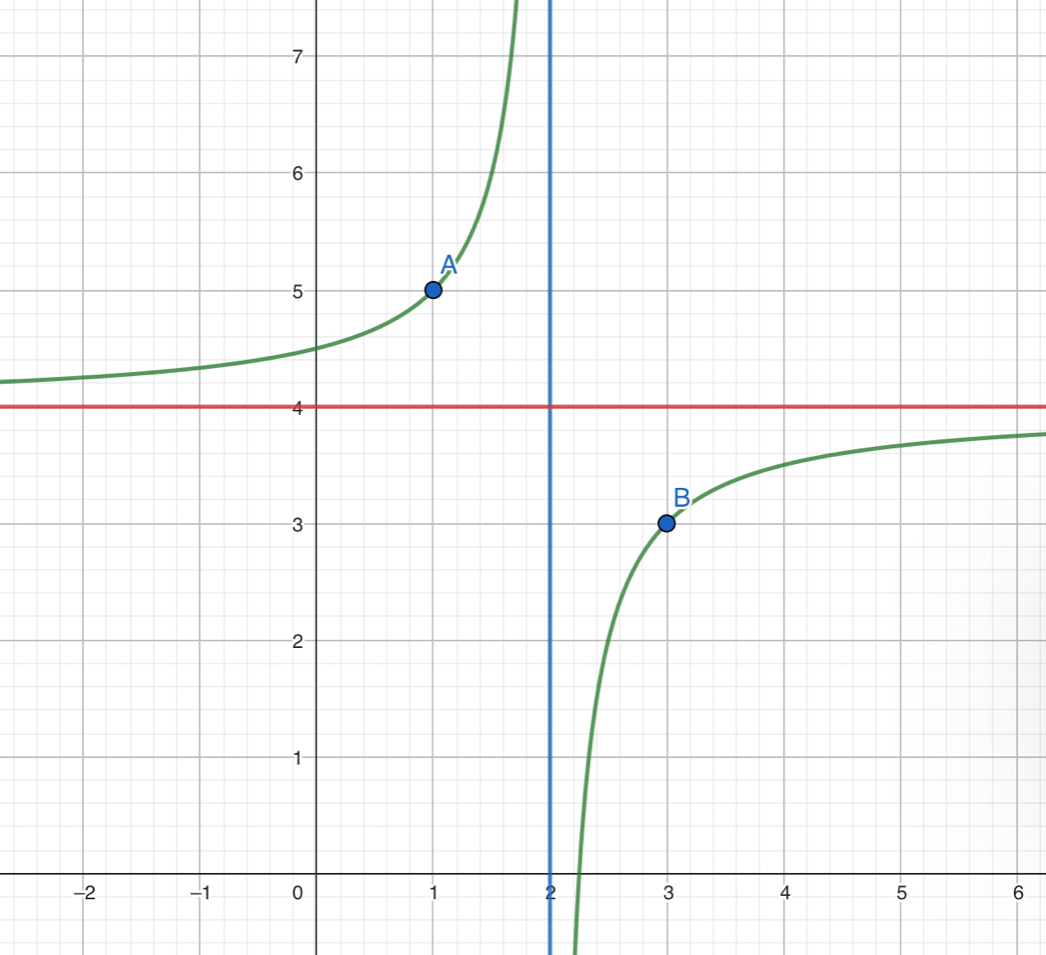
F(x)=-1/(x-2)+4
Add the rational expressions:
4/(3x+3)+1/(x-2)
(7x-5)/((3x+3)(x-2))
Multiply the rational expression:
(x+1)/(x^2-x-6) * (x^2+4x+4)/(x^2-4)
(x+1)/((x-3)(x-2))
Solve the rational equation (and check for extraneous solutions):
1/x+3/(x-4) = (2x+8)/(x^2-4x)
x=6