Name That Pair
Solve for X
Congruent or Supplementary?
Mystery Angle
Vocabulary & Proof
100
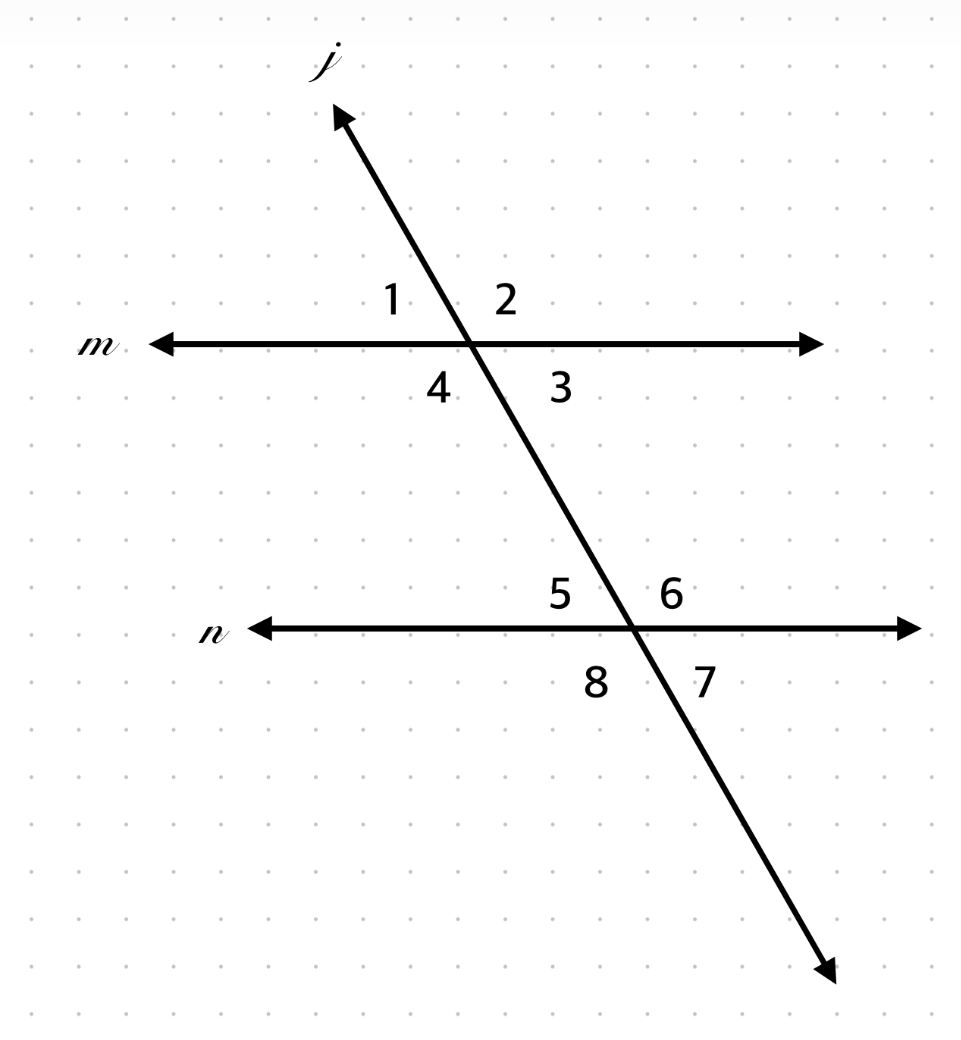
∠1 and ∠5 are what type of angles?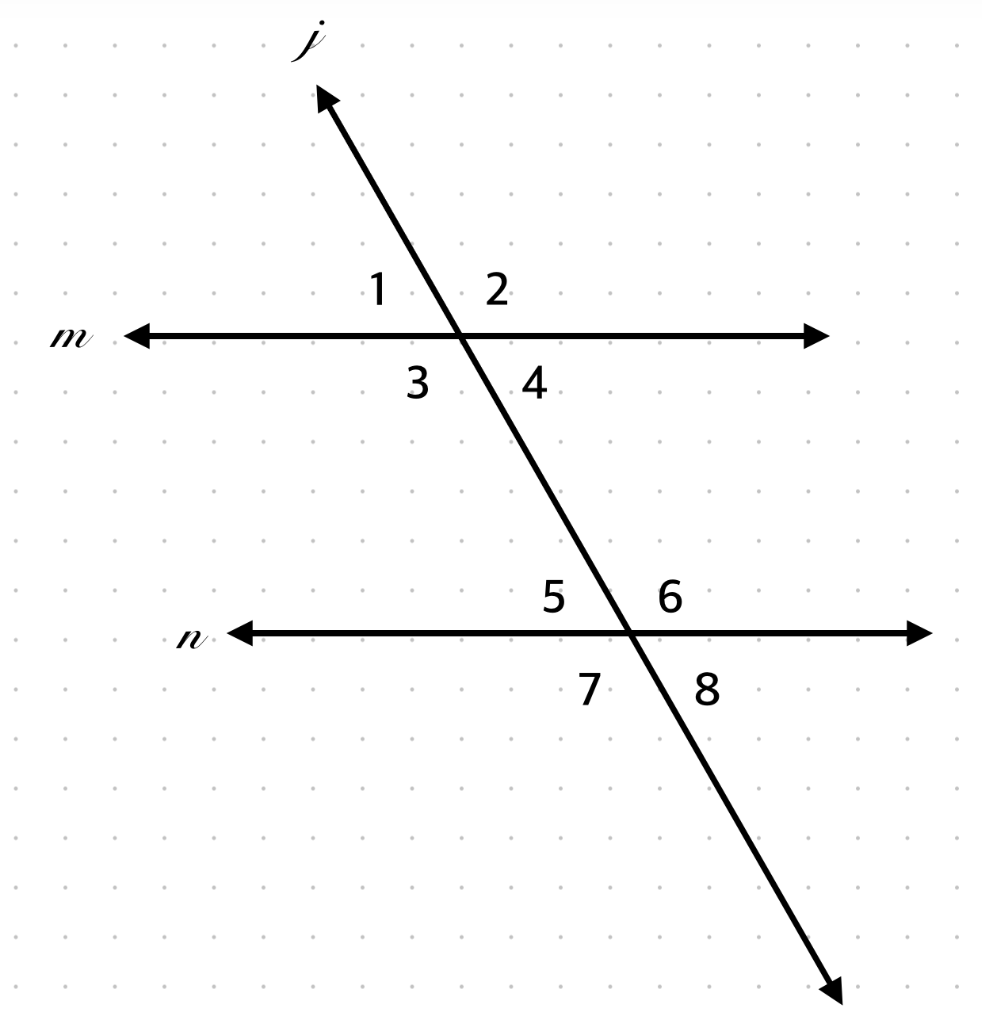
Corresponding Angles
100
If ∠1 = (2x + 10)° and ∠5 = (50)°, find x.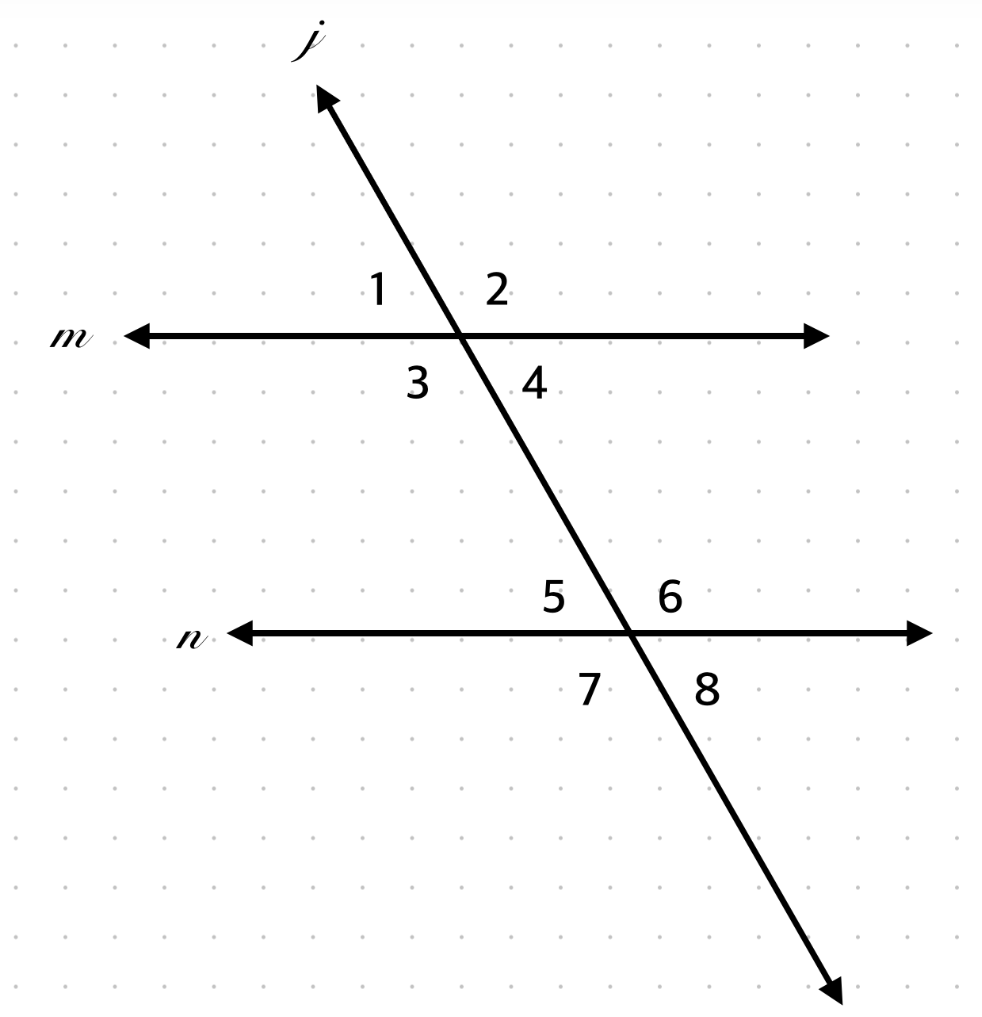
Corresponding → 2x + 10 = 50 → x = 20
100
∠1 and ∠7?
Congruent, alternate exterior
100
If ∠1 = 70°, what is ∠5?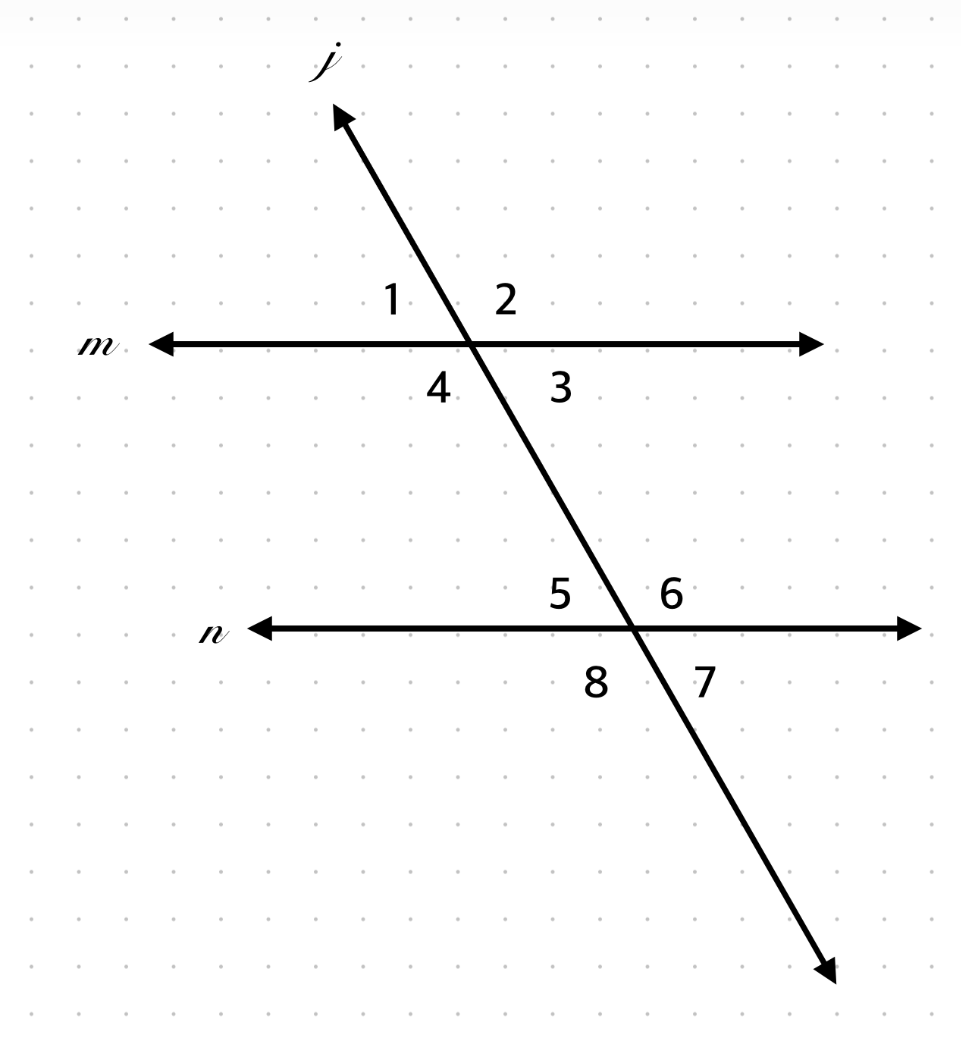
70°, corresponding
100
Define “transversal” and give an example in your own words.
A line that intersects two or more lines.
200
∠4 and ∠5 are what type of angles?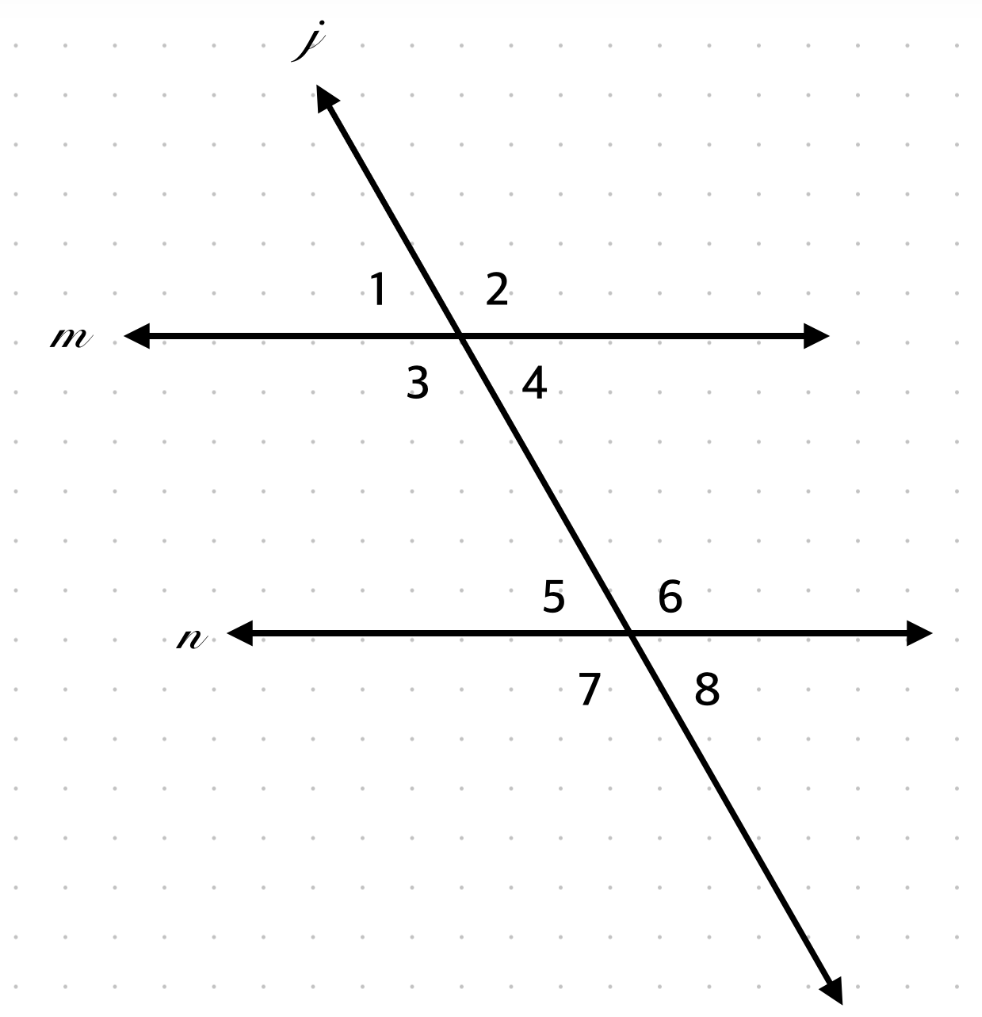
Alternate Interior Angles
200
If ∠3 = (5x – 15)° and ∠6 = (3x + 25)°, find x.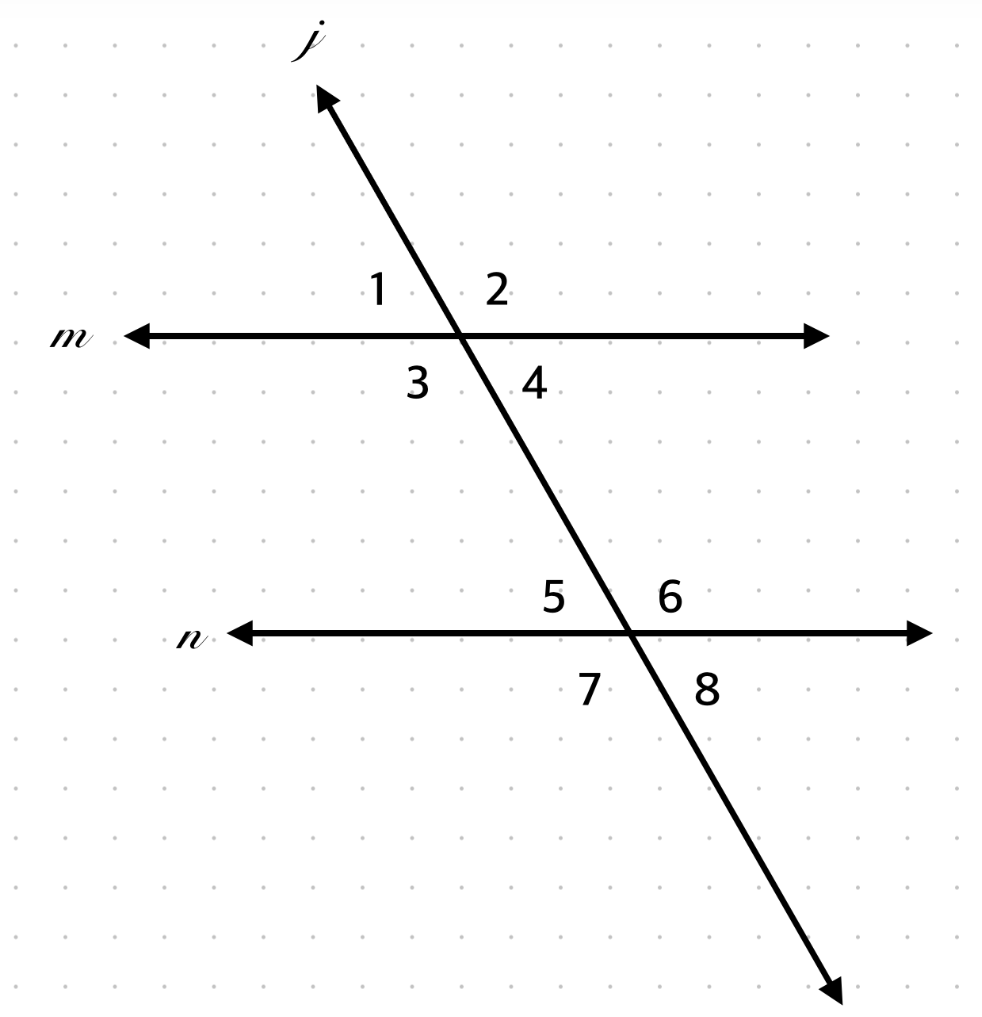
Alternate interior → 5x – 15 = 3x + 25 → x = 20
200
∠4 and ∠6?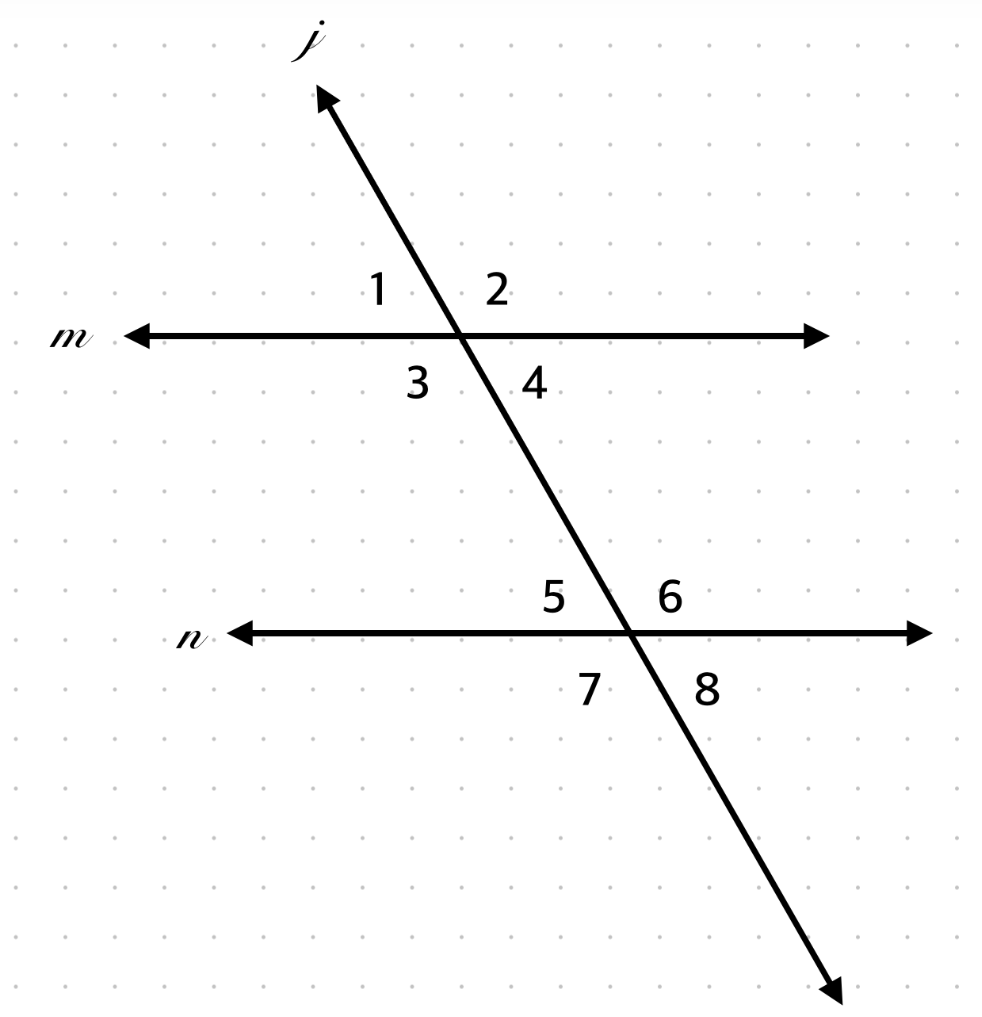
Supplementary, same-side interior
200
If ∠4 = 120°, what is ∠6?
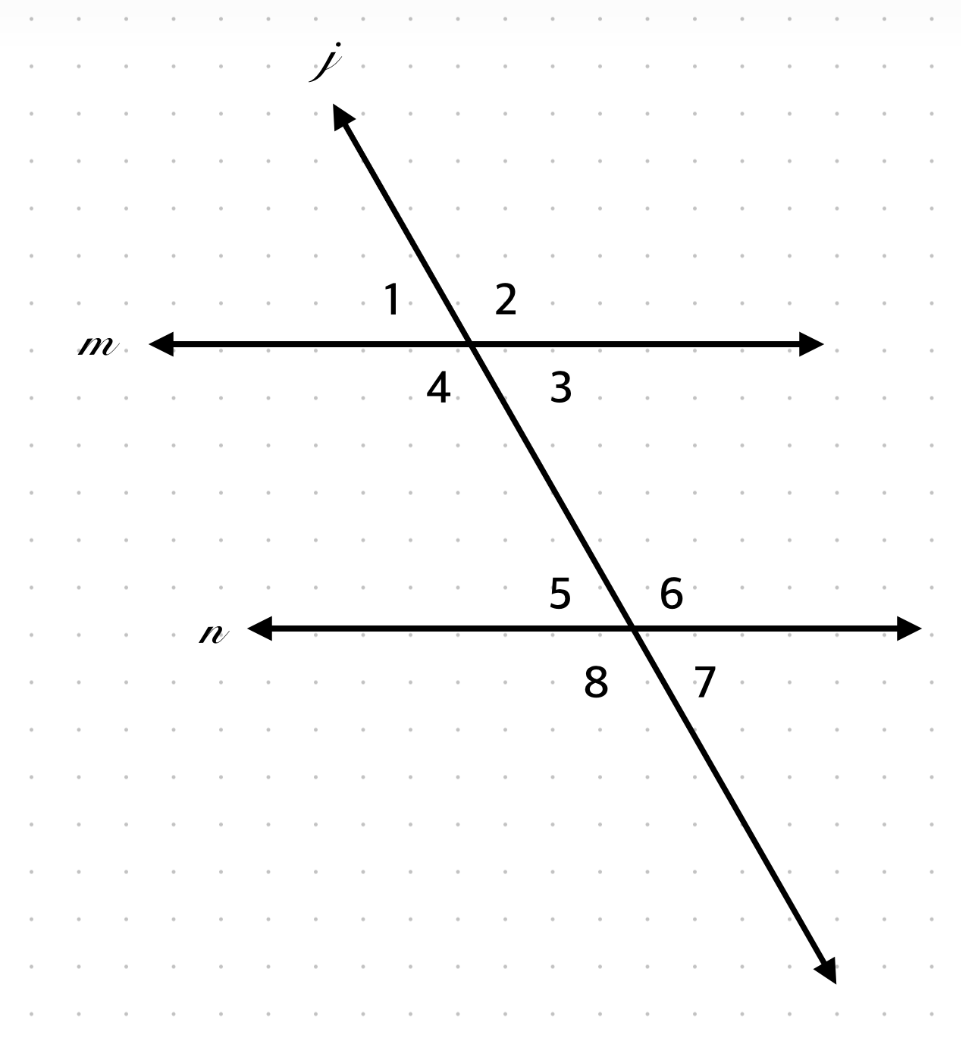
120°, alternate interior
200
State the theorem for alternate interior angles with parallel lines.
They are congruent.
300
∠3 and ∠7 are what type of angles?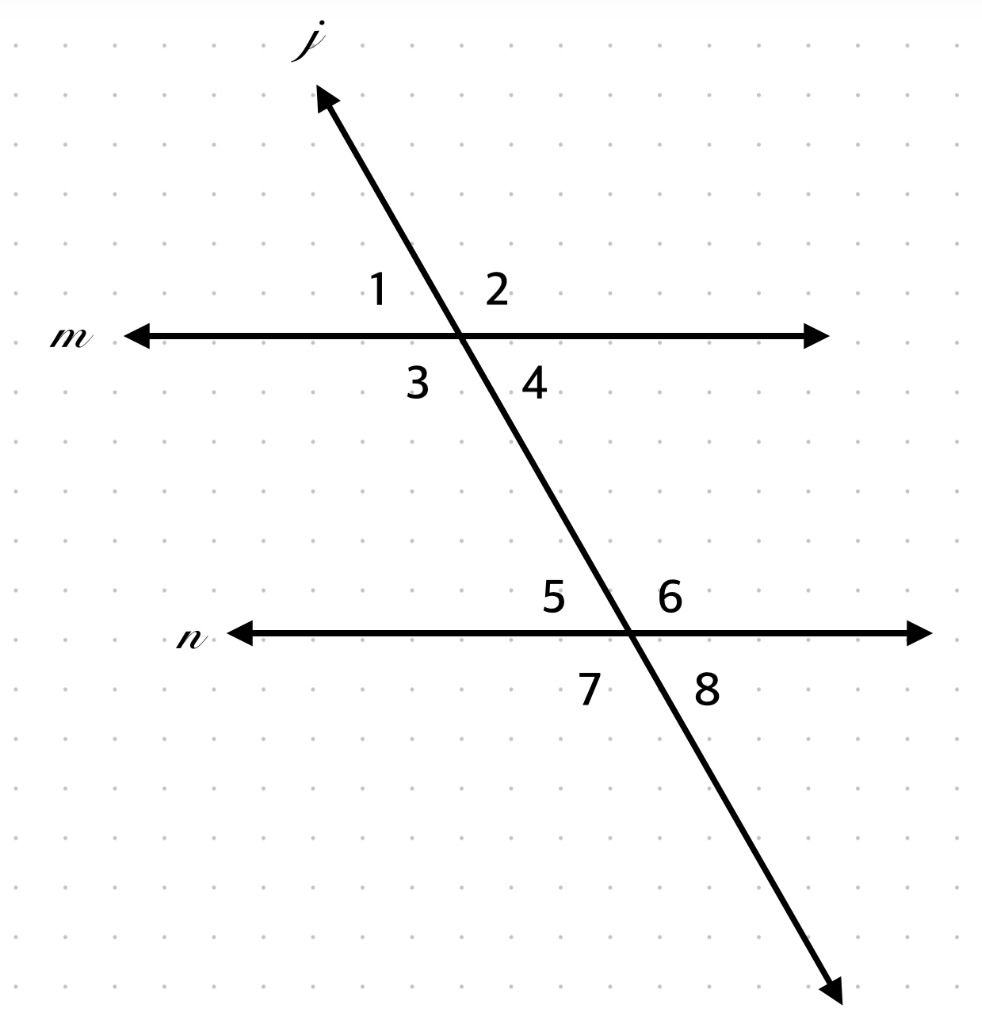
Alternate Exterior Angles
300
If ∠2 = (7x + 5)° and ∠3 = (9x – 15)°, find x.
Linear pair → add to 180 → 7x + 5 + 9x – 15 = 180 → x = 11
300
∠1 and ∠7?
Congruent, alternate exterior
300
If ∠3 = 110°, what is ∠4?
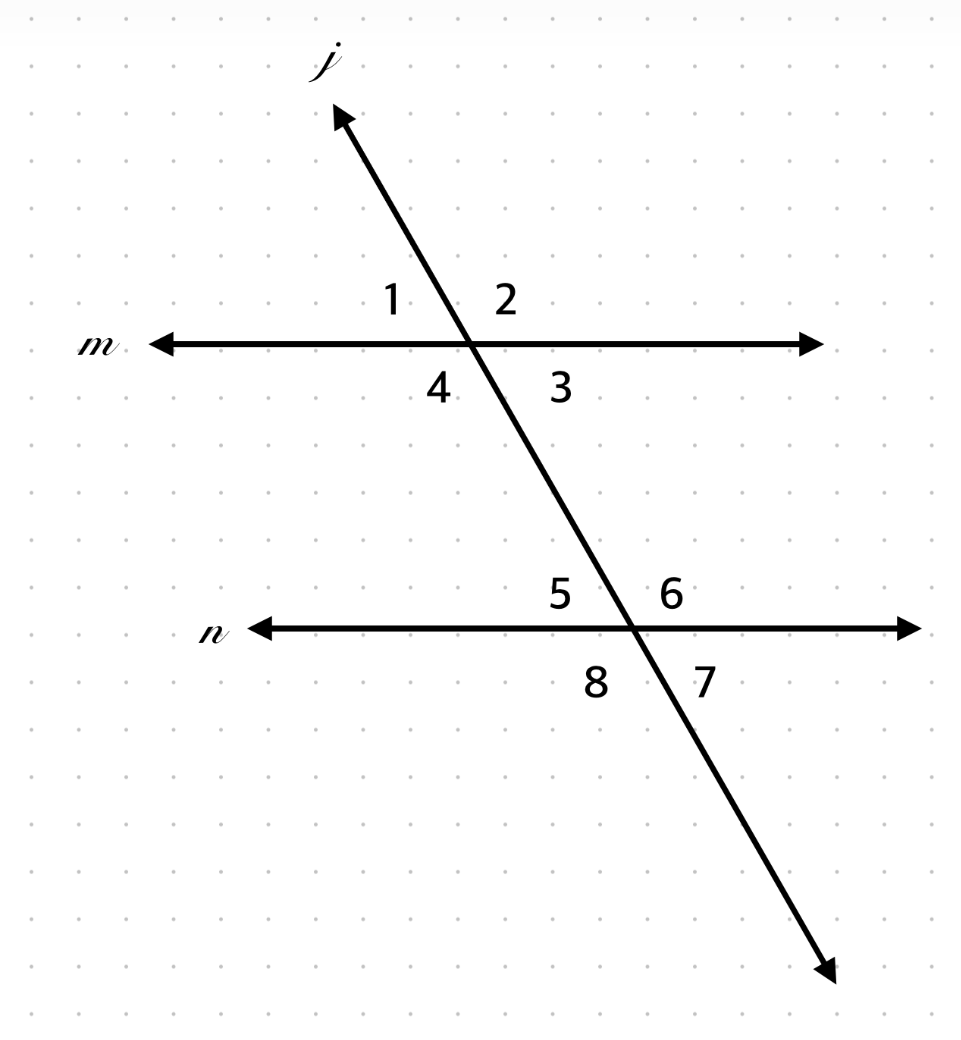
70°, supplementary linear pair
300
Why are ∠2 and ∠3 supplementary?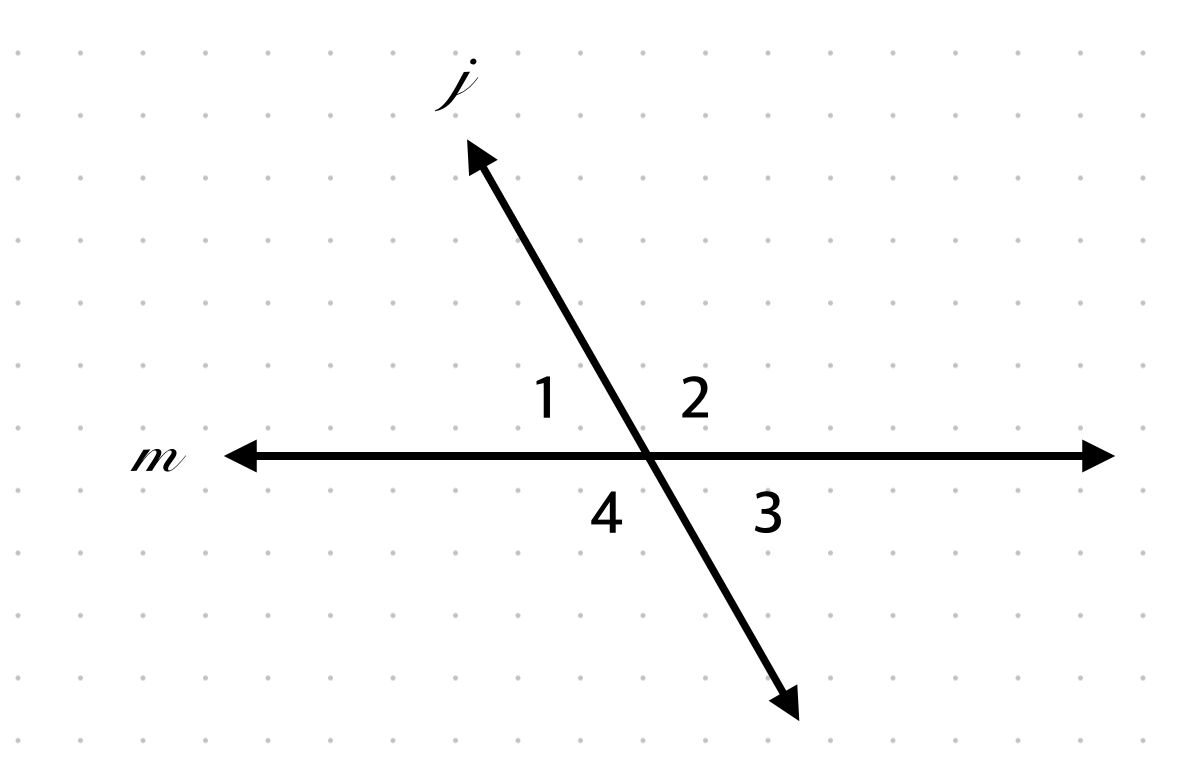
(They form a linear pair)
400
∠2 and ∠3 are what type of angles?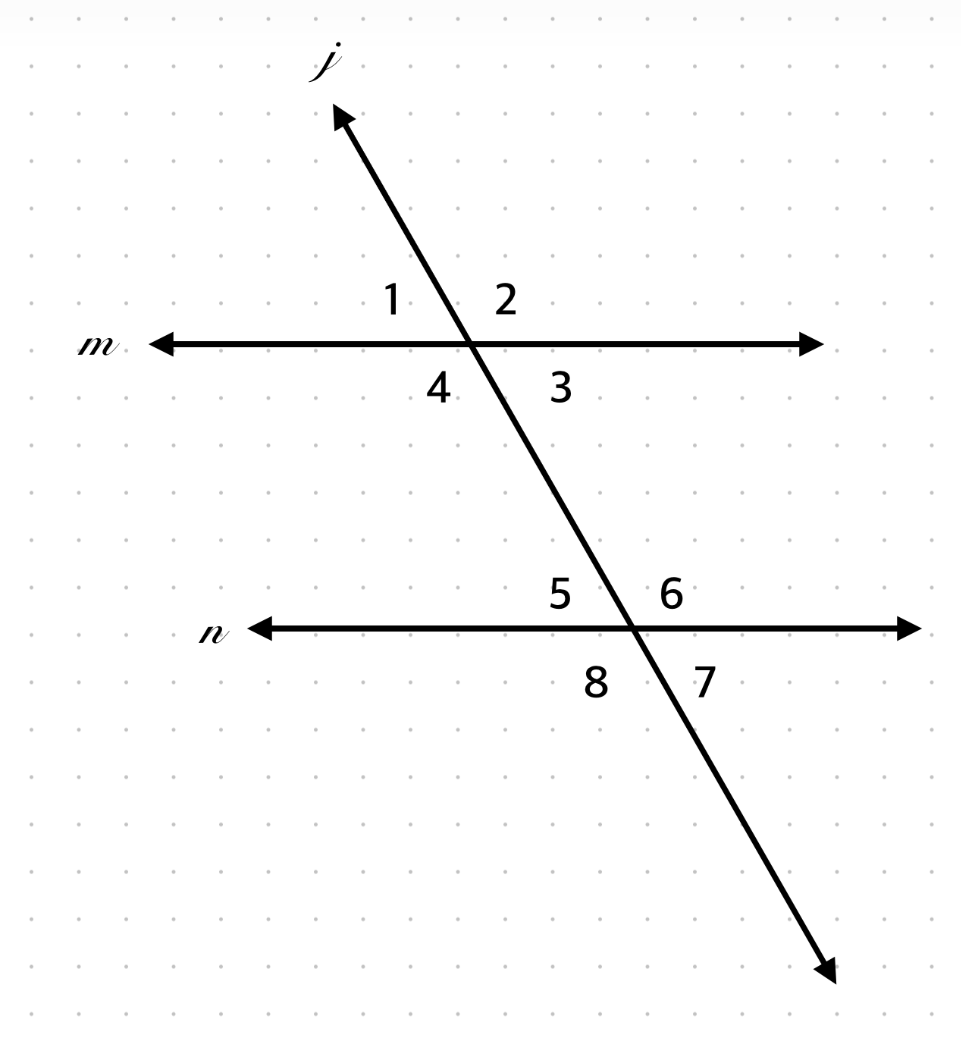
Linear pair → supplementary
400
If ∠1 = (3x – 40)° and ∠7 = (2x + 10)°, find x.
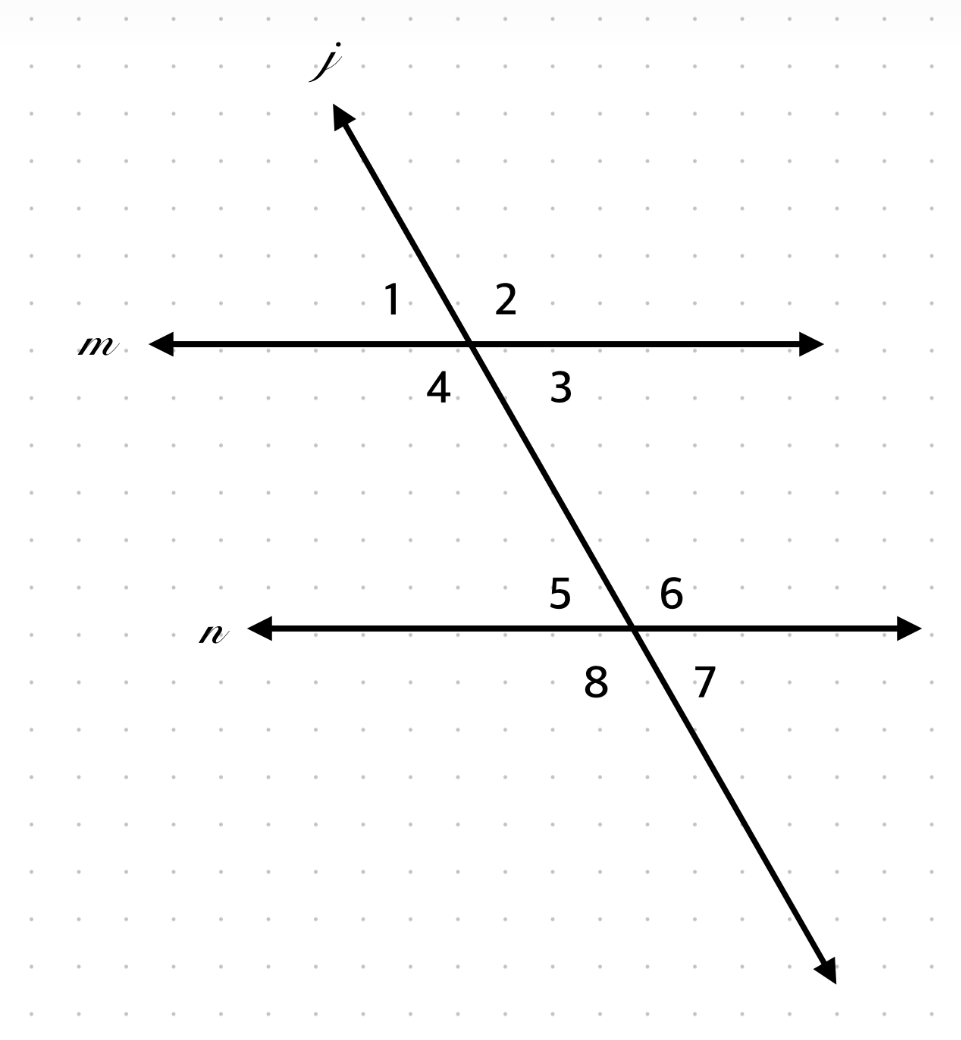
Alternate exterior → equal → 3x – 40 = 2x + 10 → x = 50
400
∠2 and ∠3?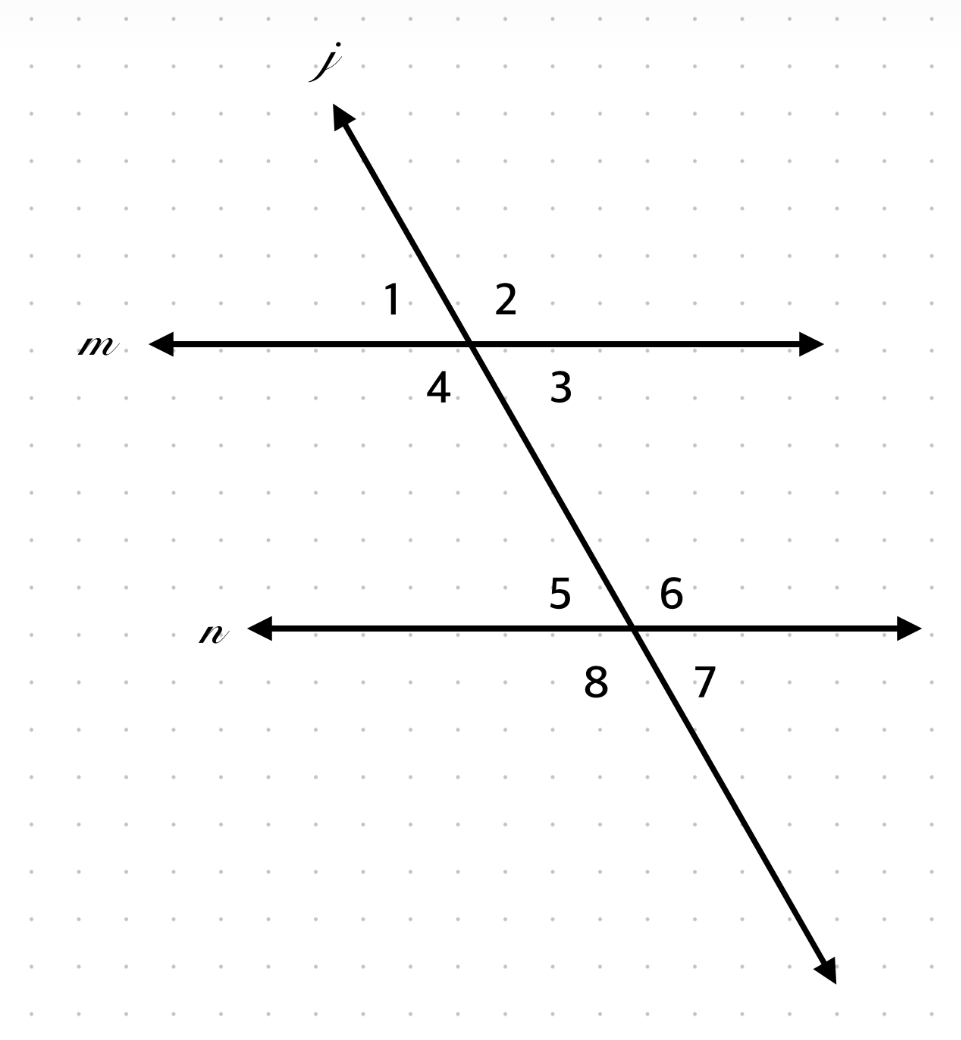
Supplementary, linear pair
400
If ∠7 = 65°, what is ∠2?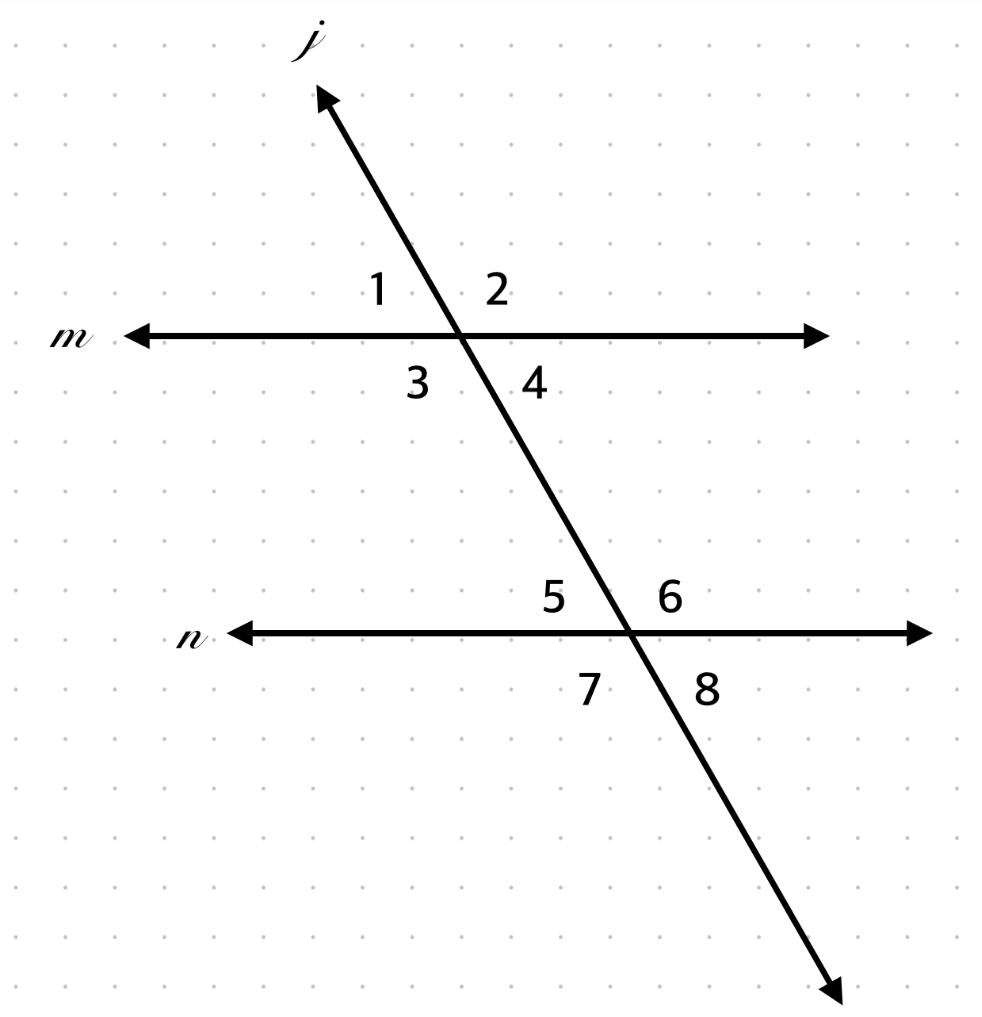
65°, alternate exterior
400
Explain why corresponding angles are congruent if the lines are parallel.
Parallel lines → equal slopes → transversal cuts at equal angles
500
∠4 and ∠6 are what type of angles?
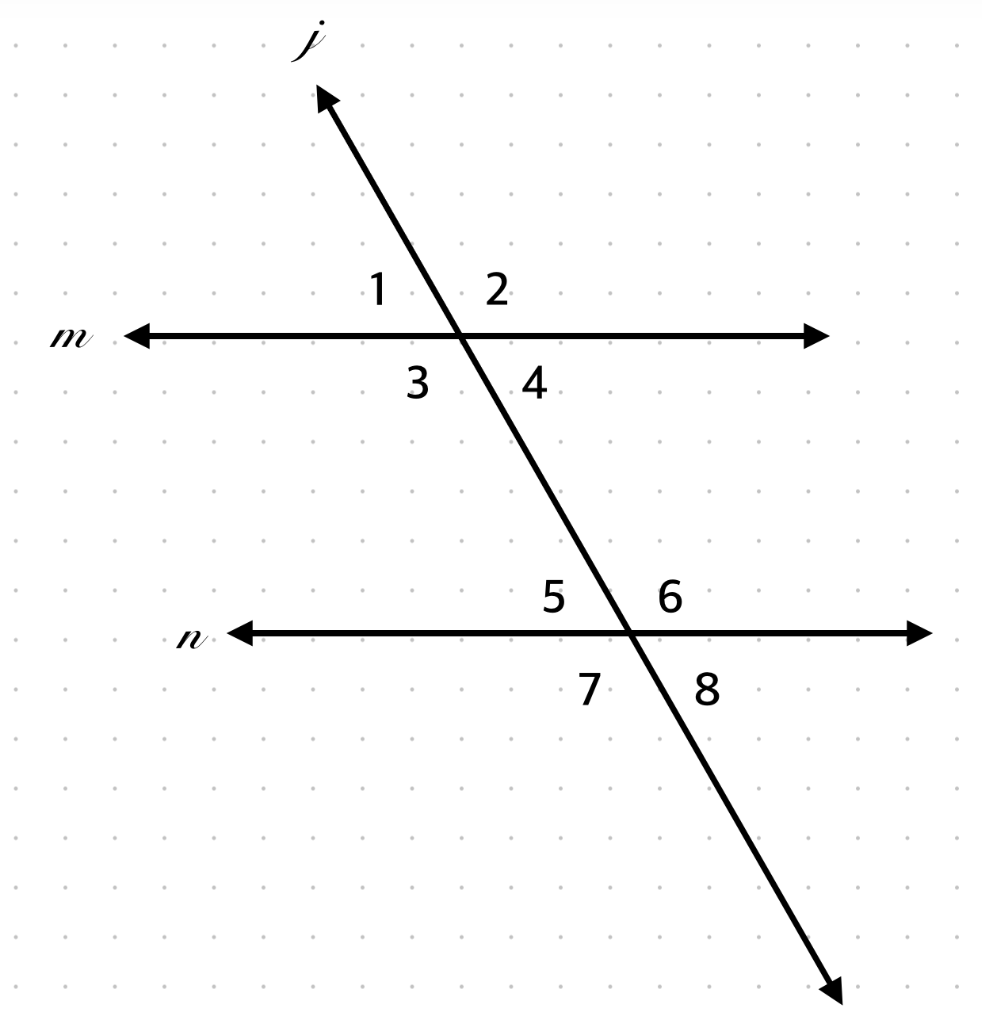
Same-side interior angles
500
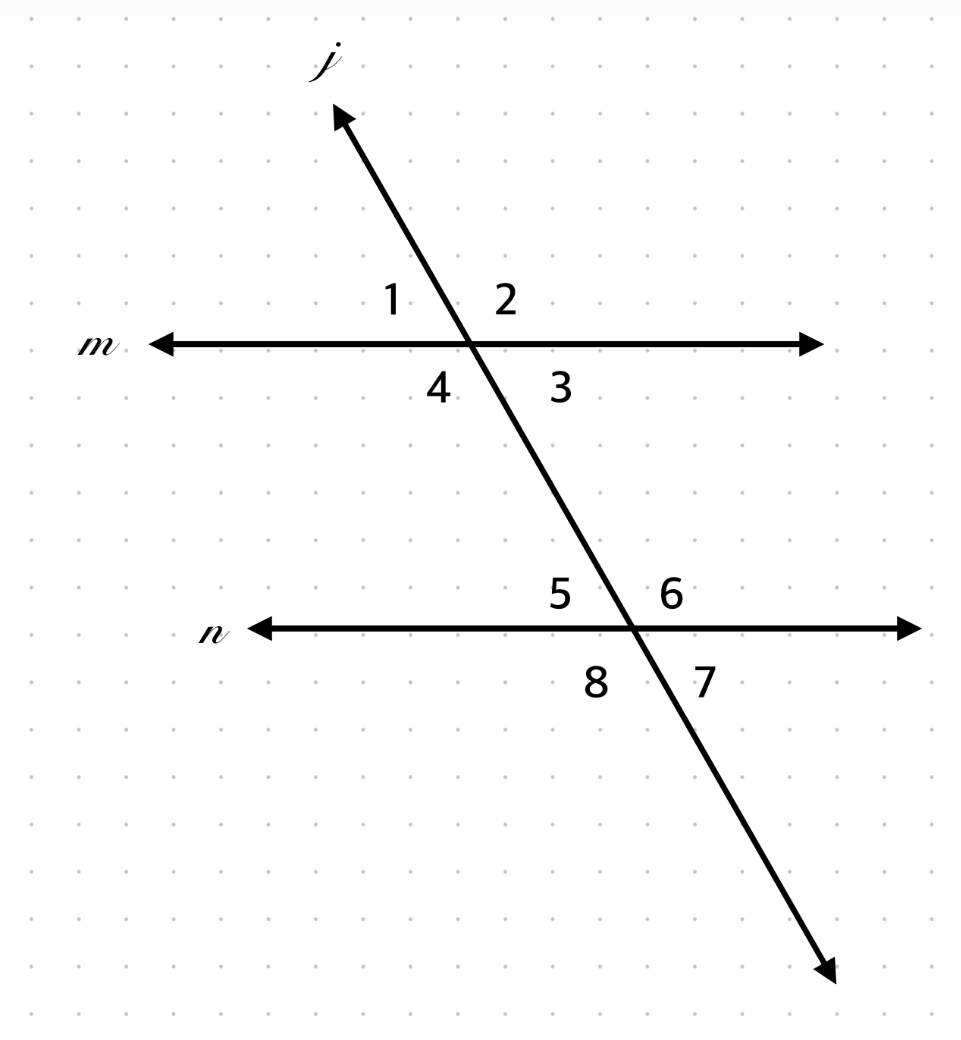If ∠5 = (4x + 25)° and ∠4 = (6x – 35)°, find x.
Same-side interior → sum 180 → 4x + 25 + 6x – 35 = 180 → x = 19
500
∠1 and ∠5?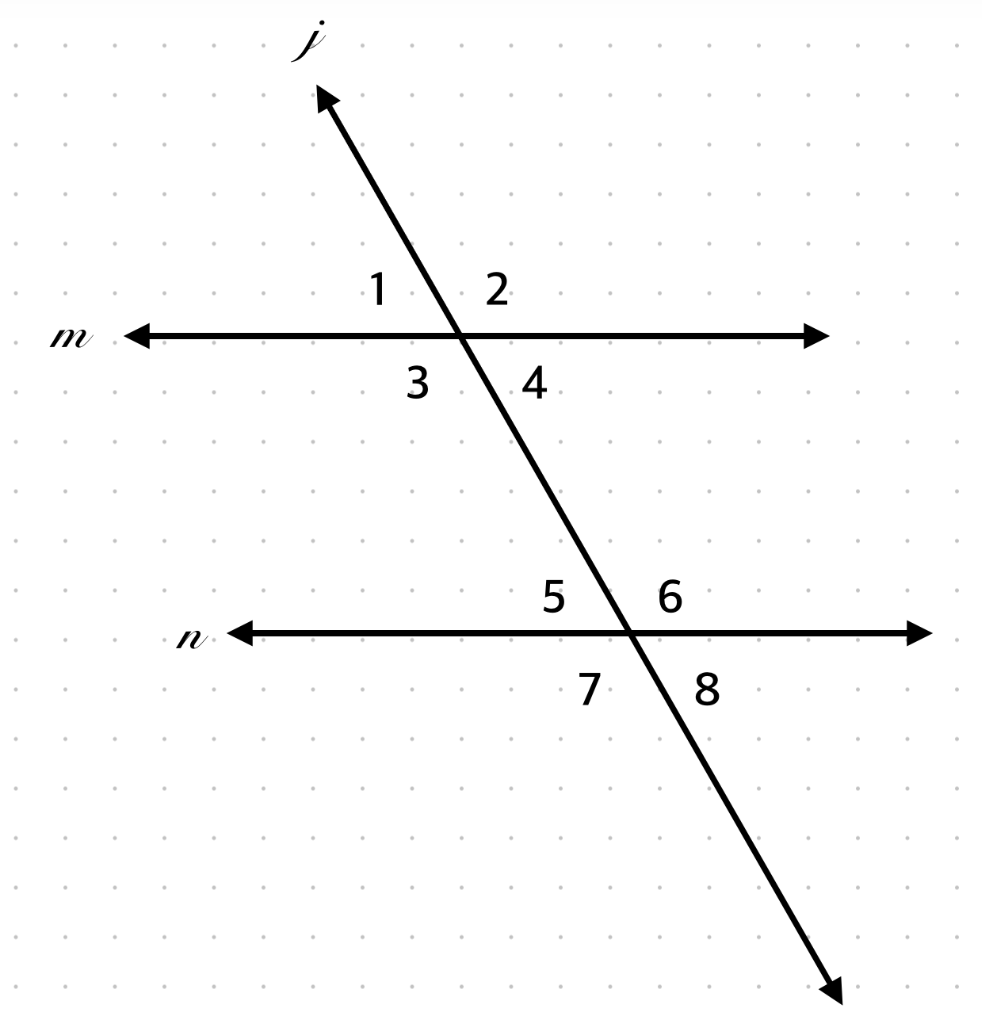
Congruent, corresponding
500
If ∠6 = 95°, what is ∠4?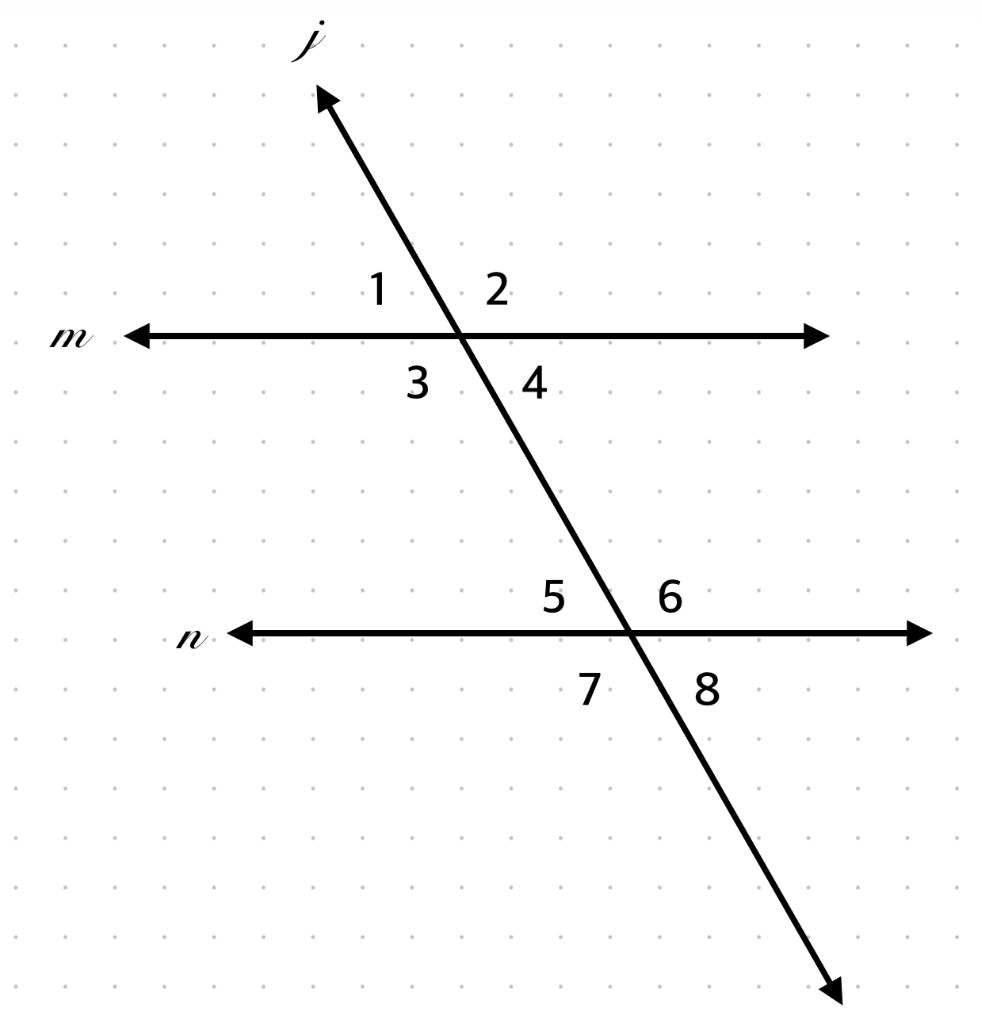
85°, same-side interior, supplementary
500
If lines are not parallel, are alternate interior angles always congruent?
No, only when lines are parallel.