Angles
Angle Pair Relationships
Find the missing angle measurement
Parallel Lines Cut by a Transversal
Angles of Triangles
Angles of Polygons
Similar Triangles
100
The point where the two sides (rays) start in an angle.
The vertex
100
Two angles whose measures add up to 90 degrees.
Complementary angles
100
Write an equation using b to show the angle relationship. Then find the missing angle measure (b).
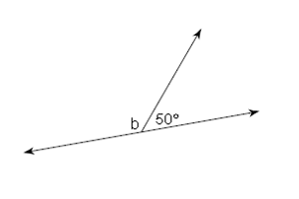
b + 50 = 180
130 degrees
100
Fill in the blank:
______________ angles are angles that are in the same position relative to the transversal and parallel line that it intersects. When two parallel lines are cut by a transversal, these angles are _________.
Corresponding
Congruent
100
Fill in the blank:
The sum of the measures of the three interior angles of a triangle is __________.
180 degrees
100
What formula can be used to find the interior angle sum of any polygon?
S =(n - 2)(180)
100
What do you need to know to prove that two triangles are similar?
You need to know that two angles of one triangle are congruent to two angles of another triangle (that there are 2 pairs of congruent angles).
200
An angle that measures greater than 0 degrees and less than 90 degrees.
Acute angle
200
Two angles whose measures add up to 180 degrees.
Supplementary angles
200
Write an equation using b to show the angle relationship. What is the missing angle measure (b)?
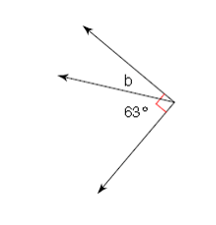
b + 63 = 90
27 degrees
200
Fill in the blank:
When two parallel lines are cut by a transversal, alternate interior angles and alternate exterior angles are __________.
Congruent
200
Complete the statement:
The measure of an exterior angle of a triangle is equal to the _____________________________________.
Sum of the measures of the two non-adjacent interior angles
200
Find the interior angle sum of a 13-gon.
1980 degrees
200
The triangles are similar. Find the value of x and justify your answer.
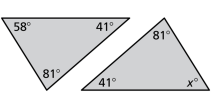
x = 58
In similar triangles, the three interior angle measures of one triangle will be the same as the three interior angle measures of the other triangle.
300
An angle that measures greater than 90 degrees and less than 180 degrees.
Obtuse angle
300
Two angles that are "next to" each other. They share a common vertex AND a common side.
Adjacent angles
300
Write an equation using x to show the angle relationship. Find the value of x.
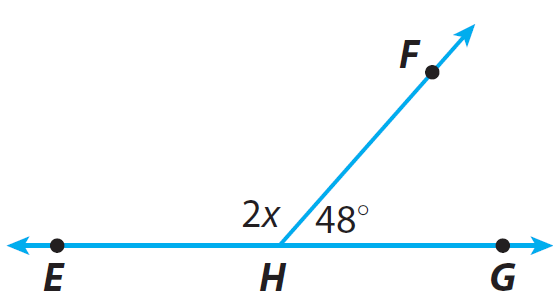
2x + 48 = 180
x = 66
300
Two parallel lines are cut by a transversal. If the measure of angle 2 is 40 degrees, what other angles also measure 40 degrees?
Angles 3, 6, and 7
300
A triangle has two interior angles measuring 30 degrees and 70 degrees. What is the measure of the third interior angle? Write an equation using x to represent the situation. Then find the missing angle measure.
30 + 70 + x = 180
80 degrees
300
Find the interior angle sum of a 19-gon.
3060 degrees
300
Are the triangles similar? Justify your answer and provide math evidence.
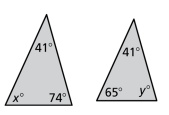
x + 74 + 41 = 180
x = 65
The triangles are similar because there are two pairs of congruent angles (the 41 degree angles and the 65 degree angles).
400
An angle that measures 90 degrees.
Right angle
400
Two non-adjacent angles, formed by intersecting lines, that are "across from" each other. They share a common vertex and their rays go in opposite directions.
Vertical angles
400
The measure of angle 3 is 35 degrees. What is the measure of angle 4? How do you know?
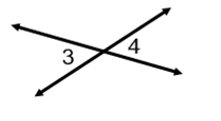
The measure of angle 4 is 35 degrees because angle 3 and 4 are vertical angles and vertical angles are congruent.
400
Two parallel lines are cut by a transversal. If the measure of angle 4 is 130 degrees, what do the other seven angles measure?
Angles 1, 5, and 8 measure 130 degrees.
Angles 2, 3, 6, and 7 measure 50 degrees.
400
Write an equation using z that represents the relationship between the angles in the diagram. Then find the value of z.
(z + 30) = (z - 81) + z
z = 111
400
Write an equation, using x, to represent the angle relationship in the diagram. Then find the value of x.
x + 159 + 84 + 167 + 104 + 126 + 140 = 900
x = 120
400
Are triangles ABC and DEC similar? Justify your answer and provide math evidence.
The triangles are similar. To prove this, find two congruent angle pairs. Use two angle pairs from below.
Angle pair #1: Angles ACB and DCE are vertical angles and are congruent.
Angle pair #2: Angles B and E are alternate interior angles and are congruent.
Angle pair #3: Angles A and D are alternate interior angles and are congruent.
500
An angle that measures 180 degrees.
Straight angle
500
Fill in the blanks:
Vertical angles are ____________________. They have the ______________ measure.
Congruent
Same
500
Write an equation using x to show the angle relationship. Find the value of x.
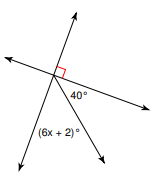
(6x + 2) + 40 + 90 = 180
OR
(6x + 2) + 40 = 90
x = 8
500
Two parallel lines are cut by a transversal. What is the relationship between angles 5 and 2? Justify your answer.
They are supplementary.
Justification: Angles 5 and 1 are corresponding angles and are congruent. Angles 1 and 2 are adjacent angles that form a straight angle, so they are supplementary. Therefore, since angles 5 and 1 have the same measure, angles 5 and 2 must be supplementary.
* Note: There are multiple justifications that will work.
500
Write an equation using x that represents the relationship between the angles in the diagram. Use your equation to find the missing angle measures.
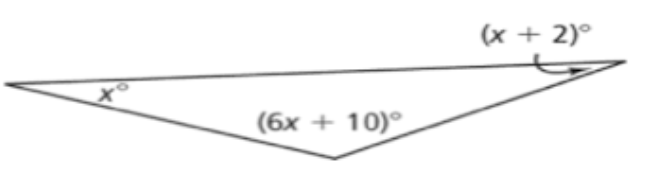
x + (x + 2) + (6x + 10) = 180
21 degrees, 23 degrees, and 136 degrees
500
Challenge: The polygon below is a regular polygon. This means that all sides have the same length. Write an equation, using x, to represent the angle relationship in the diagram. Then find the measure of each interior angle of the polygon.
8x = 1080
Each interior angle measures 135 degrees.
500
Are triangles ABC and DEC similar? Justify your answer and provide math evidence.
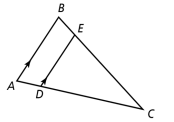
The triangles are similar. To prove this, find two congruent angle pairs. Use two angle pairs from below.
Angle pair #1: Angles ACB and DCE are a shared angle. Therefore, they are congruent.
Angle pair #2: Angles BAC and EDC are corresponding angles and are congruent.
Angle pair #3: Angles ABC and DEC are corresponding angles and are congruent.