Properties of Integration
Riemann Sums
Interpret that Integral
Summation Notation
Power Rule
100
int_2^9 5f(x) \ dx
35
100
If you are creating 6 rectangles that span an interval from [2,4], what is the width of each rectangle?
1/3
100
If the derivative determines instantaneous rate of change, the integral determines the...
area under the curve
or
accumulation of change
100
Determine the summation notation of the following integral:
int_0^2 x \ dx
lim_(n->oo)sum_(i=1)^n (2i)/n (2/n)
100
Solve the following definite integral using the power rule:
int_1^3 4 \ dx
8
200
int_9^7 3g(x) \ dx
-9
200
Find the exact area under the function.
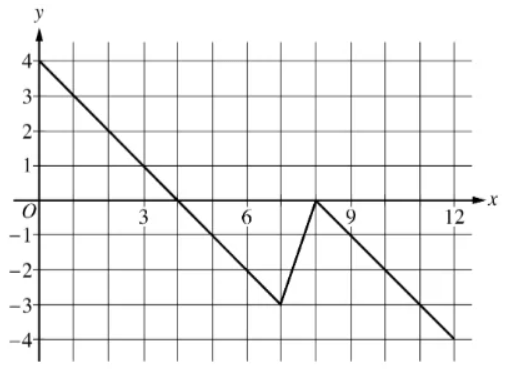
-6
200
Determine the integral that represents the following scenario:
The function s(t) represents the rate of change in the number of students in the VSA gym on Friday (t=time in hours). From 6 to 11am, the total change in students is 32 students. Let t = 0 be midnight.
int_6^11 s(t) \ dt = 32
200
Determine the summation notation of the following integral:
int_0^8 2x^2+6x \ dx
lim_(n->oo)sum_(i=1)^n ( 2(((8i)/n)^2) +6 ((8i)/n)) (8/n)
200
Solve the following indefinite integral using the power rule:
int \ 7x^6 \ dx
x7 + C
300
int_0^9 f(x) \ dx
11
300
x: | 2 | 4 | 6 | 8 | 10 |
f(x):| 3 | 7 | 10 | 13 | 15 |
Use LRAM to estimate the area with 4 subintervals for f(x) on the interval [2,10]
66
300
!!!!!!!!DAILY DOUBLE!!!!!!!!!!
Write a creative scenario for the following integral:
int_0^4 r(t) \ dt = 100
Anything including the independent being from 0 to 4 units, with a total accumulation of change in r(t) of 100
300
Determine the summation notation of the following integral:
int_3^9 3/(x^3) +8x \ dx
lim_(n->oo)sum_(i=1)^n ((3/((3+(6i)/n)^3)+(8(3+(6i)/n))(6/n)
300
Solve the following definite integral using the power rule:
int_8^10 6x^2-12x+8 \ dx
776
400
int_2^7 g(x) \ dx
-11
400
Find the exact area under the curve for the function.
-15/2+2\pi
400
The change in temperature of water in degrees F is modeled by k(t), where t is time in minutes. Interpret the integral in context.
int_3^6 k(t) \ dt = -4
From 3 minutes to 6 minutes, the temperature of the water decreased by 4 degrees F.
400
Determine the summation notation of the following integral:
int_2^4 3x^2 + 10x +5 \ dx
lim_(n->oo)sum_(i=1)^n (3((2+(2i/n))^2)+(10(2+(2i)/n))+5)(2/n)
400
Solve the following definite integral using the power rule:
int_1^4 sqrtx - 2x \ dx
-10.33
500
int_9^2 [4g(x)-f(x)] \ dx
39
500
Approximate the area under the curve over the interval [-3,2] using RRAM. Let n = 5.
f(x)=x^2+2x+2
20
500
The population of a town grows at a rate of r(t) people per year (where t = time in years). At time t = 2, the town's population is 1200 people. Write an integral that represents the town's population at t = 7.
1200 + int_2^7 r(t) \ dt
500
Determine the summation notation of the following integral:
int_5^12 sqrtx +3x^2 -5 \ dx
lim_(n->oo) sum_(i=1)^n (sqrt(5+(7i)/n) + (3((5+(7i)/n)^2))-5)(7/n)
500
Solve the following definite integral using the power rule:
int_4^12 3/(x^2) - 12x^3 + x/9 \ dx
-61432.388