Particle Motion
Related Rates
Linear Approximation
L'Hopital's Rule
Flores Math
100
How are position, velocity, and acceleration all related?
What is, they are all derivatives of each other? Velocity is the derivative of position and acceleration is the derivative of velocity?
100
Is there any difference between Related Rates and Implicit Differentiation?
What is, no! They're the same thing, but now we are working with actual word problems!
100
What is the equation of the tangent line?
What is,
y-y_1=m(x-x_1)?
100
When can you use L'Hospital's Rule
What is, when the limit is an indeterminate form?
100
Girl Math: If you purchase something with cash, what was the real price?
What is, free?
200
If v(t)>0 and a(t)>0 for a given time interval, then what is the particle doing?
What is, speeding up?
200
Common Error: What is a common thing most students forget to include on FRQs involving related rate problems?
What is, units?
200
Double Points: In essence, what is linear approximation?
What is, using the equation of the tangent line of a given point to estimate other points?
200
Double Points: What has Mr. Flores told you indeterminate forms are?
What is, a mystery? Something that can still be evaluated with some work? Indeterminate forms does not imply the limit does not exist!
200
Girl Math: If you paid half the amount using a gift card, then what was the real price?
What is, free?
300
How are speed and velocity related?
What is,
Speed=|v(t)|?
300
If
A=\pir^2
what is
\frac{dA}{dt}?
What is,
\frac{dA}{dt}=2\pir\frac{dr}{dt}?
300
Let f be a differentiable function such that f(1)=2 and f′(1)=9. What is the approximation for f(0.95) found by using the line tangent to the graph of f at x=1?
What is, y=1.55? Or f(0.95)=1.55?
300
Solve:
\lim_{x\to\infty}\frac{-3x^2+5x+1}{2x+1}
What is,
-\infty
?
300
Girl Math: If you ended up returning something, what did you really end up doing?
What is, gaining money?
400
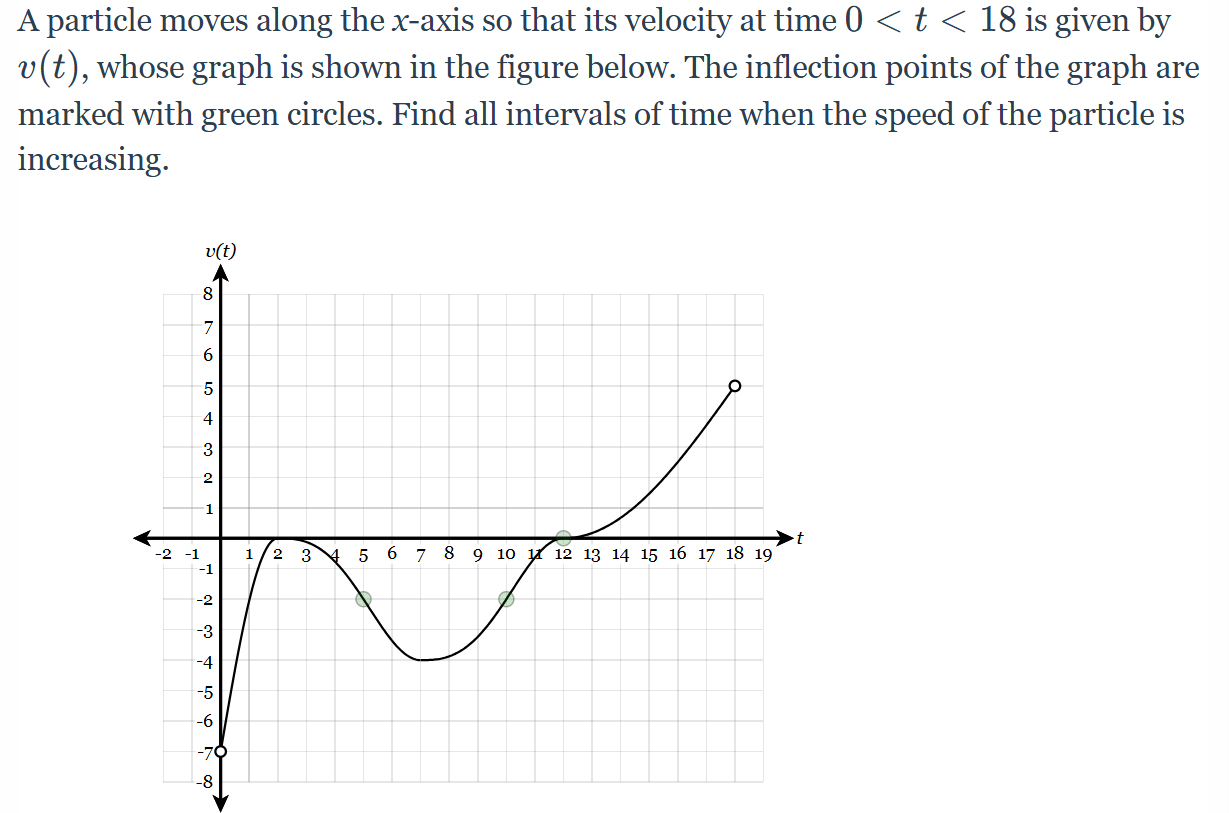
What is, (2,7) or (12,18)?
400
If
V=\pir^2h
what is
\frac{dV}{dt}?
What is,
\frac{dV}{dt}=\pi(2rh\frac{dr}{dt}+r^2\frac{dh}{dt})?
400
Let f be a differentiable function such that f(4)=−7 and f′(x)=−4x+10. What is the approximation for f(4.05) found by using the line tangent to the graph of f at x=4?
What is, y=-7.3? Or f(4.05)=-7.3?
400
Solve:
\lim_{x\to1}\frac{ln(2x-1)-1}{2-2x}
What is, DNE? Does Not Exist?
400
Flores Math: 45+45?
What is, 135? Shout out to all my gym rats.
500
A particle moves along the x-axis so that at time t≥0 its position is given by x(t)=−t^2−2t+35. Determine if the particle is moving to the right or to the left at t=6.
What is, left, since v(6)=-14?
500
Double Points: A right triangle has legs of 21 inches and 28 inches whose sides are changing. The short leg is decreasing by 3 in/sec and the long leg is shrinking at 3 in/sec. What is the rate of change of the area?
What is, \frac{dA}{dt}=-73.5 \text{in}^2/{sec}?
500
If the equation of a tangent line gives us a over estimate at a certain point, what does it tell us about the graph around that point?
What is, the graph is concave down?
500
Solve and give your answer in simplified form:
\lim_{x\to3}\frac{4\cos(3x-9)+2x}{5x^2+5}
What is,
\frac{1}{5}?
500
Flores Math: If Flores tells his fiance that a little project on his car is only going to take a couple of hours, how long is it really going to take?
What is, the entire weekend?