1.1-1.6 Review Polynomials
1.7-1.11 Review Rational Functions
1.12-1.14 Review
Ms Gangi MISC
100
Let f(x) be the function below. What is the degree of this function?
f(x)= x^2(x^2+4)(x-3)^3(x-1)
Degree 8
100
Determine if the following rational functions have a horizontal asymptote, slant asymptote or neither:
g(x)=(x^2+x-5)/(3x^2-2x+1)
Same degree so horizontal asymptote
100
Let r be a function that is a transformation of the function p such that
r(x)=5p(x/2)+3
Describe the transformations of the function p that result with the function r.
The function p is horizontally dilated by a factor of 2 and dilated vertically by a factor of 5 then translated vertically up 3 units.
100
Who is Ms. Gangi's favorite singer?
Taylor Swift
200
The graph of h is shown. Which of the following statements about h is correct?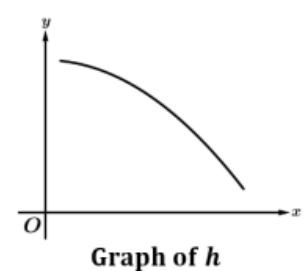
A) Rate of change is positive and decreasing
B) Rate of change is negative and decreasing
C) Function is negative and decreasing
D) Function is negative and R.O.C is negative
B) function is decreasing and concave down
200
Identify any hole or vertical asymptote:
g(x)=((x-3)(x+2))/((x-3)^2(x-8)
No hole because factor canceled out of the denominator but not in numerator. Vertical asymptote at x=3 and x=8
200
Let f(x) be equation below. Find g(-1)
g(x)=f(3x)+2
1
200
What is Ms. Gangi's favorite color?
yellow :)
300
Describe the end behavior of this function:
g(x)=4x^5-2x^4+3x-1
lim x-> -oo=-oo
lim x-> oo=oo
300
Write equation for slant asymptote:
h(x)=(4x^2-3x+5)/(x+2)
y=4x-11
300
The function k is constructed by applying three transformations to the graph of h in this order: a horizontal dilation by a factor of 2, a vertical dilation by a factor of 5, and a vertical translation by −9 units. If k(x) = ah(bx) + c, find the values of a, b, and c.
a = 5
b = 1/2
c = -9
300
What astrological sign is Ms. Gangi?
Sagittarius
400
Which could be the expression for this function: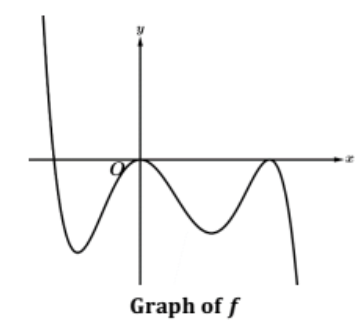
A) -x(x+2)(x-3)^2
B) -x(x+2)(x-3)
C) -x^2(x+2)(x-3)^2
D) x^2(x+2)(x-3)^2
C) odd degree w/negative leading coefficient
400
If a function has a vertical asymptote at x=-2 and a hole at x=3, write a rational function that could represent this function
f(x)=((x-3)(x-2))/((x-3)(x+2)
400
The domain of a function f is −10 ≤ x ≤ 0 and the range of f is −8 ≤ y ≤ 6. Find the domain and range of p, where p(x) = −3f(2x).
New Domain: −5 ≤ x ≤ 0
New Range: −18 ≤ y ≤ 24
400
Name one of the two other BPS high schools Ms. Gangi has worked at
Fenway High or English High
500
Factor this expression completely:
(x^2-9)(x^2-3x-18)
(x+3)^2(x-3)(x-6)
500
Identify the zero(s) of this function:
r(x)=(x^2+x-6)/(x^3-5x^2+6x)
x= -3
500
Fund quadratic regression model for this table:
y= 1.509x^2-15.138x+39.997
500
Ms. Gangi has now taught many pairs of siblings at BGA, name three pairs of them.
Edwin and Marcus, Nyeema and Josh, Sam and Josh, Naey and Anaylah, Kennedy and Cassidy, Anthony and Miguel, Eyoal and Able; Diego and Sevastian; Samarah, Leilani and Sabiene; Jose and Yari; Liya and Ali; Nani and Jenna Padilla; Vashawn and Navaeh Evans; and Ane, Ana and JJ Adorno.