Push it to the Limit
Graphic Content Warning
Factor-y Farming
Models and Makeovers
Calculator? I hardly know her
100
This function has up to two "turning points" and has end behavior that can be described by the following:
lim_(x->oo)f(x) = oo
lim_(x->-oo)f(x) = -oo
What is a function of odd degree?
100
Take some free points definitely had a good question and didn't run out of time yeah for sure.
Sick.
100
The following function has one of these when x=2.
f(x)=(x^2+8x+12)/(x^2-3x-10)
What is a hole?
100
This transformation is what can be seen in the following equation:
g(x)=f(1/3x)
What is a horizontal dilation (stretch) by a factor of 3?
100
If the following is true, then this is the average rate of change over the interval [-2,4].
f(-2)=9
f(4)=-3
What is -2?
-2
200
If the following is true, and f(3) is undefined, what occurs on the graph of f(x) at x=3?
lim_(x->3^-)f(x) = 4
lim_(x->3^+)f(x) = 4
What is a hole (3,4)?
200
What is the factor you'd find in the denominator of this rational function?
What is (x+1)?
200
If it has a factor that doesn't have any real zeroes, a polynomial must have an even number of these.
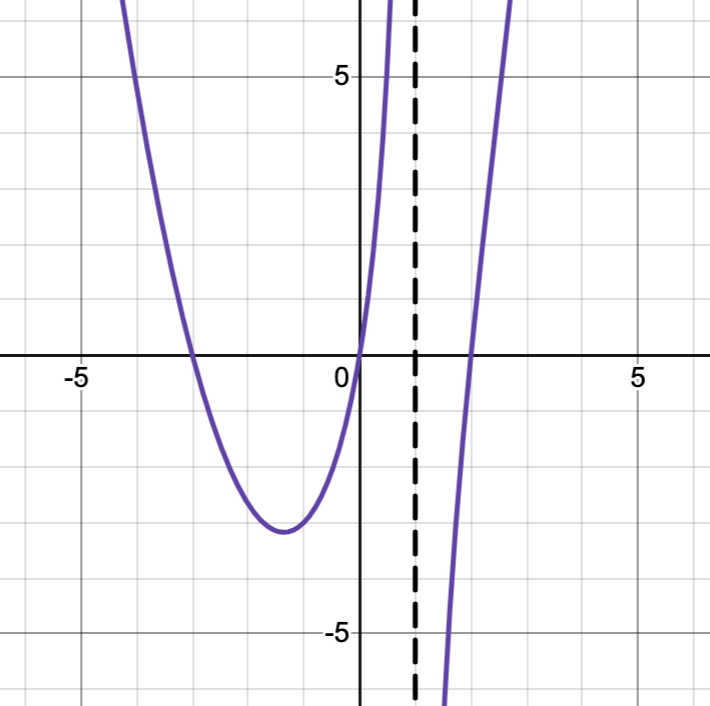
What is a non-real zero?
200
You'd run this type of regression on some data that looked roughly symmetrical.
What is a quadratic regression?
200
These are the decimal approximations (to the nearest hundreth) of the zeroes for the function
f(x)=-2.1x^{3}-1.9x^{2}+3.9x+1.2
What are x=-1.77, x=-.28, x=1.15?
300
If the following is true, and f(8) is undefined, what occurs on the graph of f(x) at x=8?
lim_(x->8^-)f(x) = +oo
lim_(x->8^+)f(x) = -oo
What is a vertical asymptote (at x=8)?
300
This word is used to describe the change in rate of change over the interval from A to B.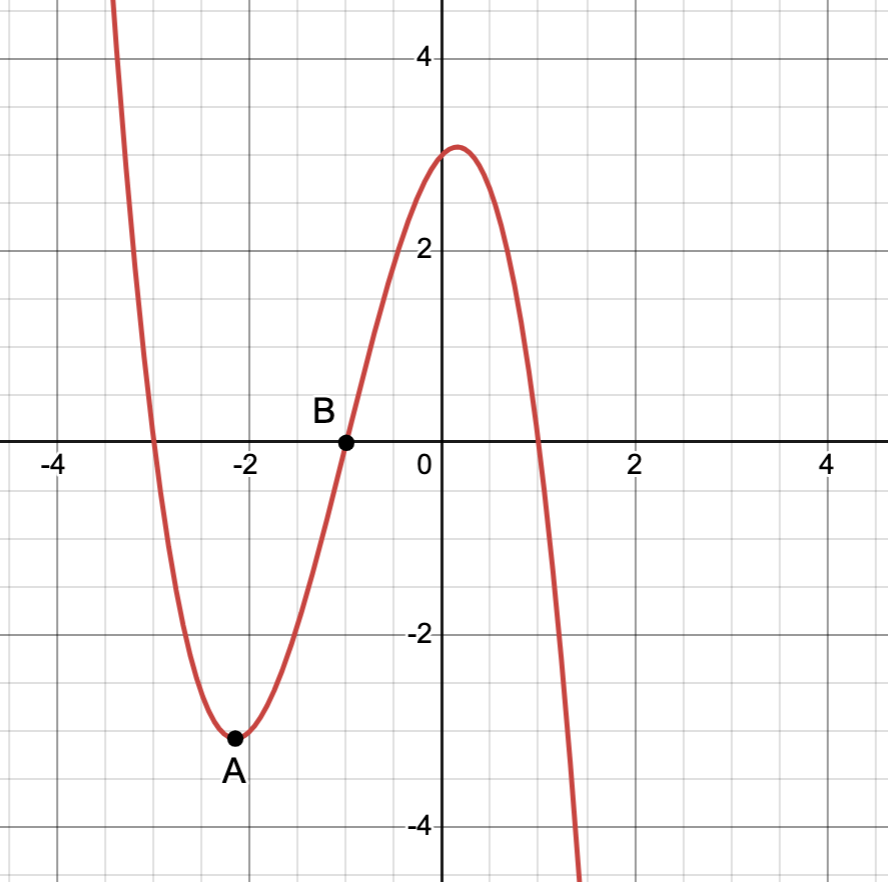
What is concave up?
300
This is the term used to describe how many times a particular factor appears in a polynomial function, causing the function to "bounce" off the x-axis if it's even.
What is multiplicity?
300
This table shows inputs and outputs from this type of function.
What is a cubic function?
300
This is the absolute maximum of the following function on the interval [-3,3]
f(x)=-x^3+x^2+4x-4
What is 20?
f(-3)=20
400
This would the the limit of the function as x increases without bound of
f(x)=(2x^3-9)/(3x^3-9x^2-6x)
What is 2/3? (horizontal asymptote at y=2/3)
Quotient of leading terms
400
This is how many inflexion points you see here.
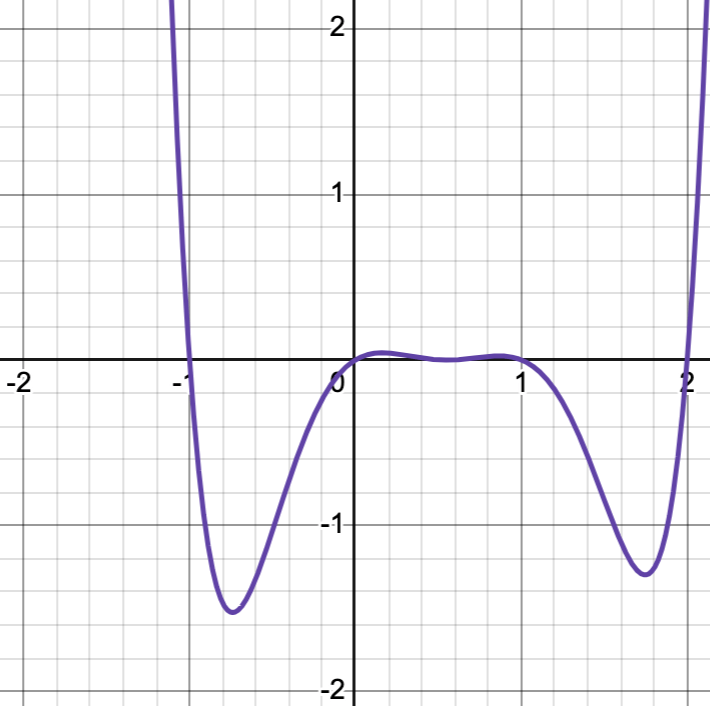
What is 4?
400
The function below has a domain of all real numbers, excluding these x-values.
f(x)=(x+8)/(x^3-3x^{2}-10x)
What are x=0, x=-2, x=5?
400
The volume of a cardboard box formed by folding up the sides of a 12in by 8in sheet of cardboard with corners of size x cut out if given by this cubic function in factored form.
What is V(x)=x(8-2x)(12-2x)
x is the height
8-2x is the width, 12-2x is the length, because of x by x corners cut out on both sides.
Volume is given by V(x)= length x width x height
400
Long division will show that f(x) has a slant asymptote at this linear function.
f(x) = (2x^2 + 5x + 4) / (x - 1)
What is y=2x+7?