Rational Functions
More Rational Functions
Model Fitting - must go in order
Transformations
Final Jeopardy - No Calculator
100
Find the domain of f(x)=\frac{2x+1}{x^2-3x-10} .
(-inf,-2)U(-2,5)U(5,inf) OR
x\ne 5 and x\ne -2
100
Determine which type of asymptote f(x)=\frac{4x^4-3x^3+4x+1}{5x^5-2x^2+1} would have: slant, horizontal, or neither.
Horizontal
100
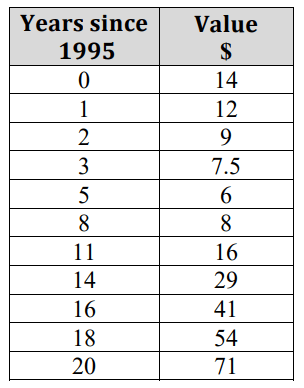The data above shows the value of a specific Beanie Baby over time. What type of model would be appropriate for this data?
quadratic
100
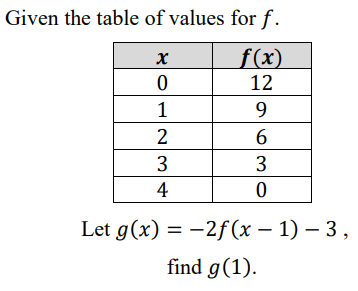
g(1)=-27
200
Find the zeroes of f(x)=\frac{2x+1}{x^2-3x-10}.
x=-1/2
200
F is inversely proportional to the square of 𝑟. If F=80 when r=5, find F when r=8.
F=31.25
200
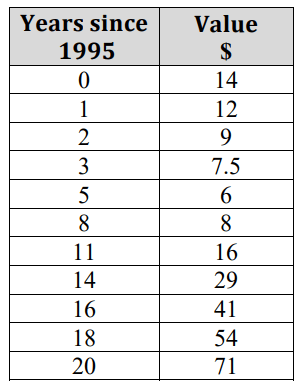
Write the equation of the regression curve.
f(x)=.298x^2-3.127x+14.246
200
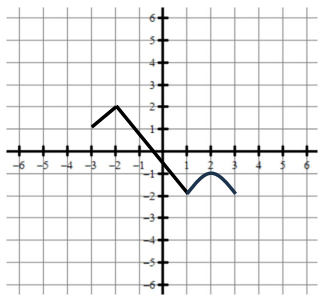
Use the graph of f to find g(x)=f(x-3)+4.
N/A
300
Find the y-intercept of f(x)=\frac{2x+1}{x^2-3x-10} .
y=-1/10
300
Find the 3rd term when (2x-3)^6 is expanded.
2160x^4
300
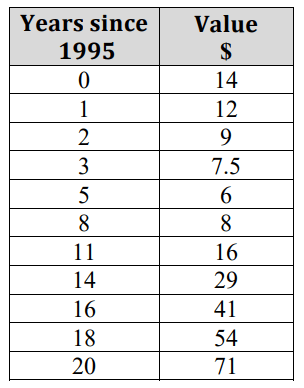Using the model, f(x)=.298x^2-3.127x+14.246 , predict the value of a Beanie Baby in 1999.
f(4)=$6.51
300
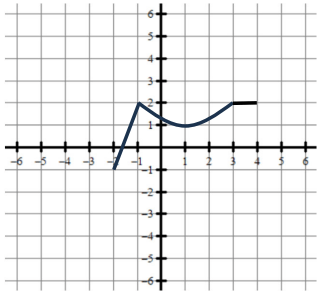
Use the graph of f to find g(x)=-f(2x)+5.
N/A
400
Determine the limit of f(x)=\frac{2x+1}{x^2-3x-10} as x->-∞ and as x->∞. Use proper notation.
0 and 0
400
Find the coordinates of the hole in f(x)=\frac{2x^2-10x}{x^2-2x-15} .
(5,1.25)
400
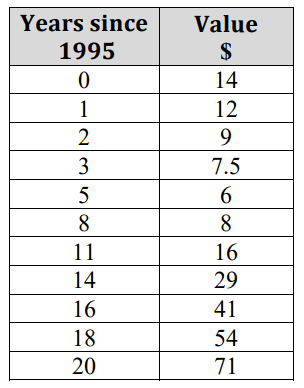Using our model, f(x)=.298x^2-3.127x+14.246 , find the average rate of change in Beanie Baby value from 2000 to 2010.
$2.83 per year
400
Let f(x)=x^2+3x-5 and g(x)=f(x+2) . Find g(x).
g(x)=x^2+7x+5
500
Determine the limit of f(x)=\frac{2x+1}{x^2-3x-10} as x-> -2^- and as x-> -2^+. Use proper notation.
left side: -∞ and right side: ∞
500
Find the equation of the slant asymptote of f(x)=\frac{4x^3-5x+3}{2x^2+3x} .
y=2x-3
500
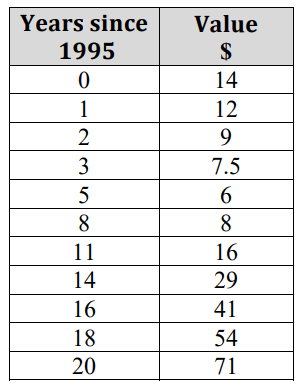
f(x)=.298x^2-3.127x+14.246
This will not be on the exam! Find the value of the residual at x=20. Remember: the residual is the difference between the predicted value and actual value. Order of subtraction: Actual-Predicted
Predicted: f(20)=70.906
Actual: 71
Actual-Predicted=71-70.906=.094
500
Let f(x)=3x+1 . Let
g(x)=-f(3x)+4 . Find g(x).
g(x)=-9x+3
500
Give me the x and y coordinates of the hole(s).
Domain: (-∞ ,0)U(0,2)U(2,∞)
Hole: (2,3)
Zero: x=-4
Vertical Asymptote: x=0