Sequences
Exponential Functions
Composition of Functions
Inverse Functions
Data Modeling
100
Find an explicit sequence that gives the nth term of the sequence. Assume a_0=15. {15,17,19,21,23,...}
a_n=15+2n
100
NO CALCULATOR Does the following function exhibit exponential growth or decay?
f(x)=6.7(5/21)^x
Exponential Decay
100
Find f(g(2)) when
f(x)=2^x AND\ g(x)=x^3-4x
1
100
Find
f^-1(0)
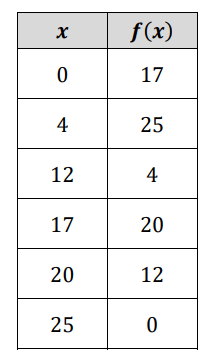
25
100
Identify the percent increase or decrease in the equation.
f(x)=10(.45)^x
55% decrease
200
Find a recursive sequence for the nth term of the sequence. {80,50,20,-10,...}
a_n=a_{n-1}-30
200
NO CALCULATOR Is the following function increasing or decreasing?
f(x)=-5(1/7)^x
Increasing
200
Express h as a composition of two simpler functions f and g.
h(x)=1/(x+6)
f(x)=1/x\ AND\ g(x)=x+6
200
Find g^-1(-1)
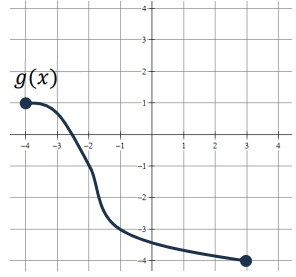
-2
200
Create a function to model the following scenario. A plague of mice has hit Australia! Starting with only 30 mice, their population 𝑝 increases by 650% every month, 𝑚.
p(m)=30(7.5)^m
300
Find an explicit sequence for the nth term of the sequence. Assume a_0=2/49.
\frac{2}{49},\frac{2}{7},2,14,...
a_n=\frac{2}{49}*7^n
300
Let f(x) be a function on which a transformation occurs. Let g(x) be a transformation of f(x). Name the transformation on f.
f(x)=81^x AND\ g(x)=9^x
horizontal dilation by factor of 2
300
Fill in the table when h(x)=f(g(x)) and f(x)=4^x.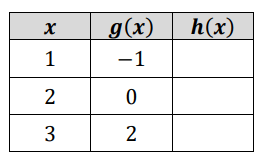
1/4, 1, 16
300
Find the inverse function of
f(x)=\frac {7}{x+4}
f^-1(x)=\frac{7}{x}-4
300
Create a function to model the following scenario. A mutual-fund portfolio has a value 𝑣 of $1,000 and doubles every 7 years 𝑡.
v(t)=1000(2)^(t/7)
400
Find the 42nd term in the sequence. {4,-6,-16,-26,...}
-406
400
Let f(x) be a function on which a transformation occurs. Let g(x) be a transformation of f(x). Name the transformation on f.
f(x)=2^x AND\ g(x)=-f(x)*8
shift left 3 units and reflection across the x-axis
400
Find f(g(x)) when
f(x)=\sqrt(3x+6)\ AND\ g(x)=x^2-1
f(g(x))=\sqrt(3x^2+3)
400
Find the domain and range of the inverse function
f^-1(x)
of f(x)=-\sqrt(x-6)-11
Domain:
x\le-11
Range:
y>=6
400
Create a function to model the following scenario. 700 grams of radioactive material 𝑚 decays at a rate of 2.4% per year 𝑡.
m(t)=700(.976)^t
500
Find the 12th term in the sequence. Give your answer as a fraction. {64, 16, 4, 1, 1/4,...}
1/65536
500
It is known that f(x) is an exponential function that passes through the points (1,10) and (6,2). Write an equation for f(x).
f(x)=2*(1/3)^(x-6) OR\ f(x)=10*((1/5)^(1/5))^(x-1)
500
Find the domain of g(f(x)) when
f(x)=\sqrt(6-x)\ AND\ g(x)=x+4
(-inf,6]
500
Find the domain and range of the inverse function f^-1(x)
of f(x)=(x+1)^2-7\ FOR\ x\le-1
Domain:
x\ge-7
Range:
y\ge-1
500
Use the table below to write an exponential function in the form f(x)=ab^x+k
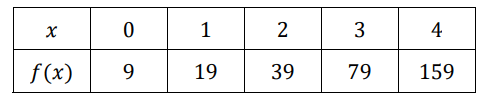
f(x)=10(2)^x-1