Inference Basics
Two Sample z Test/Interval
Two Sample t Test/Interval
Paired or Two Sample?
& Errors & p-value
& Errors & p-value
Mrs. Jordan Trivia
100
The general formula for margin of error.
critical value * standard error
100
What is the formula for the combined proportion (pc)?
pc= (x1+x2)/(n1+n2)
100
What degrees of freedom do you use in a two sample t test?
The smaller df out of the two samples.
100
A city planner is comparing traffic patterns at two different intersections. He randomly selects 12 times between 6 am and 10 pm, and he and his assistant count the number of cars passing through each intersection during the 10-minute interval that begins at that time. He plans to test the hypothesis that the mean difference in the number of cars passing through the two intersections during each of those 12 times intervals is 0. Which of the following is the appropriate test of the city planner’s hypothesis?
Paired t Test
100
How many siblings does Mrs. Jordan have?
2 brothers and 1 sister. 
200
The three conditions that must be checked before creating a confidence interval or performing a significance test.
random sampling
10% condition
large counts or large sample
200
Compute the test statistic for the given scenario:
H0: p1-p2=0
Ha: p1-p2>0
p1 = 0.5, n1 = 50
p2 = 0.45, n2 = 100
z = .579
200
This is the scenario when you pool for a two sample t test.
NEVER!
200
All of us nonsmokers can rejoice—the mosaic tobacco virus that affects and injures tobacco plants is spreading! Meanwhile, a tobacco company is investigating if a new treatment is effective in reducing the damage caused by the virus. Eleven plants were randomly chosen. On each plant, one leaf was randomly selected, and one half of the leaf (randomly chosen) was coated with the treatment, while the other half was left untouched (control). After two weeks, the amount of damage to each half of the leaf was assessed. For purposes of comparing the damage, which of the following is the appropriate type of procedure?
Paired t Test
200
How many nieces and nephews does Mrs. Jordan have?
3 nephews and 3 nieces
300
The reason we check the random condition
To generalize the results to the population.
300
If the confidence interval for the difference in proportions includes 0, what does that mean about the difference in proportions?
It is plausible that there is no difference in proportions.
300
Compute the p-value for the following:
Let n1=36, n2=41, x1=11.6, x2=10.4, s1=1.8 and s2=2.6.
Test the hypotheses--
H0 : µ1-µ2=0
Ha : µ1-µ2>0
p-value = 0.01
300
The following are percents of fat found in 5 samples of each of two brands of ice cream:
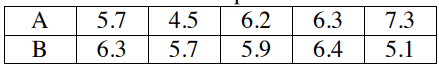
Which of the following procedures is appropriate to test the hypothesis of equal average fat content in the two types of ice cream?
Two Sample t Test
300
When did Mrs. Jordan graduate high school?
2007
400
The reason we check the 10% condition
To check for independence between observations in the sample.
Also need to check to use the standard deviation formula.
400
Popular wisdom is that eating presweetened cereal tends to increase the number of dental caries (cavities) in children. A sample of children was (with parental consent) entered into a study and followed for several years. Each child was classified as a sweetened-cereal lover or a unsweetened cereal lover. At the end of the study, the amount of tooth damage was measured. Here are the summary data:
Assuming the necessary conditions for inference are met, which of the following is an approximate 95% confidence interval for the difference in the mean tooth damage?
400
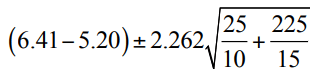
Compute a 90% confidence interval for the following:
Let n1=36, n2=41, x1=11.6, x2=10.4, s1=1.8 and s2=2.6
(0.36, 2.04)
df=71.3
400
In the 1990s a study was conducted in Seattle in which 518 cases were randomly assigned to treatments: 278 to CC plus standard MMR and 240 to CC alone. A total of 64 patients survived the heart attack: 29 in the group receiving CC plus standard MMR, and 35 in the group receiving CC alone. A test of significance was conducted on the following hypotheses.
H0: The survival rates for the two treatments are equal.
Ha: The treatment that uses CC alone produces a higher survival rate.
This test resulted in a p-value of 0.0761. Interpret the p-value.
Assuming the survival rates for the two treatments (CC alone and CC + MMR) are in fact the same, there is a 0.0761 probability of observing a difference between the two sample proportions (phatCC - phatcc+MMR) as large as or larger than the one observed, by chance.
400
When did Mrs. Jordan graduate college?
2011
500
The reason we check the large counts or large sample condition
To ensure that the sampling distribution of the sampling differences is approximately normal.
This allows use to calculate z and t or z* and t*.
500
Janice and her cousin Linda are a little competitive about the relative merits of their home towns. One contest they had was to determine who had more rainy days. They found weather records on the internet and each of them randomly selected 60 days from the past 5 years. Janice found that there had been measurable rainfall on 17 of the 60 days she selected for Asheville, and Linda found that there had been measurable rainfall on 12 of the 60 days she selected for Lincoln. They want to find if there is convincing evidence of no difference in the rainfall between their two cities.
Since the p-value=0.29>alpha=0.05 they fail to reject the null hypthesis and do not find convincing evidence that there is no difference in the rainfall between there two cities.
500
Daphnia pulicaria is a water flea—a small crustacean that lives in lakes and is a major food supply for many species of fish. When fish are present in the lake water, they release chemicals called kairomones that induce water fleas to grow long tail spines that make them more difficult for the fish to eat. One study of this phenomenon compared the relative length of tail spines in Daphnia pulicaria when kairomones were present to when they were not. Below are data on the relative tail spine lengths, measured as a percentage of the entire length of the water flea.
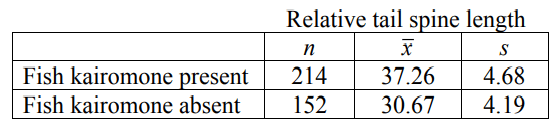
Do the data provide convincing evidence that the mean relative tail spine length of Daphnia is longer in the presence of fish kairomones? Assume the conditions for inference have been met.
Since the P-value is much less than any conventional value for α, we reject H0. We have strong evidence that the mean length of Daphnia pulicaria tail spines in the presence of fish kairomones is longer than when the kairomones are absent.
500
The Excellent Drug Company claims its aspirin tablets will relieve headaches faster than any other aspirin on the market. To determine whether Excellent’s claim is valid, 30 volunteers who are suffering from headaches are randomly assigned to two groups. The subjects in one group are given Excellent’s aspirin, and the subjects in the other group are given aspirin from the Simple Drug company. The number of minutes required for each subject to recover from the headache is recorded. A 5% significance level test is performed to determine whether Excellent’s aspirin cures headaches in significantly less time than Simple's aspirin and it is found that the p-valu e=0.3796.
What type of error could they have made in performing their significance test?
They could have made a type II error:
The company hasn’t concluded that Excellent aspirin works faster than Simple aspirin when it really does.
500
What is Mrs. Jordan's first name?
