6.2 El Dorado Community College has a main campus in the suburbs and a downtown campus. The amount X spent on tuition by a randomly selected student at the main campus has mean $732.50 and standard deviation $103. The amount Y spent on tuition by a randomly selected student at the downtown campus has mean $825 and standard deviation $126.50. Suppose we randomly select one full-time student from each of the two campuses. Calculate and interpret the mean of the sum S = X + Y
mean sum = 732.50 + 825 = $1,557.50;
the average of the sum of the tuitions would be about $1557.50 for many, many randomly selected pairs of students from each of the campuses.
7.1 Identify the population, the parameter, the sample, and the statistic in each setting.
How much do prices vary for filling a cavity? To find out, an insurance company randomly selects 10 dental practices in California and asks for the cash price for this procedure at each practice. The interquartile range is $74.
Population: All dental practices in California.
Parameter: The IQR of the price to fill a cavity for all dental practices in California.
Sample: The 10 randomly selected dental practices that provided the price they charge to fill a cavity.
Statistic: IQR = the interquartile range of the price to fill a cavity for the 10 selected dental practices = $74.
3.1 Identify the explanatory variable and the response variable for the following relationships, if possible. Explain your reasoning.
(a) The height and arm span of a sample of 50 teenagers 50
(b) The yield of corn in bushels per acre and the amount of rain in the growing season
(a) Either variable, height or arm span, could be the explanatory variable, because each could be used to predict or explain the other.
(b) Amount of rain is the explanatory variable
and yield of corn is the response variable.
Amount of rain may help predict or explain changes in the response variable, yield of corn. Yield of corn measures the outcome of the study.
DO Unit 6 100 First if not done!!!
6.2 Refer to Unit 6 100 problem: Note that X and Y are independent random variables because the two students are randomly selected from each of the campuses. Calculate and interpret the standard deviation of the sum S = X + Y.
Because X and Y are independent,
Std Dev = sqrt(103^2 + 126.5^2) = $163.13.
If many, many pairs of students are randomly and independently selected from each of the campuses, the sum of the tuitions will typically vary by about $163.13 from the mean of $1557.50.
7.2 Harley-Davidson motorcycles make up 14% of all the motorcycles registered in the United States. You plan to interview an SRS of 500 motorcycle owners. How likely is your sample to contain 20% or more who own Harleys?
mean = 0.14
StdDev = 0.0155
normalcdf (lower: 0.20, upper: 1000, mean: 0.14, SD: 0.0155) = 0.0001
2.3 Professional tennis player Novak Djokovic hits the ball extremely hard. His first-serve speeds can be modeled by a Normal distribution with mean 112 miles per hour (mph) and standard deviation 5 mph. Find the 85th percentile of Djokovic’s first-serve speeds.
invNorm(area: 0.85, mean: 112, SD: 5) = 117.18 mph.
6.1 Ana is a dedicated Skee Ball player who always rolls for the 50-point slot. The probability distribution of Ana’s score X on a randomly selected roll of the ball is shown here. μX = 23.8. Calculate and interpret the standard deviation of X.
Score: 10, 20, 30, 40, 50
Probability: 0.32, 0.27, 0.19, 0.15, 0.07
StdDev = 12.632; if many, many Skee Ball rolls are randomly selected, the point value will typically vary by about 12.632 from the mean of 23.8.
7.3 An insurance company claims that in the entire population of homeowners, the mean annual loss from fire is = $250 and the standard deviation of the loss is = $5000. The company hopes to sell 1000 of these policies for $300 each.
What is the probability that the mean loss from fire is greater than $300 for an SRS of 1000 homeowners?
If the company wants to be 90% certain that the mean loss from fire in an SRS of 1000 homeowners is less than the amount it charges for the policy, how much should the company charge?
1. normalcdf(lower: 300, upper: 1000, mean: 250, SD: 158.114) = 0.3759
2. invNorm(area: 0.90, mean: 250, SD: 158.114) = $452.63
4.2 An experiment that claimed to show that meditation lowers anxiety proceeded as follows. The experimenter interviewed the subjects and rated their level of anxiety. Then the subjects were randomly assigned to two groups. The experimenter taught one group how to meditate and they meditated daily for a month. The other group was simply told to relax more. At the end of the month, the experimenter interviewed all the subjects again and rated their anxiety level. The meditation group now had less anxiety. Psychologists said that the results were suspect because the ratings were not blind. Explain what this means and how lack of blindness could affect the reported results.
Because the experimenter knew which subjects had learned the meditation techniques, he or she is not blind. If the experimenter believed that meditation was beneficial, he or she may subconsciously rate subjects in the meditation group as being less anxious.
6.2 When a polling company calls a telephone number at random there is only a 9 percent chance that the call reaches a live person, and the survey is successfully completed. Suppose the random digit dialing machine makes 15 calls. Let X- the number of calls that result in a completed survey
Find the probability that more than 12 calls are not completed
Calculate and interpret Mean x
- Calculate and interpret StdDev Y
1. Let Y = number of calls not completed. Y has a binomial distribution with n = 15 and p = 0.91. binomcdf(15, 0.91, 12) = 0.8531. There is an 85.31% probability that more than 12 calls are not completed.
2. mean x = 15(0.09) = 1.35; if the machine made many sets of 15 calls, the average number completed would be about 1.35.
3. StdDev = sqrt(15(0.09)(0.91)) = 1.11; if the machine made many sets of 15 calls, the expected number of completed calls would typically vary from the mean (1.35) by about 1.11 calls
7.1 List all 6 possible SRSs of size n = 2, calculate the proportion of red cars in each sample, and display the sampling distribution of the sample proportion on a dotplot. Is the sample proportion an unbiased estimator of the population proportion? Explain your answer.

1.3 Consumer Reports magazine rated different types of refrigerators, including those with bottom freezers, those with top freezers, and those with side freezers. One of the variables they measured was annual energy cost (in dollars). The following boxplots show the energy cost distributions for each of these types. Compare the energy cost distributions for the three types of refrigerators.
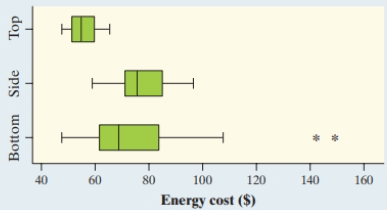
Shape: The distribution of energy cost (in dollars) for top freezers looks roughly symmetric. The side freezers look roughly symmetric. The bottom freezers look skewed to the right.
Outliers: There are no outliers for the top or side freezers. There are at least two bottom freezers with unusually high energy costs (over $140 per year).
Center: The typical energy cost for the side freezers (median=$75) is greater than the typical cost for the bottom freezers (median=$69), which is greater than the typical cost for the top freezers (median=$56).
Variability: There is much more variability in the energy costs for bottom freezers (IQR=$20), than for side freezers (IQR=$12), than for top freezers (IQR=$8).
6.3 To start her old lawn mower, Rita has to pull a cord and hope for some luck. On any particular pull, the mower has a 20% chance of starting.
a. Find the probability that it takes her exactly 3 pulls to start the mower.
b. Find the probability that it takes her 6 or more pulls to start the mower.
a. geometpdf(p: 0.20, x value: 3) = 0.128. There is a 0.128 probability that it takes Rita exactly 3 pulls to start the mower.
b. geometcdf(p: 0.20, x value: 6) + geometpdf(p: 0.20, x value: 6) = 0.2621 + 0.0655 = 0.3276. There is a 0.3276 probability that it takes 6 or more pulls to start the mower.
7.3 In response to the increasing weight of airline passengers, the Federal Aviation Administration (FAA) told airlines to assume that passengers average 190 pounds in the summer, including clothes and carry-on baggage. But passengers vary, and the FAA did not specify a standard deviation. A reasonable standard deviation is 35 pounds. A commuter plane carries 30 passengers. Find the prob-ability that the total weight of 30 randomly selected passengers exceeds 6000 pounds. (Hint: To calculate this probability, restate the problem in terms of the mean weight.)
mean = 190
StdDev = 6.3901
normalcdf(lower: 200, upper: 1000, mean: 190, SD: 6.3901) = 0.0588
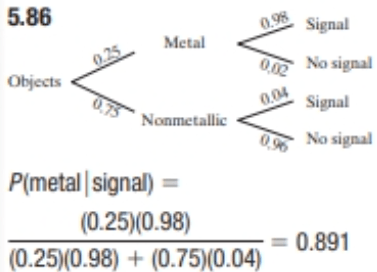
5.3 A boy uses a homemade metal detector to look for valuable metal objects. The machine isn’t perfect—it beeps for only 98% of the metal objects over which it passes, and it beeps for 4% of the nonmetallic objects over which it passes. Suppose that 25% of the objects that the machine passes over are metal. Choose an object from this beach at random. If the machine beeps when it passes over this object, find the probability that the boy has found a metal object. (Hint: Make a tree diagram to list possible probabilities)