Rewrite in terms of sin(x) and cos(x).
cos (x − 5π/6)
What is sin(x)/2 - 1/2 sqrt 3 cos(x) ?
Find all exact solutions on the interval 0 ≤ θ < 2π.
2 sin(θ) = − 2
2
What is θ =5pi/4, 7pi/4 ?
Given a vector with initial point (−8, 1) and terminal point (7, −7), find an equivalent vector whose initial point is (0, 0). Write the vector in component form 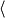 a, b
a, b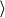 .
.
What is (15, -8) ?
Assume α is opposite side a, β is opposite side b, and γ is opposite side c. If possible, solve the triangle for the unknown side. Round to the nearest tenth. (If not possible, enter IMPOSSIBLE.)
β = 51.1°, a = 10.7, c = 13.9
b=?
What is b= 11.0 ?
Use the given vectors to compute u + v, u − v, and 5u − 3v.
u = 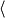 6, −3
6, −3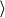 , v =
, v = 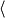 7, 2
7, 2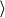
u + v =
u − v =
5u − 3v =
What is u + v = (13, -1), u − v = (-1, -5)
5u − 3v = (9, -21) ?
Simplify to an expression of the form (a sin(θ)).
2 sin(π/8) 2 cos(π/8)
What is 2sin(pi/4)?
Find all exact solutions on [0, 2π).
2 cos2(t) − 3 cos(t) = −1
What is t= pi/3, 5pi/3, 0 ?
Find the magnitude and direction of the vector, 0 ≤ θ < 2π.
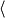 1, 4
1, 4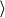
magnitude = ?
direction θ = ?
What is magnitude= sqrt 17, direction θ = tan-1(4) ?
Solve the triangle. Round to the nearest tenth.
a = 17, b = 14, c = 18
A= ?°
B= ?°
C= ?°
What is A= 62.7° B= 47.0° C= 70.2° ?
Convert the given polar coordinates to Cartesian coordinates.
(4, − π/4)
(x, y) = ( )
What is (2 sqrt 2, -2 sqrt 2) ?
Find the exact values of the half angles.
Find sin(θ/2), cos(θ/2), and tan(θ/2).
What is sin(θ/2)= sqrt 17/17, cos(θ/2)=4 sqrt 17/17, and tan(θ/2)= 1/4 ?
Find a possible formula for the trigonometric function represented by the given table of values.
y=?
X axis: 0, π/4, π/2, 3π/4, π, 5π/4, 3π/2
Y axis: −2, 2, 6, 2, −2, 2, 6
What is y= 2 - 4cos(2x) ?
Given initial point P1 = (1, 2) and terminal point P2 = (−9, 3), write the vector v in terms of i and j.
Draw the vector on the graph.
What is -10i + j and  ?
?
Two planes leave the same airport at the same time. One flies at 20° east of north at 400 miles per hour. The second flies at 30° east of south at 500 miles per hour. How far apart are the planes after 2 hours? (Round your answer to the nearest mile.)
mi =?
What is 1,634 mi ?
Graph the polar equation.
r = 8 sin(θ)
Identify the name of the shape.
What is  , and Leminscate ?
, and Leminscate ?
If sin(x) = − 12/13 and x is in quadrant III, find the exact values of the expressions without solving for x.
a) sin (x/2)
b) cos (x/2)
c) tan (x/2)
What is sin(x/2)=3 sqrt 13/ 13, cos(x/2)=-2 sqrt 13/ -13, and tan(x/2)=-3/-2 ?
A certain bay with very high tides displays the following behavior. In one 12-h period the water starts at mean sea level, rises to 14 ft above, drops to 14 ft below, then returns to mean sea level. Assuming that the motion of the tides is simple harmonic, find an equation that describes the height of the tide in this bay above mean sea level. (Let y be the height above sea level in feet, and t the number of hours since the start of the 12-h period.)
y=?
Sketch a graph that shows the level of the tides over a 12-h period.
What is y= 14sin(pi/6 t), and
 ?
?
Find the length of side x. Round to the nearest tenth.
x=?

What is x=11.1 ?
Solve for the unknown side. Round to the nearest tenth.

What is 21.7 ?
Use the vectors shown to sketch u − 3v.

What is  ?
?
Rewrite the sum as a product of two functions. Leave your answer in terms of sine and/or cosine.
cos(56°) + cos(28°)
Calculate this value numerically. (Round your answer to four decimal places.)
What is 2cos(14degrees) cos(42degrees), and 1.4421 ?
Each time your heart beats, your blood pressure increases, then decreases as the heart rests between beats. A certain person's blood pressure is modeled by the function p(t) = 110 + 25 sin(168πt)where p(t) is the pressure (in mmHg) at time t, measured in minutes.
(a) Find the amplitude, period, and frequency of p.
(b) Sketch a graph of p.
What is
A) amplitude=25, period=0.0119, frequency=84
B)
 ?
?
Assume α is opposite side a, β is opposite side b, and γ is opposite side c. Determine whether there is no triangle, one triangle, or two triangles. Then solve each triangle, if possible. Round each answer to the nearest tenth.
a = 2.4, c = 1.7, γ = 38°
α1 = °
α2 = °
β1 = °
β2 = °
b1 =
b2 =
What is α1 =60.4 ° α2 = 119.6° β1 = 81.6°
β2 =22.4 ° b1 = 2.7 b2 =1.1 ?
To determine how far a boat is from shore, two radar stations 300 feet apart find the angles out to the boat, as shown in the figure below. Determine the distance of the boat from station A and the distance of the boat from shore. Round your answers to the nearest whole foot.
distance from boat to station A ft=?
distance from boat to shore ft=?
Bottom left angle of the triangle is 65 degrees and bottom right angle is 60 degrees.
What is distance from boat to station A 317ft and
distance from boat to shore 287ft ?
Find all exact solutions on the interval [0, 2π).
cos(8x) + cos(4x) = 0
x=?
What is x= pi/12, 7pi/12, 13pi/12, 19pi/12, 5pi/12, 11pi/12, 17pi/12, 23pi/12, pi/4, 3pi/4, 5pi/4, 7pi/4 ?