Exponential equivalent for m=log_3 81 ?
3^m=81
g(x)=5^x What is g^-1(x) ?
\log_5 x
End behavior of 2\log x
\lim_(x->\infty)f(x)=\infty \lim_{x->0^+} f(x)=-\infty
Condense c\log_b a where a, b, c are positive integers
\log_b a^c
Change to base 3: \log_2 10
\frac{\log_3 10}{\log_3 2}
Exponential equivalent for \log_4 \frac{1}{64} = -3 ?
4^-3=\frac1{64}
What's the value of f^-1(32) ?
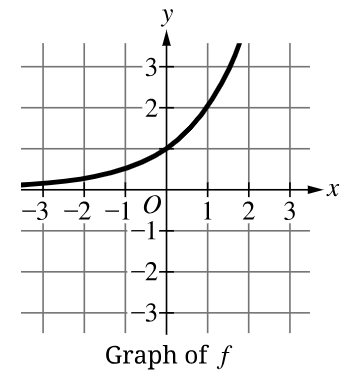
5
End behavior of -\log x
\lim_(x->\infty)f(x)=-\infty \lim_{x->0^+} f(x)=\infty
Describe transformation f(x)=\log x->g(x)=\log x^3
Vertical dilation by a factor of 3
Change to base 10: \log_2 10
\frac{1} {\log_10 2}
Logarithmic equivalent for 6^3=216 ?
\log_6 216 = 3
The function f is an increasing function such that every time the output values of the function f increase by 1, the corresponding input values multiply by 4. What is the definition of f(x)?
\log_4 x
Concavity of e^{2x}
Up
Describe transformation f(x)=\log x->g(x)=-\log (x-3)
Horizontal shift, right 3
Vertical reflection
Change to base 7: \log_49 10
\frac{\log_7 10}{2}