Logs/Exponents
Sequences/Series
Trig (Chpt 4)
Limits
Analytic Trig (Chpt 5)
100
Find x:
log_2(4)=x
x=2
100
Write the first 6 terms of the sequence:
a_n=2n
2, 4, 6, 8, 10, 12
100
Find an angle coterminal with
(21pi)/4
(5pi)/4, (13pi)/4, (29pi)/4, etc
100
When evaluating a limit and you get
0/0
what must do?
More work!
100
Simplify:
sec(x) - tan(x)sin(x)
cos(x)
200
Write in
log(1000)=3
exponential form
10^3=1000
200
Write a (non recursive) equation for the
n^(th)
term of the following sequence:
1, 7, 13, 19, 25,...
a_n=1+6(n-1)
a_n=6n-5
200
Convert to radians:
-36^@
-36^@*((pi rad)/180^@)=-pi/5
200
lim_(x->3)(x-4)
-3
200
Verify the following identity:
(Sin(x+y))/((cosx)(cosy)) = tanx + tany
(sinx*cosy+cosx*siny)/(cosx*siny)
(sinx*cosy)/(cosx*cosy)+(cosx*siny)/(cosx*cosy)
sinx/cosx+siny/cosy = tanx + tany
300
Write
log_7(49)=2
in exponential form
7^2=49
300
Write out the first 5 terms of the following sequence:
a_n=3*3^(n-1)
3, 9, 27, 81, 243
300
Find the 6 trig values at the point
(-8/17, 15/17)
sintheta=15/17,
costheta=-8/17,
tantheta=-15/8,
csctheta=17/15,
sectheta=-17/8,
cottheta=-8/15
300
lim_(w->0)(w/(1/(-1+w)+1))
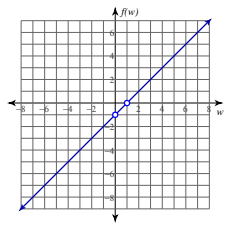
-1
300
Verify the following:
cos^2x+cos^2x*cot^2x=cot^2x
cos^2x(1+cot^2x)=
cos^2x*csc^2x=
cos^2x/sin^2x=cot^2x
400
Solve for x:
log_x625=4
x^4=625
x=root(4)625
x=5
400
Write an equation (non recursive) for the
n^(th)
term of the following sequence:
2, 1, 1/2, 1/4, 1/8, ...
a_n=2*(1/2)^(n-1)
400
Solve for
theta:
csctheta=(2sqrt(3))/3
0^@<theta<90^@
60^@
400
lim_(x->1)(x^2-7x+6)/(x^2-1)
Factor and cancel!
-5/2
400
Verify the following:
cos^2x/(1+sinx)=1-sinx
(1-sin^2x)/(1+sinx)=
((1+sinx)(1-sinx))/(1+sinx)=
1-sinx
500
Condense the following to be an expression with one log:
1/3[2ln(x+3)+ln(x)-ln(x^2-1)]
ln[((x+3)^2*x)/(x^2-1)]^(1/3)
500
Is the following sequences Arithmetic, Geometric, or neither?
1, 2, 6, 24, 120, ...
Neither!
(What sequence is it?!?)
500
Find the equation of this graph:
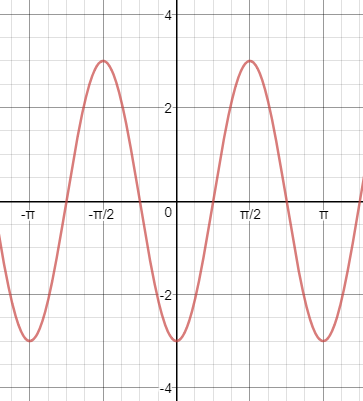
y=-3cos(2x+4pi)
500
lim_(x->oo)(5x^3-4x^2-5x)/(3x+4x^3)
5/4
500
Solve for x in the following:
1/2secx-1=0
x=pi/3,(5pi)/3