Vocabulary
Angles
Angles Part II
Midpoint & Distance Applications
Angle Applications
100
An object that has a starting point and goes infinitely in one direction.
What is a ray.
100
How many rays form the sides of an angle?
What is 2.
100
An angle that measures between 90 and 180 degrees.
What is an obtuse angle.
100
Write out the midpoint and distance formulas.
Midpoint: ((x_1+x_2)/2, (y_1+y_2)/2)
Distance: c=sqrt((x_2-x_1)^2+(y_2-y_1)^2
100
What angle relationship do <BOC and <COD have?
They are complementary.
200
A basic geometric object that has two endpoints.
What is a line segment.
200
The name of the point where an angle 'bends.'
What is the vertex.
200
An angle that measures between 0 and 90 degrees.
What is an acute angle.
200
Find the midpoint of the segment AB with endpoints A(-2, 6) and B(-10, 1).
((x_1+x_2)/2, (y_1+y_2)/2)
((-2+(-10))/2, (6+1)/2)
(-12/2, 7/2)
(-6, 3.5)
200
What angle is a linear pair with <EOD?
<AOE or <COD
300
A geometric object that goes infinitely in two directions.
What is a line.
300
The name given to opposite angles formed by the intersection of two lines.
What is vertical angles.
300
Two angles whose sum of measures is 180 degrees.
What are supplementary angles.
300
Find the length of the segment AB with endpoints A(-2, 6) and B(-10, 1).
c=sqrt((x_2-x_1)^2+(y_2-y_1)^2)
c=sqrt((-10+2)^2+(1-6)^2)
c=sqrt((-8)^2+(-5)^2)
c=sqrt(64+25) = sqrt(89)
300
Find the value of x.
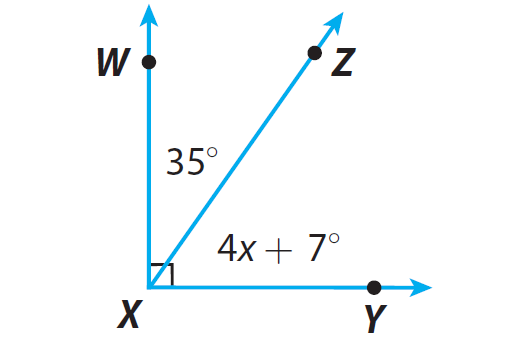
\angleWXZ+\angleZXY=90^o
35+4x+7=90
4x+42=90
4x=48
x=12
400
A line, segment, or ray that cuts an angle or another segment in half.
What is a bisector.
400
Two angles who sum of measures is 90 degrees.
What are complementary angles
400
Two angles that are adjacent and form a straight line together.
What are a linear pair.
400
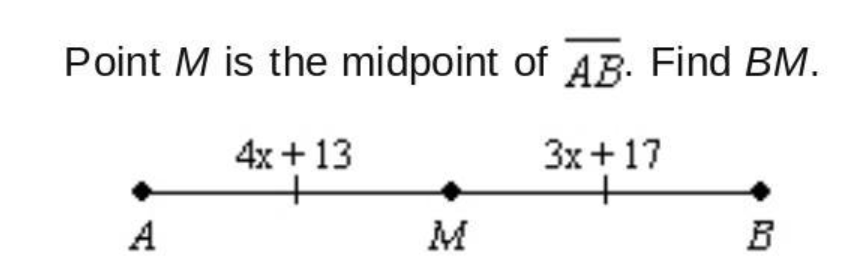
4x+13=3x+17
x=4
BM = 3(4)+17 = 29
400
In the diagram below, OM bisects <AOB. What is the measure of <AOB?
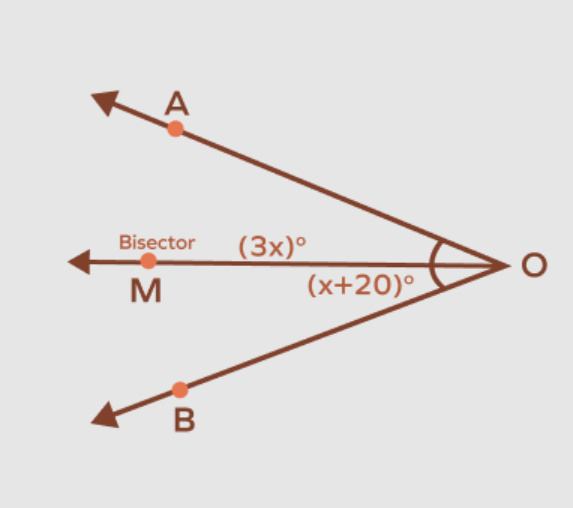
\angleAOM=\angleMOB
3x=x+20
2x=10
x=10
\angleAOB=2(x+20)=2(10+20)=60
500
Formed by two rays that have a common endpoint.
What is an angle.
500
An angle measures 30 degrees, what is the measure of the angles complement?
What is 60 degrees.
500
An angle measures 100 degrees, what is the measure of the angles supplement?
What is 80 degrees.
500
Find the perimeter of polygon ABCD below.
AB = 4
BC: c^2 = 1^2 + 3^2
c^2 = 10
BC = sqrt(10)
CD: c^2 = 2^2+5^2
c^2 = 29
c = sqrt(29)
AD = 1
perimeter: 5+sqrt(10)+sqrt(29)
500
Find the measure of <POS.
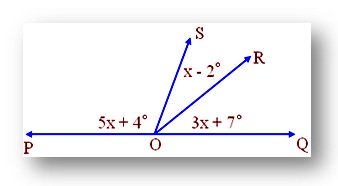
\anglePOS+\angleSOR+\angleROQ=180
5x+4+x-2+3x+7=180
9x+9=180
9x=171
x=19
\anglePOS=5(19)+4=99