the independent quantitative variable
explanatory variable
[Find the Explanatory] daily calorie intake and weight
explanatory: calorie intake
r is always between these two numbers
1 and -1
What is the equation for a regression line?
ŷ = a + bx
How outliers affect the strength of an association?
they weaken/lower strength
What is the formula for determining residuals?
y - haty
the three things you must mention when describing an association
form, direction, strength
[Find the Response] The average income and life expectancy in a sample of countries.
response: life expectancy
Interpret correlation by giving strength and direction
r=-0.936
negative and strong
ŷ=75385 - 0.7455x
x= miles driven
y= price
A truck has driven 38465 miles, predict the price of the truck.
What is $46,709.34
Which of the following shows a strong negative association?
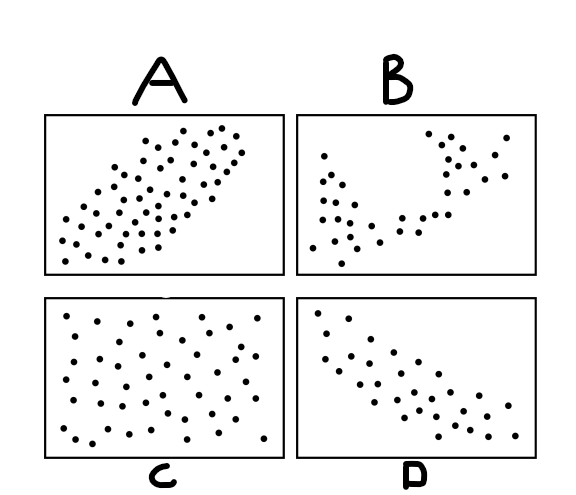
D
Would the circled data point have a negative or positive residual?
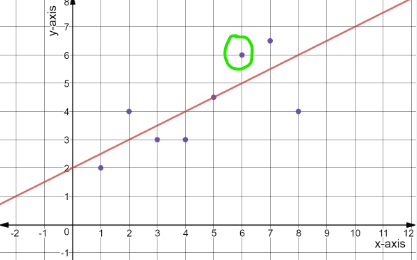
Positive
A measure of the strength and direction of a linear relationship between two quantitative variables represented by the letter 'r'
correlation coefficient
[Find the explanatory] A botanist wants to compare the effect different amounts of fertilizers have on plant growth.
exp: different amounts of fertilizer
What correlation measure is r=0?
no correlation
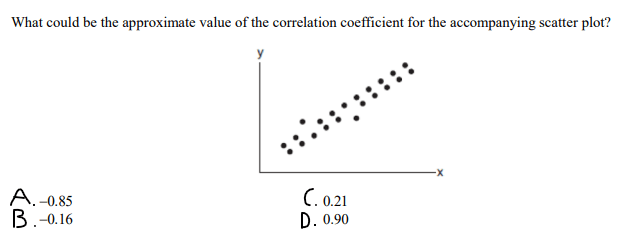
What is the explanatory variable according to the computer output below?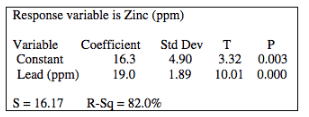
lead (ppm)
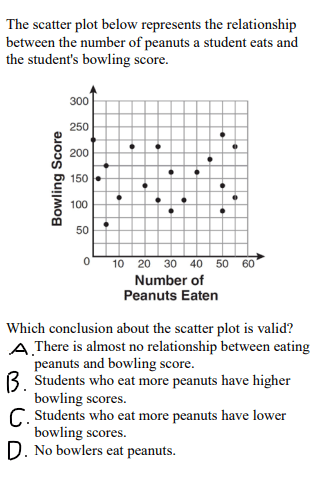
A
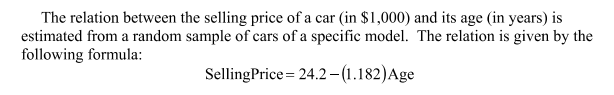
Determine the residual for a car that is 9 years old and actually costs $14,000
$438
using regression line for a prediction outside the range of x-values used to obtain the line is called:
extrapolation
[Find the response] A basketball coach wants to compare the effect that three different training programs have on player's max vertical jump.
response: max vertical jump
D. 0.90
What is the y-intercept in the computer output below?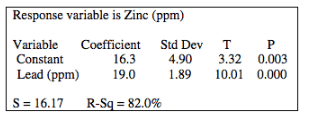
16.3
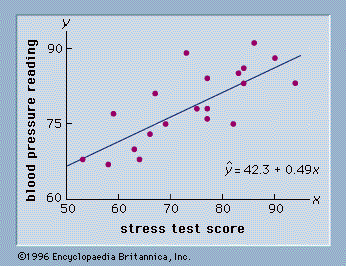
What is the predicted blood pressure for a person with a stress score of 73?
78.07
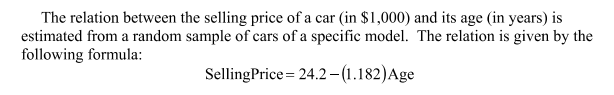
Determine the residual for a car that is 3 years old and actually costs $17,500
A line used to predict possible response values also called a 'line of best fit'
least-square regression line
[Find the explanatory AND the response] amount owed in taxes and annual income
Expl: income
Resp: Taxes
Which value of a correlation coefficient represents the strongest relationship between the two variables in a given linear regression model?
A) -0.96
B) 0.53
C) 0
D) 0.81
A
Write the equation for the least-square regression line given the table below:
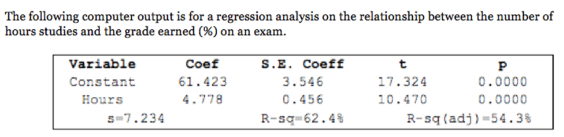
haty=61.423 + 4.778x
A student believes caffeine intake could be associated with exam score. Using the regression analysis below, what would be the predicted exam score for a person who intake 450 mg of caffeine?
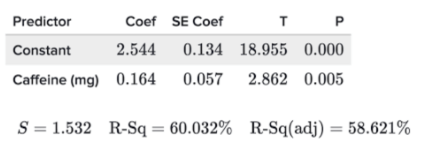
76.344
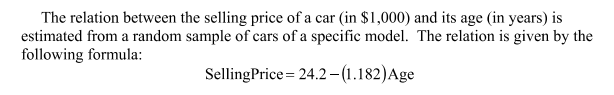
Determine the ACTUAL price of a car that is 6 years old and has a residual of $1202
$18310