Chapters 1 & 2 Review
Recognizing Functions
Domain & Range
Evaluating Functions
Linear Functions (in order)
100
Simplify the expression by combining like terms:
-3x+6+8x-14
5x-8
100
Describe how you would use the Vertical Line Test to tell whether or not a graph represents a function.
Draw a vertical line over the graph. If it crosses that graph at more than one point anywhere on the graph, the graph does not represent a function.
100
The domain of a function is all the possible ___ values;
The range of a function is all the possible ___ values.
x; y
100
Evaluate the function for f(2):
f(x)=3x+1
7
100
The graphs of a linear function always form a straight _____.
Line
200
Simplify the expression by using the distributive property and then combining like terms:
3x+2(4x-6)
11x-12
200
Rewrite the equation below in function notation:
y=2x^2-3x+4
f(x)=2x^2-3x+4
200
DAILY DOUBLE! WAGER THE AMOUNT OF POINTS YOU WOULD BE WILLING TO WIN/LOSE!
Would the domain and range of a continuous function be expressed as an inequality or a list of values? Why?
inequality; fractions/decimals included
200
Evaluate the function for f(-3):
f(x)=abs(2+x)-7
-6
200
Which of these could be the graph of a linear function?
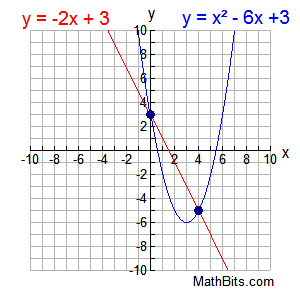
Red
300
Solve the 2-step equation by using inverse operations:
3=x/15+4
x=-15
300
Name all of Santa's Reindeer. Sing your answer for an extra 200 points!
Dasher, Dancer, Prancer, Vixen, Comet, Cupid, Donner, Blitzen, Rudolph
300
A discrete function contains the points (1,2), (3,4), (5,6), (7,8), and (9,10). What is its domain and range?
Domain: {1,3,5,7,9}
Range: {2,4,6,8,10}
300
CHRISTMAS MATH!
You give each of Santa's reindeer 7 carrots. You give Rudolph 4 extra carrots because he has to guide the sleigh through the fog. How many carrots did you give to the reindeer?
67 carrots
300
Calculate the rate of change for the table below. For what variable in slope-intercept form will you plug in this rate of change?
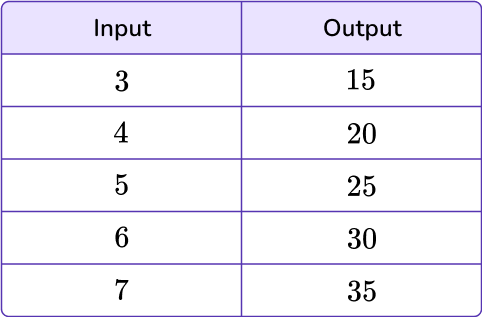
5; m
400
Solve the equation with variables on both sides using inverse operations:
-8(1-4x)=-8+5b
0
400
Sketch an example of both a continuous and a discrete function.
(on board)
400
What is the domain and range of the function graphed below?
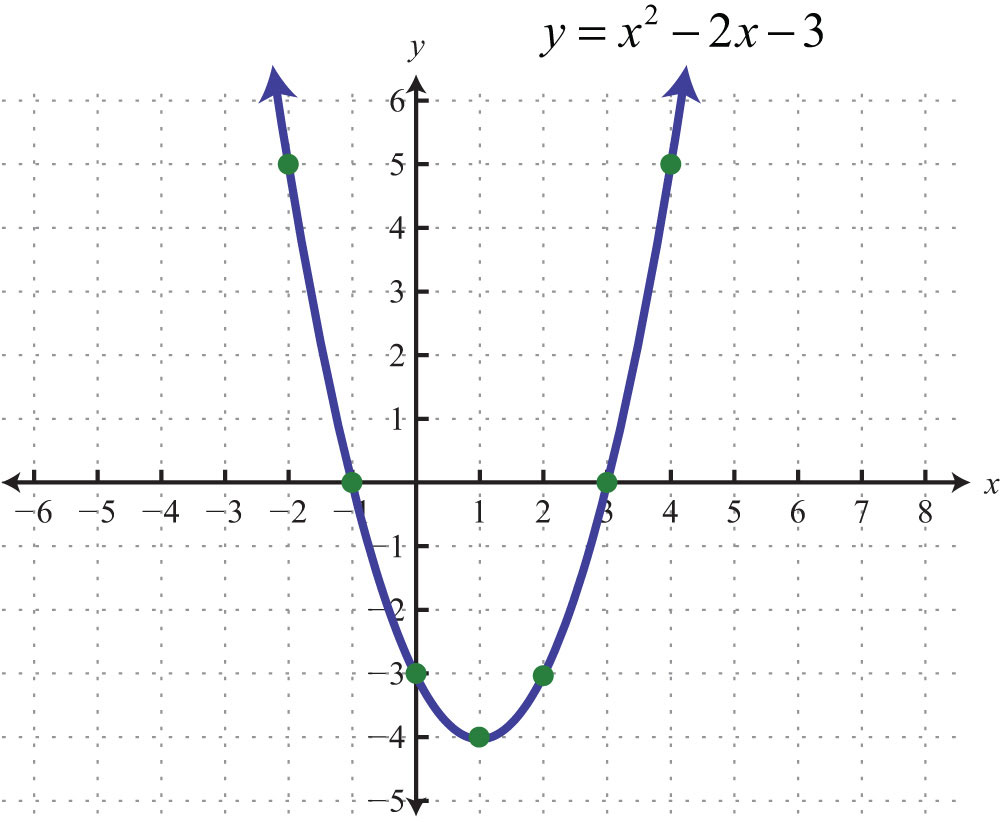
Range:
y> -4
Domain: {all real numbers}
OR
-oo<x<+oo
400
Evaluate the function for f(-6):
f(x)=x^2+10x+24
HINT: If using a calculator, remember to put parentheses around the -6. Remember what happens when you multiply two negative numbers.
0
400
Use one of these methods:
a) find the point (0,y) by extending the table OR by soling for b using a given point and the rate of change from the previous question
to find the y-intercept of the line formed by the information in this table.
0=b
500
Solve the two-step inequality. HINT: Remember what happens to the inequality symbol when you multiply or divide by a negative.
-182<= -9x-2
x<=20
500
Draw an example of:
1) The graph of a straight line that is NOT a function.
2) The graph of a curve that IS a function.
3) A discrete graph that is NOT a function.
1) vertical line
2) parabola, etc.
3) ordered pairs
500
What is the domain and range of the function graphed below?
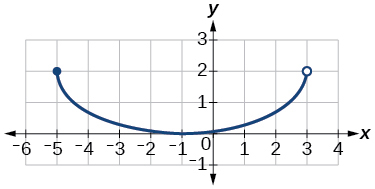
Range:
0<=y<=2
Domain:
-5<=x<3
500
Evaluate the function for f(6)
f(x)=-x^2+6x-3
HINT: Remember to apply the negative AFTER squaring the 6.
-3
500
Use the information from the 300 and 400 point question to write an equation in slope-intercept form that fits the information in the table.
y=5x