Correlations
Explanatory and response variables
Interpreting x and y intercepts
Lucky Dip
100
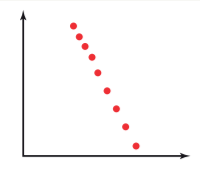
Describe the correlation in terms of direction and strength
Perfect negative linear correlation
100
Determine the explanatory variable from the statement
The age of a motor car and the asking price for the car
Age of a motor car
100
The average rate of change in the response variable for each increase of one unit of the explanatory variable
Gradient
100
3, 5, 7.... name the next prime number in the sequence
11
200
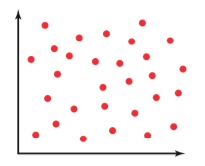
Describe the correlation in terms of direction and strength
Zero correlation
200
Determine the explanatory variable for the following statement
Performance in a team game and lack of sleep
Lack of sleep
200
The value of the response variable when the explanatory is zero
y intercept
200
Name the 8 planets in the solar system
Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune.
300
Describe the correlation in terms of direction and strength
r= -0.7
Moderate negative correlation
300
The variable that goes on the x-axis is:
Explanatory variable
300
Interpret the gradient of the following
predicted shoe size= 0.25 x height -33.4
(height is in cm)
For every increase in 1cm of height, there is an increase of 0.25cm in shoe size.
300
A 10 sided polygon is called
Decagon
400
Describe the correlation in terms of direction and strength
r=0.10
no correlation
400
The variable that goes on the y-axis is:
the response variable
400
Interpret the y intercept for the following
response time = -8.54 x drug dose +45.55
(time is in seconds)
When there is no drug dose administered, response time is 45.55 seconds
400
solve 3x+130 = 250
x = 40
500
To find the correlation coefficient from the coefficient of determination we do this by:
Find the square root of the coefficient of determination
500
What 2 features are important on a scatterplot
accurate scales and labelled axis
500
Interpret the slope and y intercept for the following
Son's height (cm)= 0.54x Father's height (cm) +89.58
For every 1cm increase in father's height, there is a 0.54 increase in son's height. When father's height is zero, son's height is 89.58cm
500
interpret a coefficient of determination of 0.89
89% of the variation in the response variable can be explained by the variation in the explanatory variable