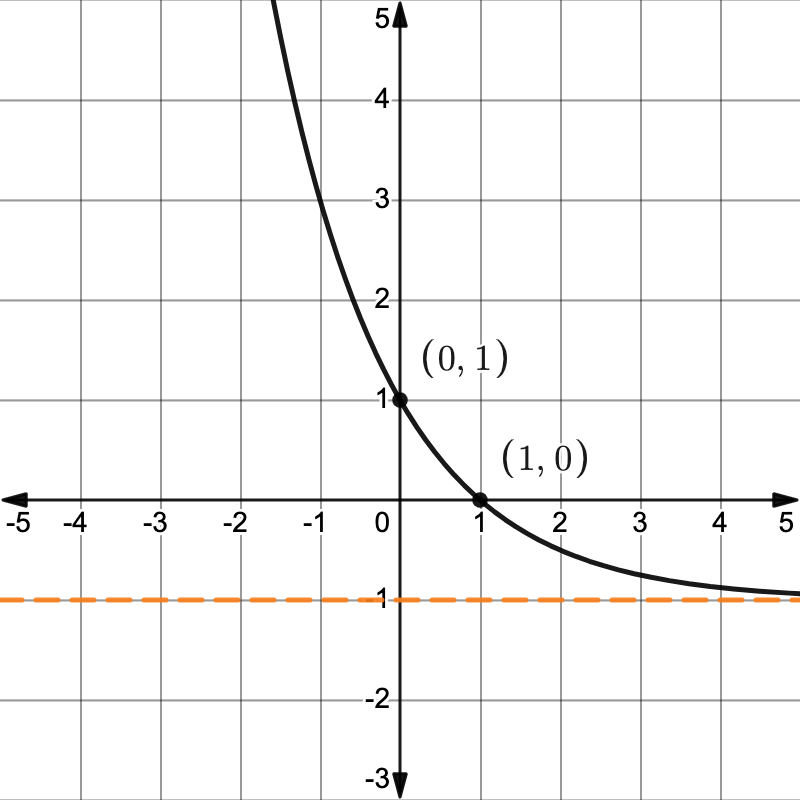
What is the domain, range, asymptotes, and intercepts for (parent) exponential functions
Domain: All reals, Range: y>0, y-int at (0,1), HA at y=0
What is the difference between interest, compounding interest, and continuously compounding interest?
Interest: price paid for borrowing money for a period of time, paid at the end of lending period
Compounding interest: Interest that is charged periodically, every time an interval passes and increases the amount of principal owed
Continuously compounding: interest is charged continuously and constantly added to the principal
What is the domain, range, asymptotes, and intercepts for (parent) logarithmic functions
Domain: x>0, Range: all reals, x-int at (1,0), VA at x=0
A farmer monitoring an insect plague notices that the area affected by the insects is given by A_n=1000\times2^(0.7n) square meters, where n is the number of weeks after the initial observation. Estimate the time taken for the affected area to reach 5000 square meters.
It will take about 3 weeks and 2 days (or when n is about 3.32 weeks)
Condense into a single logarithm
9lnx-3lny
ln (x^9/y^3)
5^(3a)=5^(2a+2)
a=2
Evaluate the function at x=2 , f(x)=1/3\*6^x
f(2)=12
When you were born, your grandparents deposited $5,000 into a college savings account paying 6% continuously compounded interest. What is the balance after 15 years?
$12,298.01
Simplify 12^(log_12(144)
144
Given the below graphs, determine which graph is y=lnx and which is y=ln(x-2) and explain why.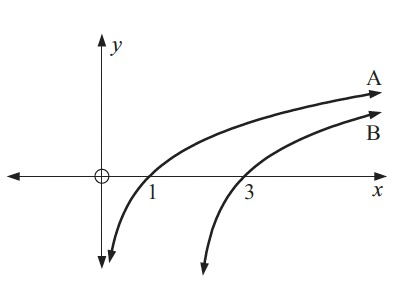
Graph A is y=lnx as the x-intercept is at (1,0)
Without a calculator:
Expand log(6/11)^5
5log6-5log11
log_4(x^2+11)=log_4(-10x+2)
x=-9, x=-1
Evaluate the function at x=-2, f(x)=10\*2^x
f(-2)=5/2
When you were born, your grandparents deposited $5,000 into a college savings account paying 6% continuously compounded interest. How long will it take the balance to reach at least $17,000?
At least 20.396 years
Rewrite log_u(15/16)=x in exponential form
u^x=15/16
You have $5000 to invest in an account that pays 5.2% compounded annual interest. How long will it take for your investment to reach $20,000?
It will take at least 28 years (t=27.3)
Expand
log_8(a/b^5)^5
5log_8a-25log_8b
log_6(x-10)+10=13
x=226
Identify the transformations and graph the parent function and the transformation of:
y=3(1/3)^x
Parent function: y=(1/3)^x
Vertical stretch of 3
A philanthropist pledges to donate 12% of a fund each year. If the fund initially has $654,000.00, how much will the fund have after 8 years?
$235,200.98
without a calculator
Evaluate log_64(4)
1/3
Expand the logarithm
log_8(x/y^6)^4
4log_8x-24log_8y
64^(3x)=16
x=2/9
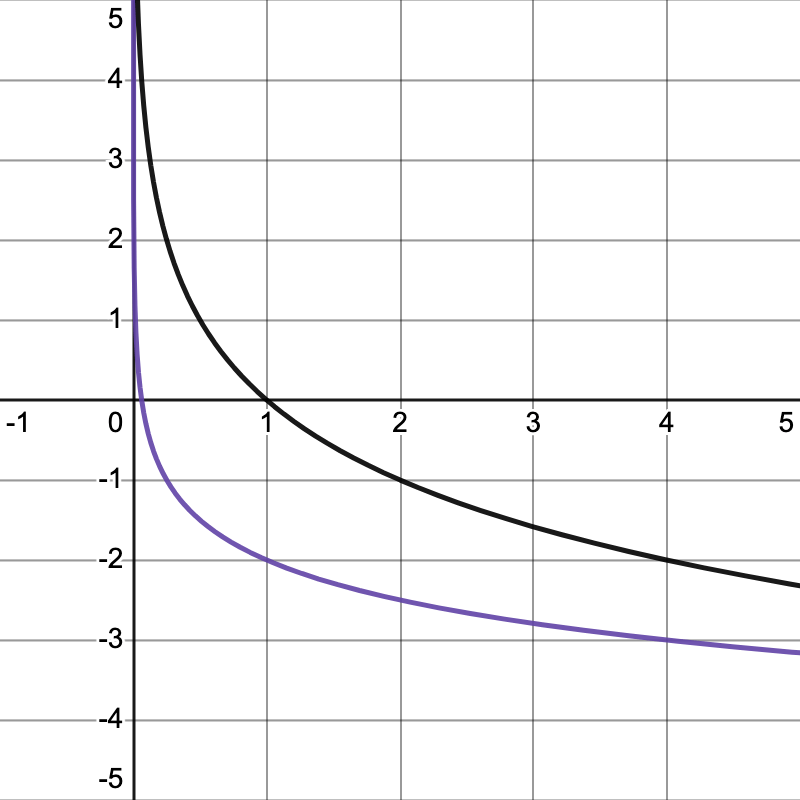
Sketch the graph of the function: y=4\*(1/2)^(x+1)-1
Rentals in a high rise apartment building get more expensive higher up as the views get better. The ground floor (floor 0) the rent is $1,900.00 and the rent increases 3% per floor. What is the rent on the 10th floor?
$2,553.44
Identify the transformations and graph the parent function and the transformation of:
y=1/2\*log_(1/2)x-2
Vertical compression of 1/2, down by 2
The number n of college graduates in thousands after t years can be modeled by n=46log_5(t+3) . Let t=0 represent the year 1985. How many college graduates were there in 2003?
87,017 graduates
Condense into a single logarithm
log_6(11)+log_6(12)/3+log_6(5)/3
log_6(11\root(3)60)
log_2(2x^2-12x)=log_2(-32+x^2)
x=8
Write an equation for the graph below:
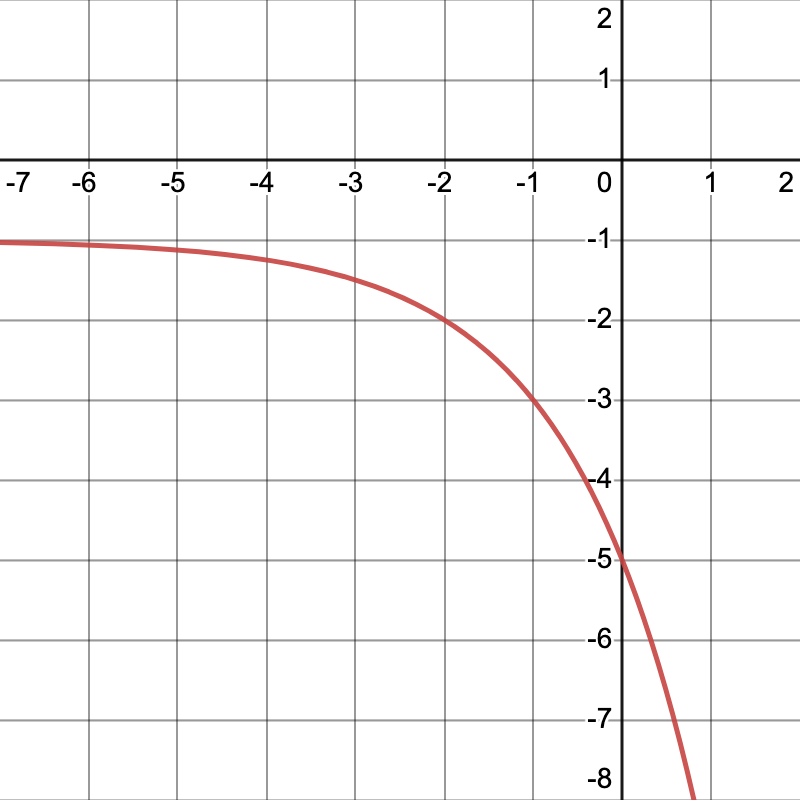
y=-2\*2^(x+1)-1
The radioactive isotope Radium-226 decays exponentially. If the mass was 35625.99 grams 9 thousand years ago and the current mass is 743.10 grams, what will the mass be 7 thousand years from now?
36.63 grams
Find the inverse function of y=log_2(x+5)-9
y=2^(x+9)-5
In 2003, the population of the state of New York was 10.78 million people. in 1990, it was 7.99 million. Using y=ae^(kt) , determine the value of k, New York's relative rate of growth.
k=0.023
Simplify 2(log2x-logy)-(log3+2log5)
log((4x^2)/(75y^2))
log_4(8)+log_4(2x^2)=3
x=2 , x=-2
The below table shows the average salary of baseball players since 1984. What is the estimated salary of a baseball player in the year 2005 to the nearest thousand dollars?
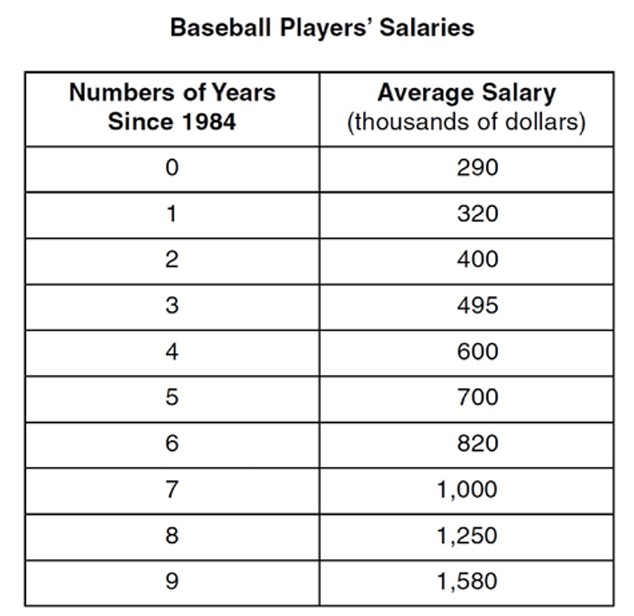
In 2005, it is estimated that a player will earn $14,387,218
Atmospheric pressure decreases exponentially as elevation increases. If the pressure is 31.6 inHg in a valley 0.1 miles below sea level and the pressure at sea level is 31.0 inHg, what is the pressure at 8.0 miles above sea level?
6.69 inHg at 8 miles above sea level
In 2003, the population of the state of New York was 10.78 million people. in 1990, it was 7.99 million.
Nevada's population in 1990 was 14.2 million and can be modeled by y=14.2e^(0.0079t) . Determine when New York's population will surpass Nevada's.
NY will surpass Nevada in 2028 or when t=38.079 years
log_15(x^2-12x)=log_15(-25-2x)
No Solution!