4.1/4.2
Angles and The Unit Circle
Angles and The Unit Circle
4.3/4.4
Trigonometric Functions and Identities
Trigonometric Functions and Identities
4.5/4.6
Graphs of Trigonometric Functions
Graphs of Trigonometric Functions
4.7
Inverse Trigonometric Functions
Inverse Trigonometric Functions
4.8
Real Life Applications
Real Life Applications
100
4.1
pg.333 #5
(-9pi)/15
(a) Sketch the angle in standard position
(b) Determine the quadrant in which the angle lies
(c) List one positive and one negative coterminal angle
(a)
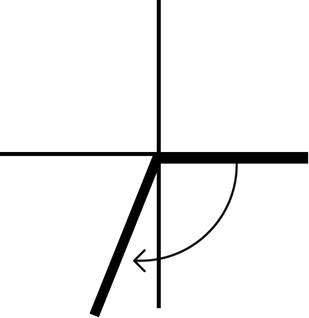(b) Quadrant 3
(c) (21pi)/15, (-39pi)/15
100
4.3
pg. 334 #57
Find the exact values of the six trigonometric functions of the angle theta shown in the figure
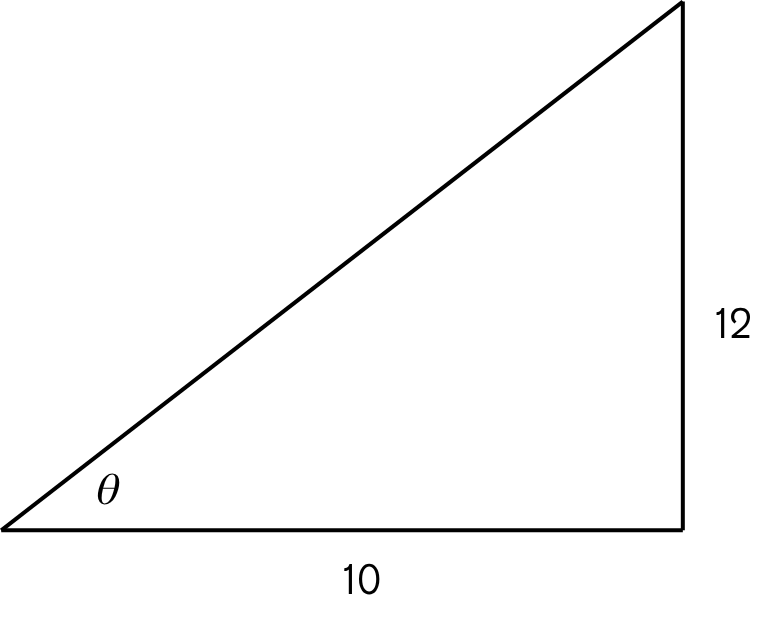
c^2=10^2+12^2=244
c=root()(244)=root()(244)=2root()(61)
sin(θ)=(5root()(61))/61
cos(θ)=(6root()(61))/61
tan(θ)=5/6
csc(θ)=root()(61)/5
sec(θ)=root()(61)/6
cot(θ)=6/5
100
4.5 pg 335 #99
Find the period and the amplitude
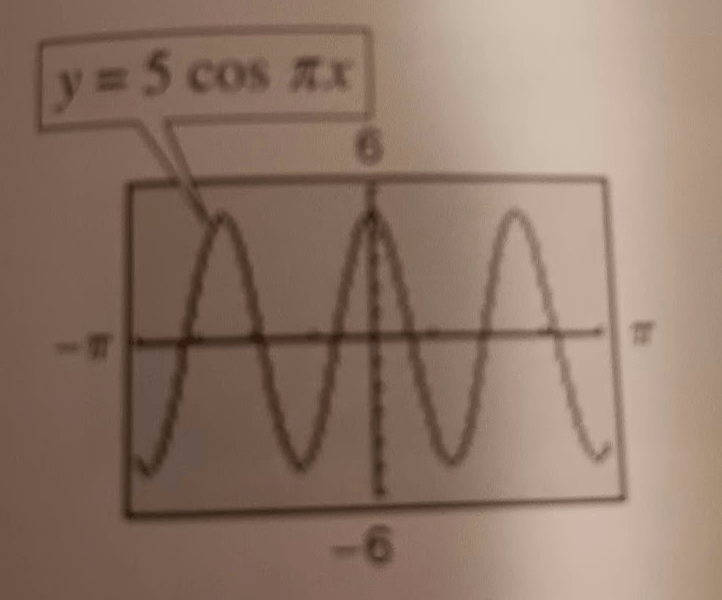
amplitude=5
period=(2pi)/b=(2pi)/pi=2
100
4.7 pg 336 #147
Find the value of the expression without using a calculator
(a) cos^-1(root()(2)/2)
(b)arccos((-root()(3)/2)
(a) pi/4
(b)(5pi)/6
100
A train travels 3.5 kilometers on a straight track with a grade of 1°10'. What is the vertical rise of the train in that distance? (1'=1/60°)
3.5*sin(1 10/60°)=.0713km
200
pg.333 #9
4.1
Find the complement and the supplement of the angle
(3pi)/10
Complement
pi/2-(3pi)/10=(5pi)/10-(3pi)/10=(2pi)/10=pi/5
Supplement
pi-(3pi)/10=(10pi)/10-(3pi)/10=(7pi)/10
200
4.3
pg. 334 #61
Use trigonometric identities to transform one side of the equation to the other.
cscθtanθ=secθ
cscθtanθ=(1/sinθ)(sinθ)/cosθ=1/cosθ=secθ
200
4.5
Find a, b, and c for the function
y=acos(bx-c)
so that the graph matches the graph below
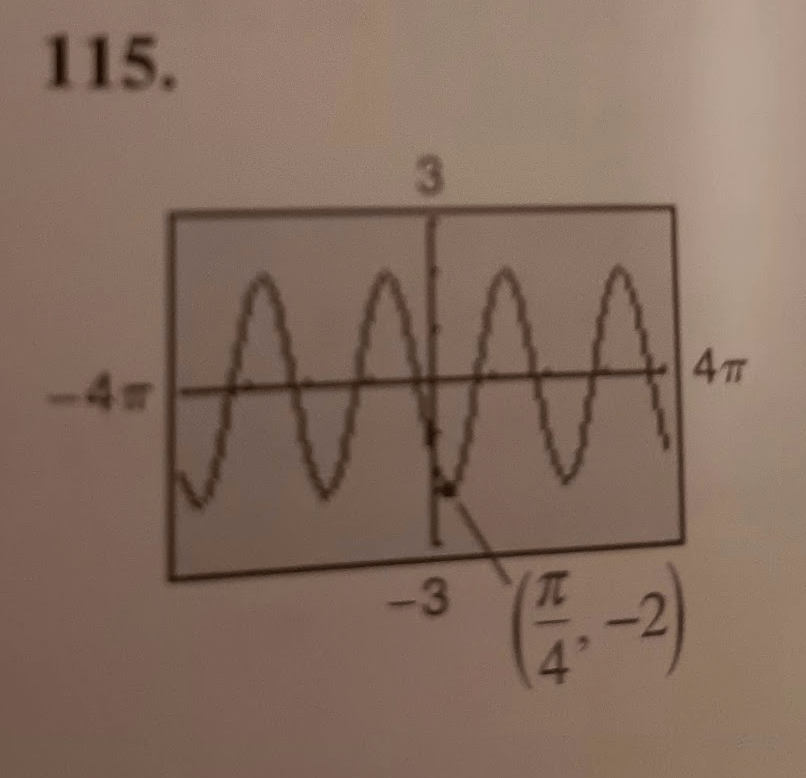
flipped over x-axis and magnitude of 2 so
a=-2
cosine function shifted to the right pi/4 so
c=pi/4
period is twice within 4pi so
period=2pi
b=1
y=-2cos(x-pi/4)
200
4.7pg336#157
Use the inverse trigonometric function to write theta as a function of x
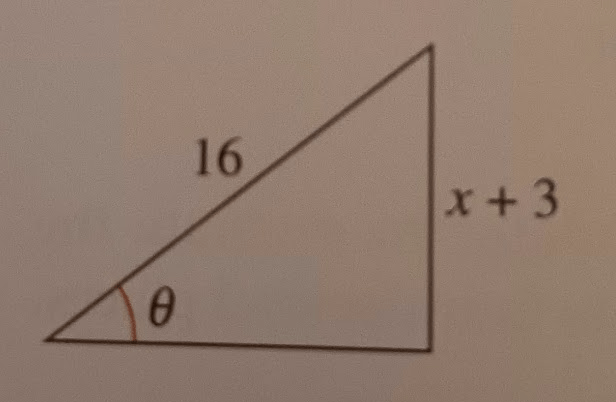
sin^-1((x+3)/16)=theta
200
4.8 pg 331 #65
The tables shows the average sales S (in millions of dollars) of a outerwear manufacturers for each month t, where t=1 represents January.
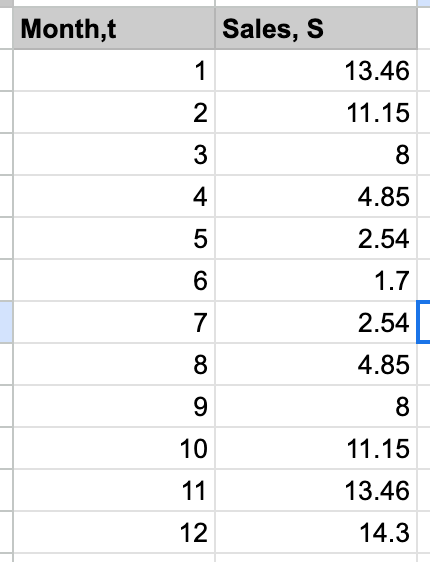
(a) create a scatter plot for the data
(b) Find a trigonometric models that fits the data, and write the equation.
(c) What is the period of this function? Do you think it is reasonable given the context?
(d) Interpret the meaning of the model's amplitude in the context of this problem.
(b) y=8+6.3sin(.524x+1.57)
"period"=(2pi)/b=(2pi)/.524=12
(c)It makes sense because the period is 12 months or a year
(d)It fluctuates 6.3 million dollars of sales in a year from the average sales of 8 million dollars.
300
4.2
pg334 #45
Evaluate the six trigonometric functions of the real number t, as well as the point on the unit circle that corresponds to the real number t.
t=(7pi)/6
sin((7pi)/6)=-1/2
cos((7pi)/6)=(-root()(3))/2
tan((7pi)/6)=(root()(3))/3
csc((7pi)/6)=-2
sec((7pi)/6)=(-2root()(3))/3
cot((7pi)/6)=root()(3)
300
4.4
pg335 #81
Find the reference angle θ' and sketch θ and θ' in standard position.
θ=(-6pi)/5
(6pi)/5-pi=pi/5
300
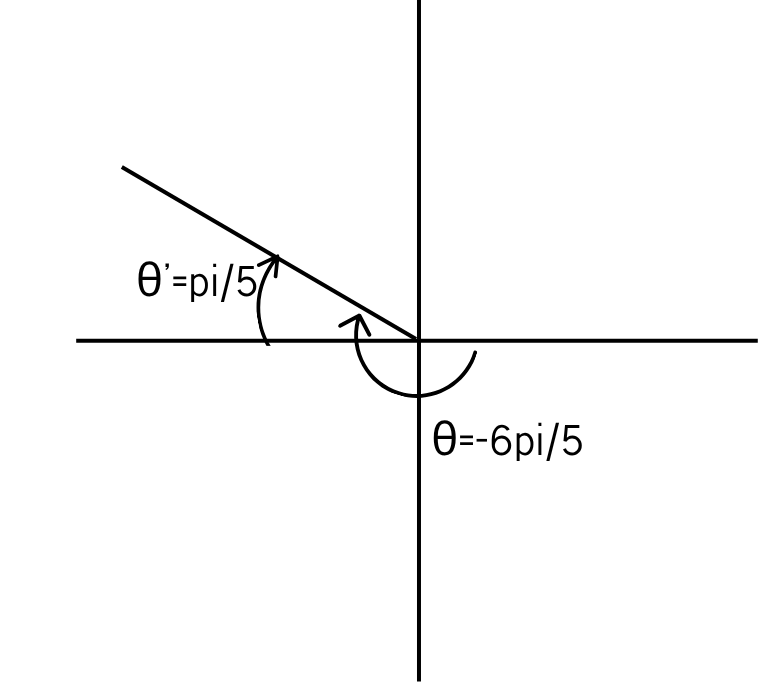
4.6 pg 336 #123
Sketch a graph of the function. Include two full periods.
y=1/4tan((pix)/2)
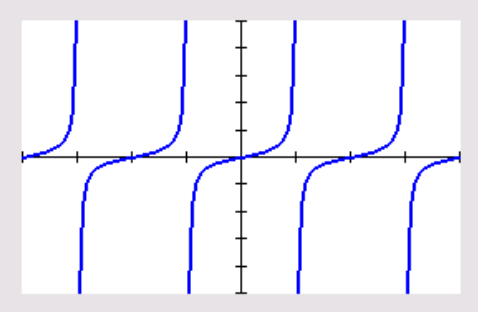
"amplitude"=1/4
"period"=pi/b=pi/(pi/2)=2
300
4.7pg336#158
Use the inverse trigonometric function to write theta as a function of x
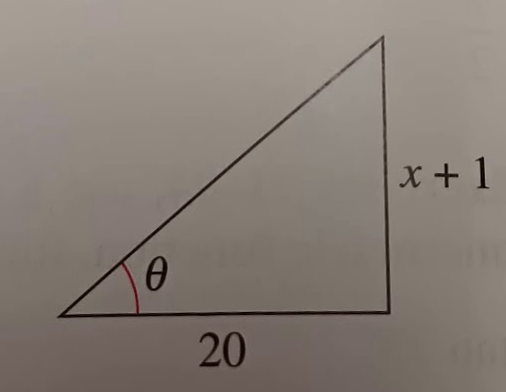
tan^-1((x+1)/20)
300
4.8 pg 337 #167
A buoy oscillates in simple harmonic motion as waves go past. At a given time, it is noticed that the buoy moves a total of 6 feet from its low point to its high point, returning to its high point every 15 seconds(see figure). Write an equation that describes the motion of the buoy if it is at its high point at t=0.
We will need to construct a trigonometric function and find the values of a and b.
Amplitude (a) will be the difference in highest point and the lowest point and divided by two. Or the Highest point/lowest point and equilibrium.
a=(P_1-P_2)/2=6/2=3
The period will be when it completes a full cycle, so that is given as 15 seconds. To find b in the equation, we need to work backwards with the equation for period.
Period=(2pi)/b=15 "seconds"
15b=2pi
b=2pi/15=.4189
Then we will need to choose a trigonometric function from sine or cosine. Since at t=0 the buoy starts at its highest point we will choose cosine based on knowledge of cosine's graph.
Then plug in a and b to get
f(x)=acos(bx)=3cos(.4189x)
400
pg 333 #29 & #31
Convert (a) from degrees into radians
Convert (b) from radians into degrees
(a) -33 deg
(b) (5pi)/7
(a) -33deg * (pi rad)/(180 deg)=(-33pi rad)/180=-0.183 rad=.576 rad
(b) (5pirad)/7 * (180 deg)/(pi rad)=(900 deg)/7=128.57 deg
400
4.4
pg. 335 #85
Evaluate the sine, cosine, and tangent of the angle without using a calculator.
θ=-210 deg
-210 + 360 = 150 deg
The terminal side will be in the second quadrant.
180-140=30 deg
The terminal side will make a 30-degree angle with the x axis, so
sin(30)=1/2
cos(30)=root()(3)/2
tan(30)=root()(3)/3
Now we know that -210 will be in the second quadrant so we need to adjust the signs so
sin(-210)=1/2
cos(-210)=-root()(3)/2
tan(-210)=-root()(3)/3
400
4.6 pg336 #137
Sketch a graph of the function. Include 2 full periods.
y=2sec(x-pi)
"amplitude"=2
"period"=(2pi)/b=(2pi)/1=2pi
"shift"=pi="shift to the right "pi
400
4.7 pg336 #159
Write an expression that is equivalent to the expression.
sec[arcsin(x-1)]
Let's assume that
x-1=(x-1)/1
That way we know that x-1 is the opposite side of the triangle and 1 is the hypotenuse
The triangle can be shown here
To find the last side b, use the pythagorean theorem
(x-1)^2+b^2-=1^2
x^2-2x+1+b^2=1
b^2=2x-x^2
b=root()(2x-x^2)
Now we can assume that angle y can be substituted into the original equation
angle y=arcsin((x-1)/1)
sec(angley)=1/cos(angley)=1/(b/1)=1/root()(2x-x^2)=(root()(2x-x^2))/(2x-x^2)
400
4.1 pg 333 #40
A car is moving at a rate of 28 miles/ hour, and the diameter of the wheels is about 2-1/3 feet.
(a) Find the number of revolutions per minute the wheels are rotating
(b) Find the angular speed of the wheels in radians per minute.
(a)
("circumference")/"revolution" ="ft"/"rev" =2*pi*r=2*d=2.333pi "ft"/"rev"" or " (1 " rev")/(2.333pi" ft")
28 "miles"/"hour"*(5280" ft")/(1" mile")*(1 "hour")/(60 " min")=2464 "ft"/min
2464 "ft"/"min" * (1" rev")/(2.33pi " ft")=336 "rev"/"min"
(b)
1 "revolution" = 2pi " radians"
336 "rev"/"min"*(2pi " radians")/(1"rev")= 2115 "radians"/"min"
500
4.1
pg 333 #39
The radius of a compact disc is 6 centimeters. Find the linear speed of a point on the circumference of the disc if it is rotating at a speed of 500 revolutions per minute.
"linear speed" = "arc length"/"time"
1" revolution" = "circumference"=2pir=2*pi*6=12pi "centimeters"/"revolution"
12pi "centimeters"/"revolution"*(500" revolutions")/"min"= (6000pi" centimeters")/"min"=(18849.56" centimeters")/"min"
500
4.3 pg 334 # 67
An engineer is trying to determine the width of a river. From point P, the Engineer walks downstream 125 feet and sights to point Q. From this sighting, it is determined that θ=62 deg. How wide is the river?
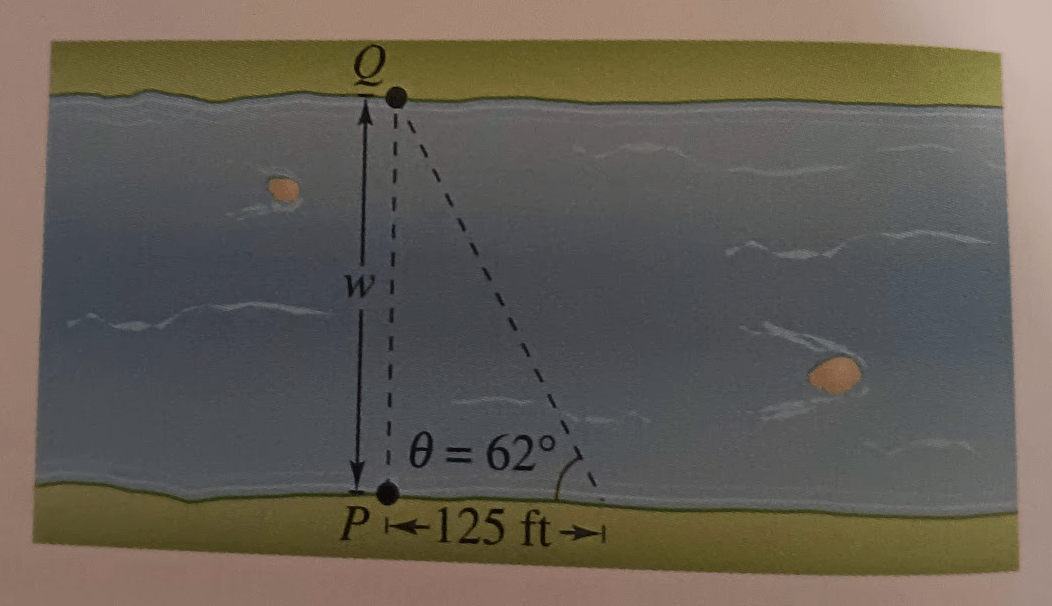
tan(62)=w/125
125*tan(62)=w=235.09 ft
500
4.5 pg 336 #119
Use your calculator to graph the sales function over 1 year, where S is the sales (in thousands of units) and t is the time (in months, with t=1 corresponding to January. Determine the months of maximum and minimum sales.
S=48.4-6.1cos((pit)/6)
Maximum Sales - June
Minimum Sales - December/January
500
4.7 pg336 #161
Write an expression that is equivalent to the expression.
sin(arccos((x^2)/(4-x^2)))
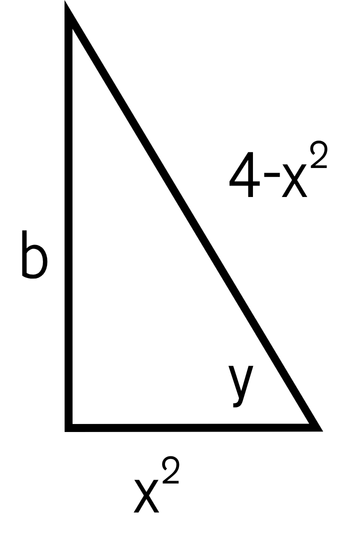
angle y = arccos(x^2/(4-x^2))
From a triangle you use the Pythagorean theorem to find the last side of the triangle b
b^2+x^4=(4-x^2)^2
b^2=-x^4+x^4-8x+16=16-8x
b=root()(16-8x)=2root()(4-2x)
sin(arccos(x^2/(4-x^2)))=sin(y)="opp"/"hyp"=(2root()(4-2x))/(4-x^2)
500
A passenger in an airplane flying at an altitude of 37,000ft sees two towns directly to the west of the airplane. The angles of depression to the towns are 32° and 76° (see figure). How far apart are the towns?
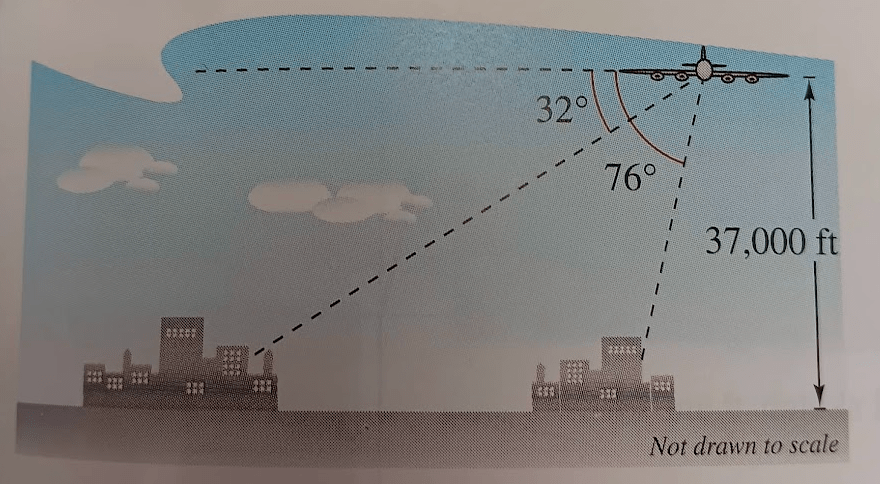
We need to first find some angle measurements. Based on what we are given, we can determine the angle from the first town to a vertical line from the airplane (90-76) and the smallest triangle to be 14 deg.(pic below)
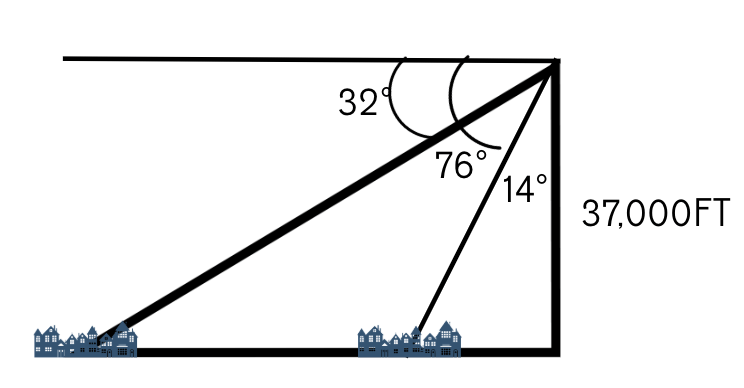
Based on that we can find the horizontal distance from the airplane to the first town to be.
tan(14°)=(x_1)/37000
x_1=37000*tan(14°)=9225.14ft
Then we need to find the top angle of the triangle formed from the airplane, the second town, and a vertical line from the airplane. (pic below)
76°-32°=44°
44°+14°=58°
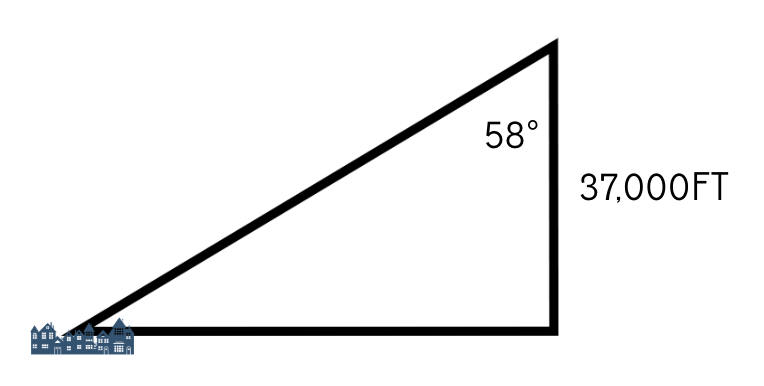
We can then find the horizontal distance from the second town to the airplane as
tan(58°)=(x_2)/37000
x_2=37000*tan(58°)=52841.48
Then we need to take the difference between the two x's to find the distance between the two towns.
x_2-x_1=52841.48-9225.14=43616.48ft