4.1 Coordinates and Distance
4.2 Polygons and Congruence
4. 3/4.6 ASA, SAS, and SSS
4.4 Congruence Proofs
4.5 Isosceles and Equilateral Triangles
100
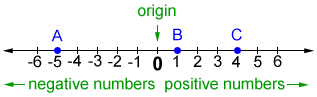
Draw a one dimensional coordinate system. Label the axis, the origin, and an example point.
100
What is a polygon?
A connected set of at least 3 line segments in the same plane, such that each segment intersects two others, one at each endpoint.
100
Give an example of an opposite side and an opposite angle.
there are three possible answers
∠ABC is opposite side AC and vice versa
∠BCA is opposite side AB and vice versa
∠BAC is opposite side BC and vice versa
100
What theorem would you use to prove these triangles are congruent?
SSS
100
What is a scalene triangle?
A triangle where no sides are equal. It has three unique sides.
200
Draw a 2d Coordinate System. Label the origin, the axes, the quadrants, and a sample point.
200
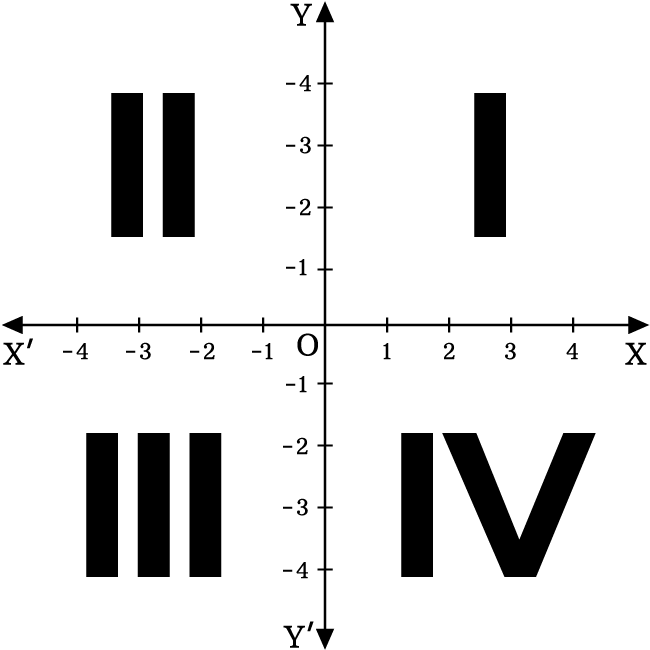
A triangle with 15 sides is called what?
15-gon
200
Give an example of an included angle and side
There are many answers.
Side AB is included in angles ∠CBA and ∠CAB
∠ABC is included in sides AB and BC
200
Can we prove that these triangles are congruent? If so what theorem would you use? And how?
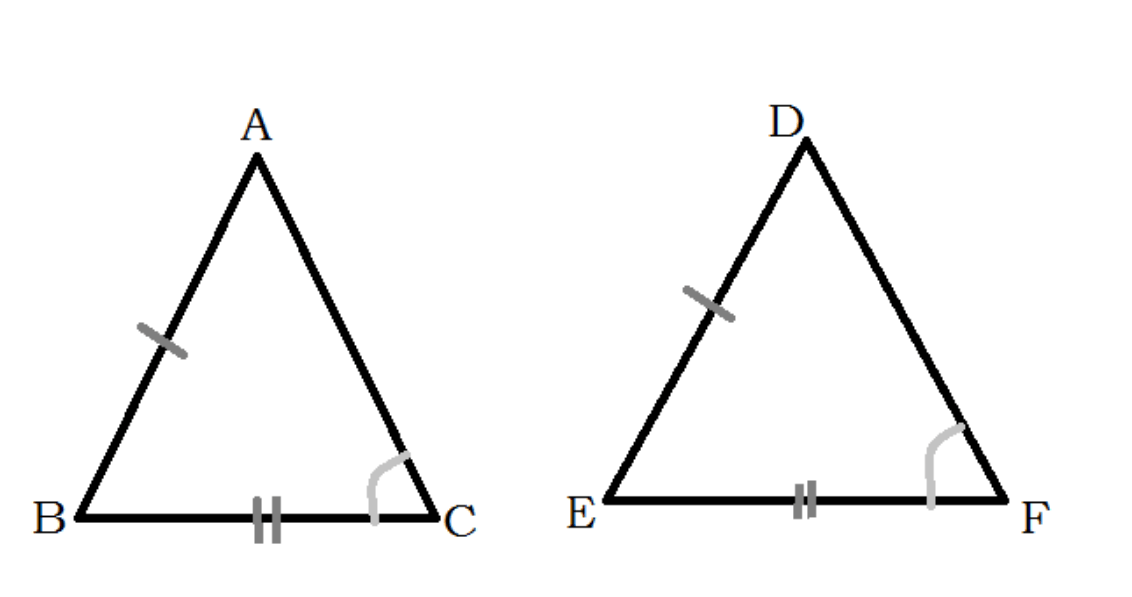
No you cannot the angle needs to be included within the two sides to use SAS. Here is an example of how these triangles could be drawn if we do not know the other angles or side.
200
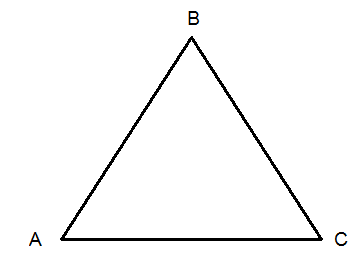
True or false? Are Equilateral triangles Equiangular? Why or Why not?
True or false? Are Equiangular triangles Equilateral?
Why or Why not?
True due to SSS we know that triangles are congruent.
False we do not know for certain. Think about a little triangle and just a larger scale of that triangle it will have the same angles but different size sides.
300
What is the distance formula?
d=root()((x_2-x_1)^2+(y_2-y_1)^2)
300
What do congruent and corresponding mean and how are they related with triangles?
Congruent - identical in form; coinciding(corresponding) exactly when superimposed.
Corresponding - parts of shapes that are in the same relative position to one another
Corresponding sides and angles of congruent triangles are congruent.
300
How many corresponding parts (sides and/or angles) of two triangles do you need to prove that they are congruent?
Three parts of a triangle are needed to prove congruence. Eg. SAS, SSS, ASA. One of them needs to be a side.
300
Given: △TUV ≅ △DFE based on what theorem?
Find x
They are congruent base on ASA or SAS!
2x+20=34
2x=14
x=7
300
Is an equilateral triangle an isosceles triangle? Why and what is the definition of both?
Yes, an isosceles triangle has two equal sides, an equilateral triangle has 3 equal sides, so it also has two equal sides.
400
Use the distance formula to find distance between points at (6,4) and (2,1). Hint: Drawing a picture may help
d=root()((6-2)^2+(4-1)^2)=root()(4^2+3^2)=root()(16+9)=root()(25)=5
400
How many type of congruent polygons are there and how many of each.
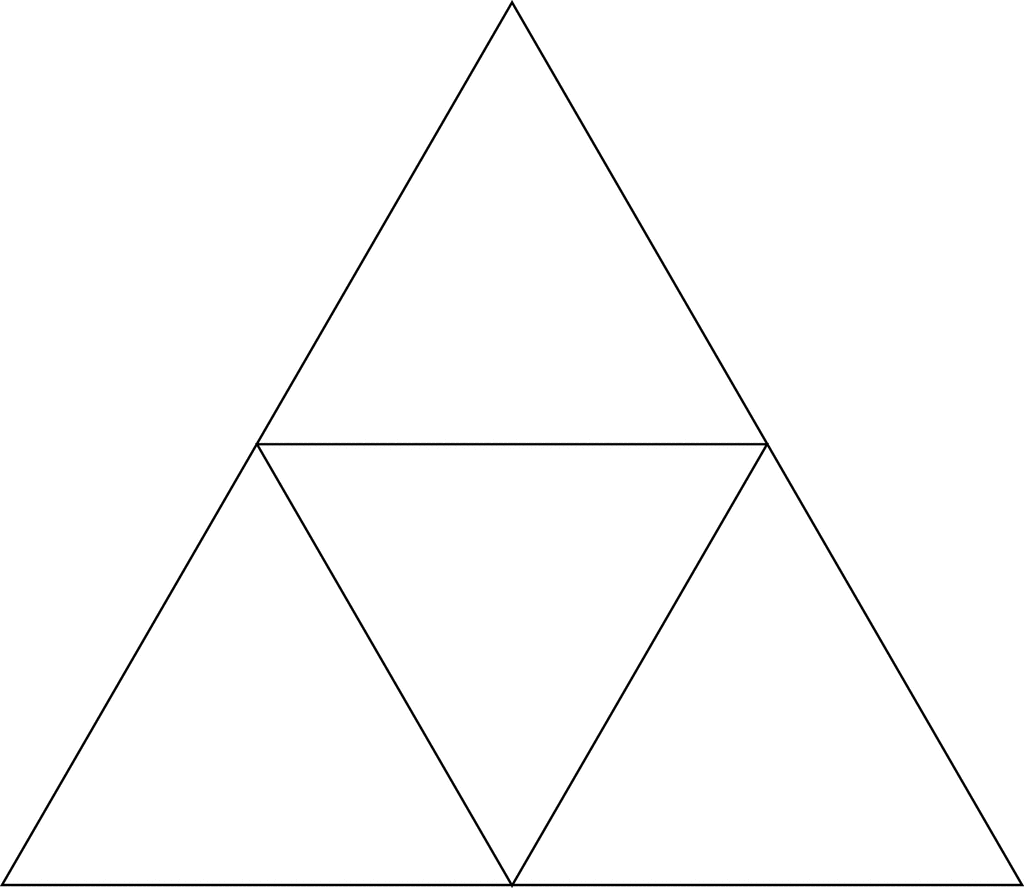
4 small triangles
3 trapezoids
3 rhombuses
400
True or False? I can prove that two triangles are congruent if I know that all three pairs of their corresponding angles are congruent.
False
You need to know at least one pair of corresponding sides of a triangle to prove congruence. You cannot have AAA.
400
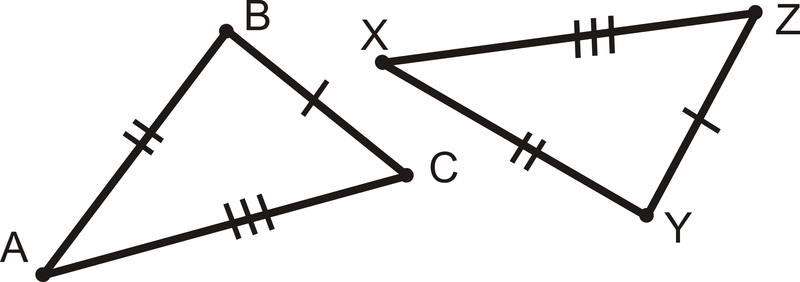
What theorem would you use to prove congruence with these two triangles? And show how.
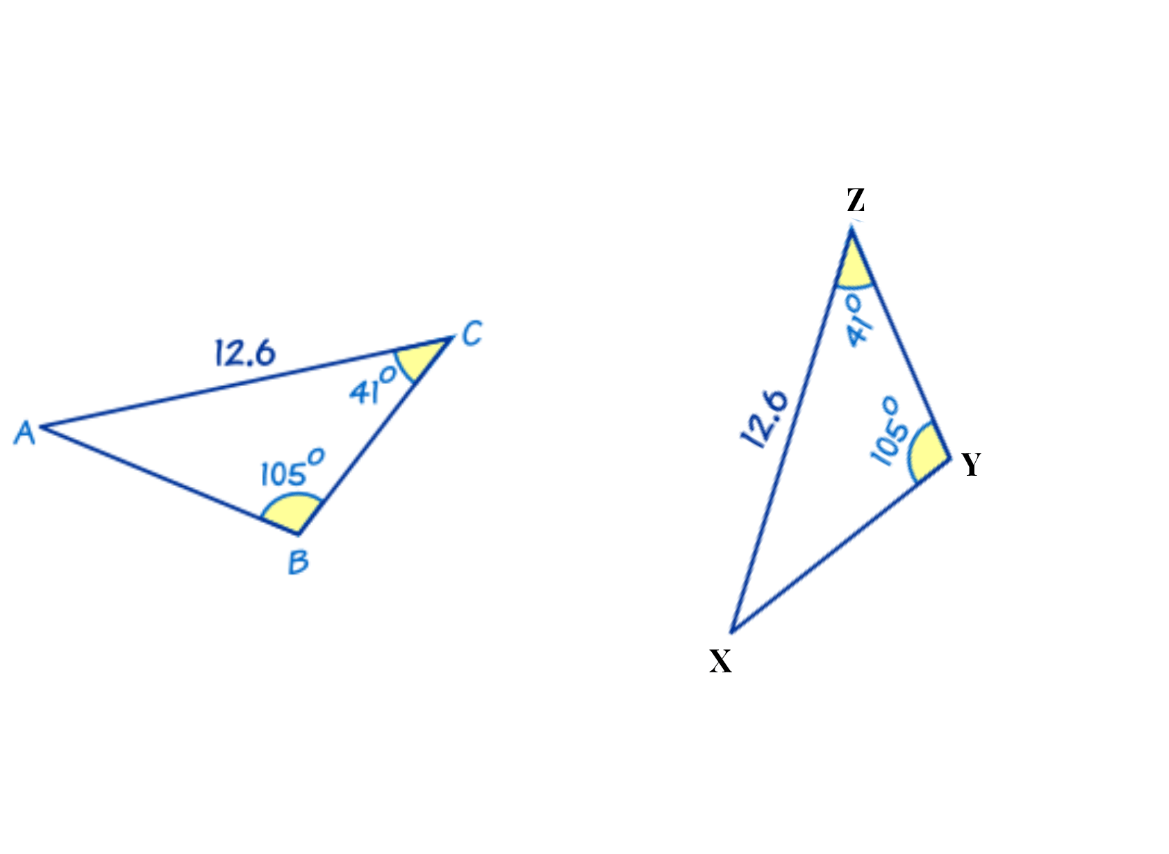
ASA -
You can find the ∠CAB by knowing the sum of the angles of a triangle equals 180. So ∠CAB and ∠ZXY = 180-(105+41)=180-146=34.
Then ∠CAB=∠ZXY, AC=XY, and ∠BCA=∠YZX so △ABC is congruent to △XYZ by ASA
400
Below is an isosceles triangle, △ABC. What do we know about the angles ∠ABC and ∠ACB? Why?
∠ABC = ∠ACB because opposite angles of congruent sides in an isosceles triangle are equal using the isosceles triangle theorem.
500
Use the distance formula to find the sides of the triangle below.
A - (-1,1)
B - (1,4)
C - (3,3)
AB = root()((-1-1)^2+(1-4)^2)=root()((-2)^2+(-3)^2)=root()(4+9)=root()(13)
BC = root()((1-3)^2+(4-3)^2)=root()((-2)^2+(1)^2)=root()(4+1)=root()(5)
CA = root()((3-(-1))^2+(3-1)^2)=root()((4)^2+(2)^2)=root()(16+4)=root()(20)
500
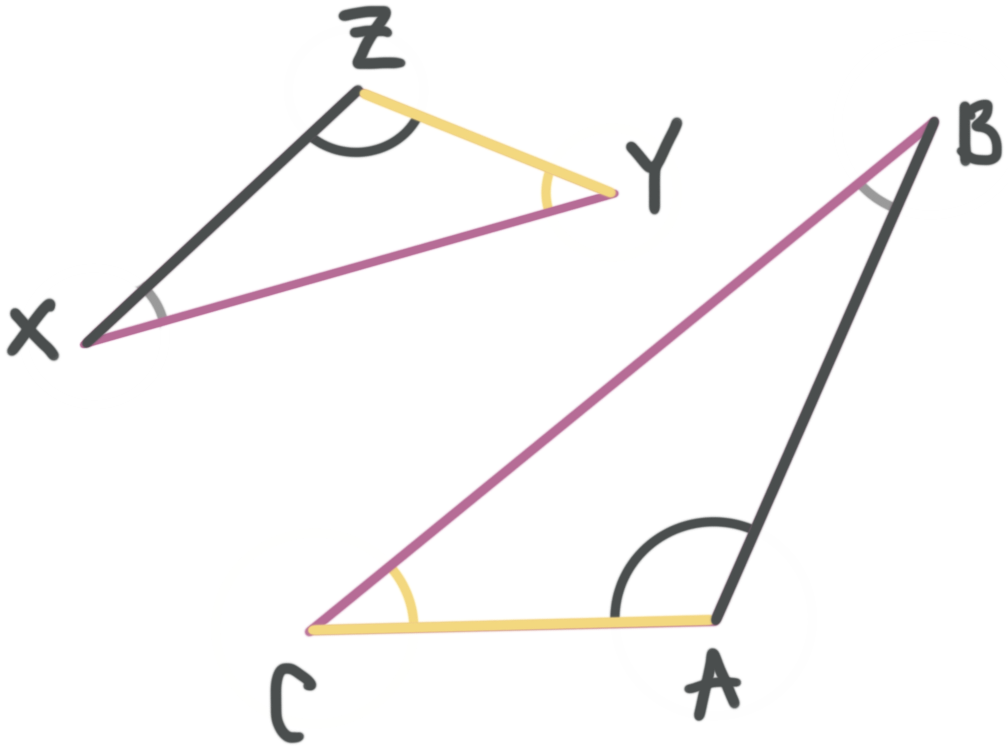
What angles and sides are corresponding in the following two triangles?
AC ≅
ZY
AB ≅ ZX
BC ≅ XY
∠ABC ≅ ∠ZXY
∠BAC ≅ ∠XZY
∠ACB ≅ ∠ZYX
500
What does ASA, SAS, and SSS mean and what are they used for? Why are ASA and SAS in that order? (not AAS or SSA)
They are used to prove that two triangles are congruent and stand for
ASA-Angle Side Angle
SAS- Side Angle Side
SSS - Side Side Side
For ASA and SAS they have to be in that order so that the side in ASA or the angle in SAS is included between the other two.
500
Write the proof for the cowboy problem.
Prove: CE = AD
Given: CA⊥AD, CB=BA, ∠C is a right angle and ∠CBE and ∠DBA are vertical angles
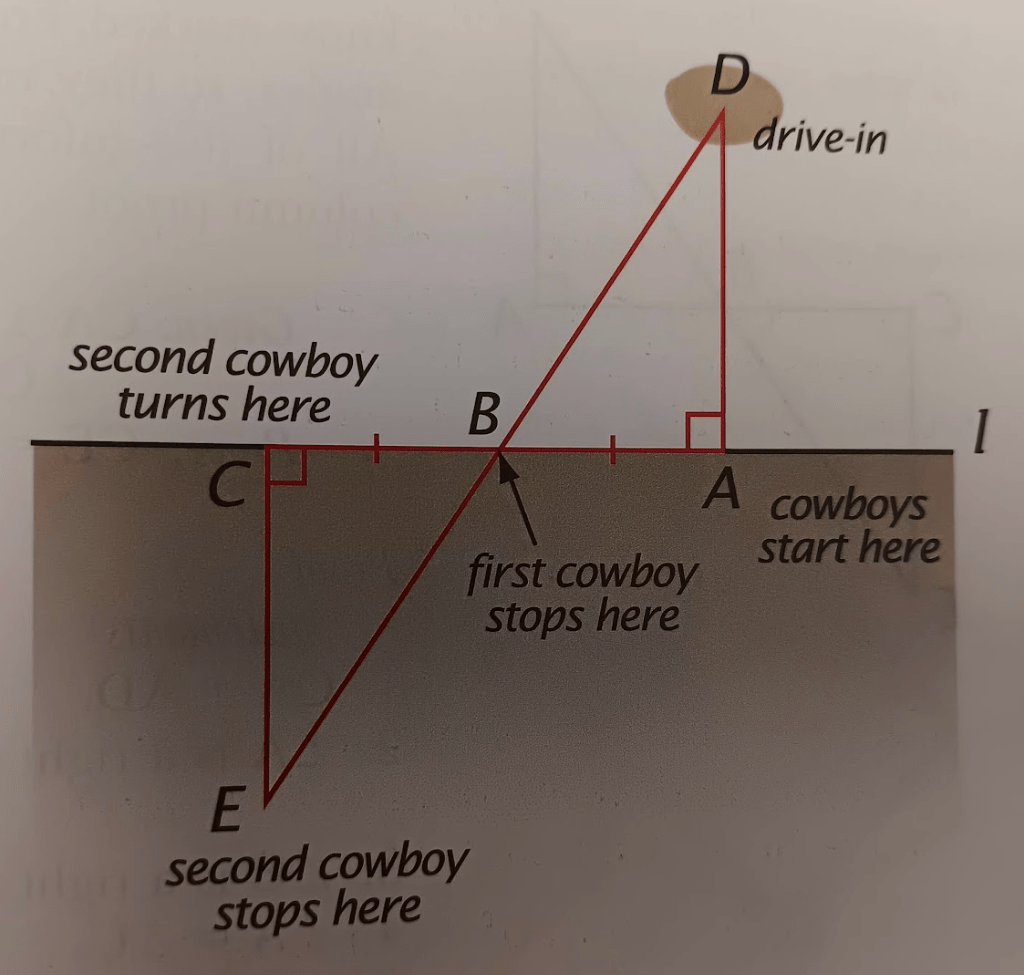
1. CA⊥AD. - Given
2. ∠A is a right angle - perpendicular lines form right angles
3. ∠C is a right angle - Given
4. ∠A=∠C - All right angles are equal
5. ∠CBE and ∠DBA are vertical angles - Given
6. ∠CBE = ∠DBA - vertical angles are equal
7. CB=BA - Given
8. △CBE≅△ABD - ASA
9. CE = AD - Corresponding parts of congruent triangles are equal
500
Find the ∠ABC, ∠BCA, and ∠CAB of △ABC. What type of triangle is it? Write it like a proof.
Given:
OA bisects ∠CAB and OB bisects ∠ABC
AO=OB
∠AOB = 120
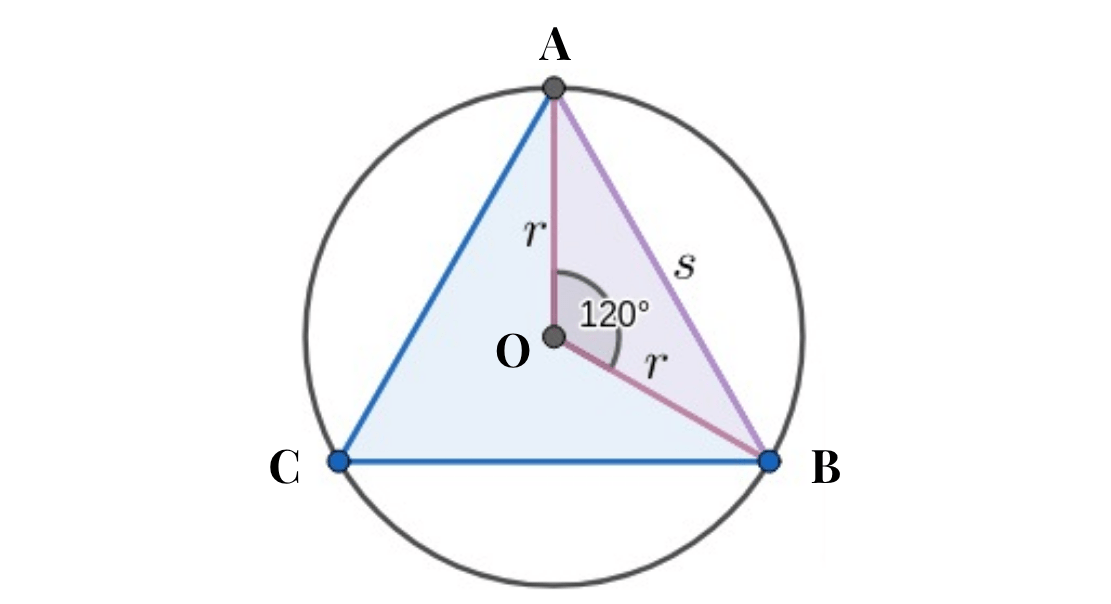
Proof
∠AOB = 120 - Given
∠AOB + ∠OAB + ∠OBA = 180 -The sum of the angles of a triangle =180
AO=OB - Given
△AOB is an isosceles triangle - definition of isosceles triangle
∠OAB=∠OBA - Isosceles Triangle Theorem
∠AOB + 2(∠OAB) = 180, ∠OAB=30 - substitution and subtraction and division.
OA bisects ∠CAB and OB bisects ∠ABC - Given
∠CAO=∠OAB and ∠CBO=∠OBA and ∠CAO+∠OAB=∠CAB and ∠CBO+∠OBA=∠CBA - bisect angle theorem and betweeness of angles theorem
30+30=60=∠CAB and 30+30=60=∠CBA - substitution and addition
∠CAB+∠CBA+∠BCA=180 and 60+60+∠BCA=180 and ∠BCA = 60 - Substitution, Addition, and Subtraction.
△ABC is an equiangular triangle - ∠ABC = ∠BCA = ∠CAB