Ruler and Distance/Protractor and Angles
Bisection/Extra
Complementary and Supplementary Angles
Linear Pairs and Vertical Angles
Perpendicular and Parallel Lines
100
What is the difference between a ruler and a straight edge?
A Straight edge is something straight
A Ruler is a straight edge with measurement
100
What is the point that divides a line into two equal segments?
A midpoint
100
If angles are complements, what can you say about the relationship between their angles?
They add up to be 90 degrees.
100
Vertical angles are formed from what?
Two intersecting lines
100
What are the characteristics of perpendicular lines?
Two lines that form a right angle
200
What equation follows from the following statement?OA-OB-OC
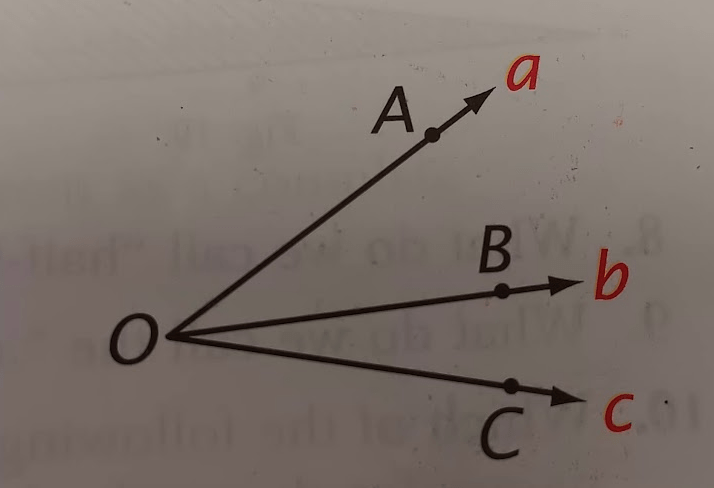
From the betweenness of rays theorem
OA-OB-OC iff ∠AOB+∠BOC=∠AOC
Answer
∠AOB+∠BOC=∠AOC
200
What does bisection of a angle mean?
a line divides the angle into two equal parts
200
Complementary angles need to touch, true or false?
False
200
The angles of a linear pair have what type of relationship?
They are supplements of each other (supplementary angles).
200
What are the characteristics of parallel lines?
1. They do not intersect (same slope)
2. They are in the same plane
300
Finish the following statement
A point is between two other points on the same line IFF_________
Its coordinates are between their coordinates
300
What is a corollary
A theorem that can easily proved as a consequence of a postulate or another theorem
300
If two supplementary angles are added together, what shape do you get?
A straight line
300
What is the value of x?
5x+10=105
5x=95
x=19
300
You have four adjacent angles (angles that are next to each other and share lines) that add up to 360 degrees (∠1+∠2+∠3+∠4).
Two of them are 90 degrees.
Do you have any vertical angles?
Do we know the value of the other two angles?
No we could have the following situation
∠1+∠2+∠3+∠4=360
∠1=90
∠2=90
∠3=45
∠4=135
∠3 and ∠4 could be anything that adds up to 180
400
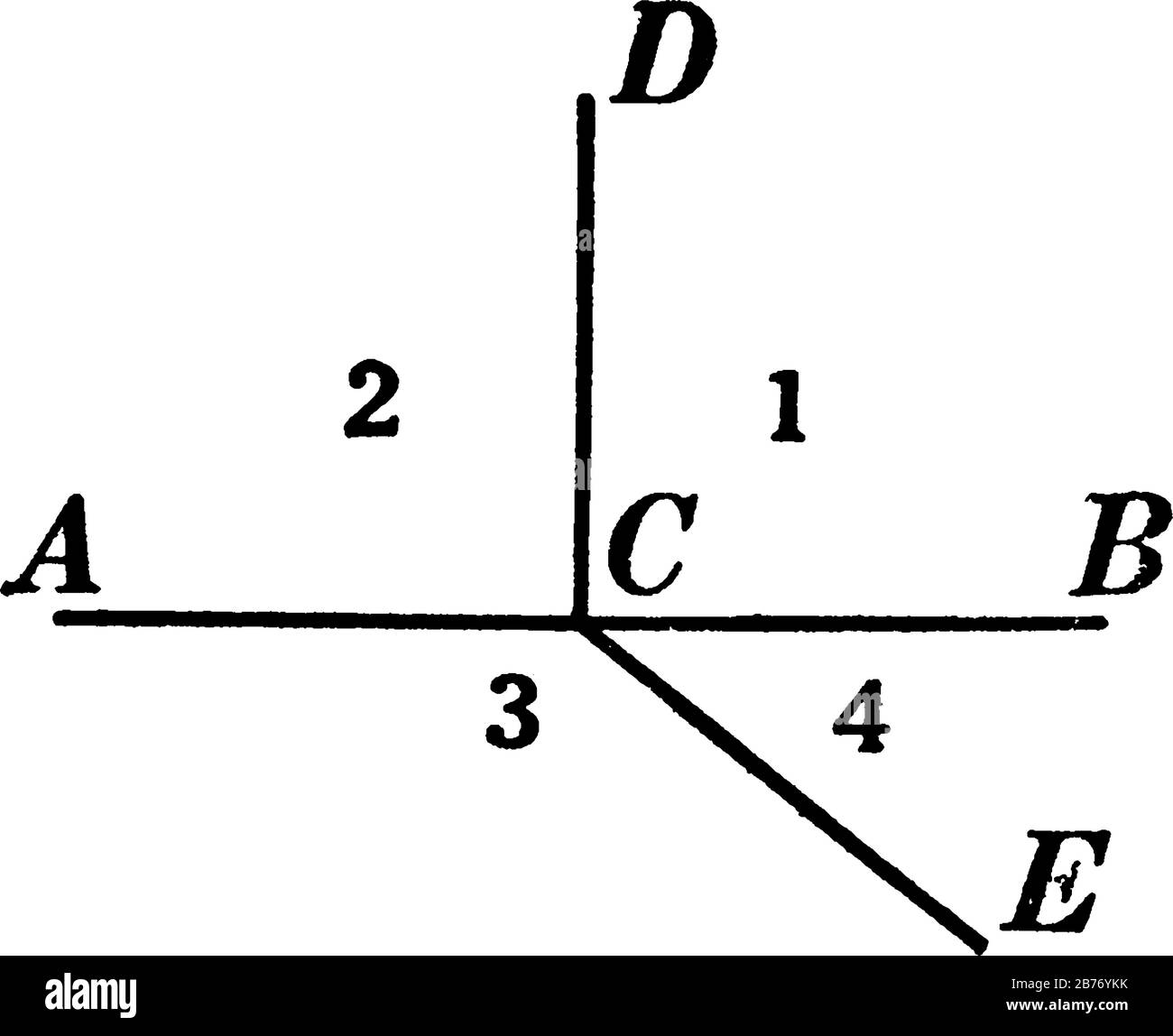
Fill in the missing condition
________IFF the rays coordinate is between the two others' coordinates
A ray is between two others in the same half rotation
400
What is a corollary to the ruler postulate?
Every line has a midpoint.
400
If angle A and angle B are complements and angle C and angle D are complements, what is the sum of all four angles?
180 degrees
∠A+∠B = 90
∠C+∠D=90
∠A+∠B+∠C+∠D=90+90=180
400
What is the value of each angle?
(2x-30)+(x+60)=180
3x=150
x=50
2x-30=2(50)-30=100-30=70
(50)+60=110
70,110
400
Fill in the Why?'s
Given: ∠1 and ∠2 are complementary and PB-PC-PD
Prove: AB⊥PD
1.
∠1 and ∠2 are complementary. Why?
2.
∠1 + ∠2 = 90 Why?
3. PB-PC-PD Why?
4. ∠BPD = ∠1 + ∠2 Why?
5. ∠BPD = 90 Why?
6. ∠BPD is a right angle Why?
7. AB⊥PD Why?
1. Given
2. Complementary angles add to 90
3. Given
4. Betweenness theorem
5. Substitution
6. Right angles equal 90 degrees
7. If a line forms a 90 degree angle with another line then they are perpendicular
500
Fill in the missing reasons for the proof
500
An angle is bisected twice, and then 15 degrees is added to it to get a right angle. What is the original angle?
90 - 15 = 75
2*75 = 150
150*2 = 300 deg
300 degrees is the original angle
500
On an analog clock, what are two times that make an angle that is the supplement of the angle of the time 3 O'clock? (assume that the hour hand stays on the hour hand for the whole hour)
9:00
6:15
3:30
9:30
10:05
8:25
there are many more, they just need to form a right angle.
500
What are the values of x and y?
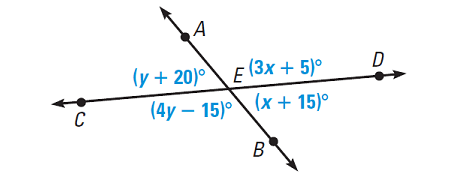
Many ways to do this
(3x+5)+(x+15)=180
4x=160
x=40
(3y+20)+(4y-15)=180
7y=175
y=25
500
Prove that Vertical Angles are equal
Given: ∠1 and ∠3 are vertical angles
Prove ∠1=∠3
Proof
1. ∠1 and ∠3 are vertical angles given
2. The sides to ∠1 are vertical opposite rays to the sides of ∠3 Definition of vertical angles
3. ∠1 and ∠2 are a linear pair; ∠2 and ∠3 are a linear pair ∠1 and ∠2 share a common side and the other sides are oposite rays. Same for ∠3 and ∠4
4. ∠1 and ∠2 are supplementary;∠2 and ∠3 are supplementary angles in a linear pair are supplementary
5. ∠1=∠3 Supplements of the same angle are equal.