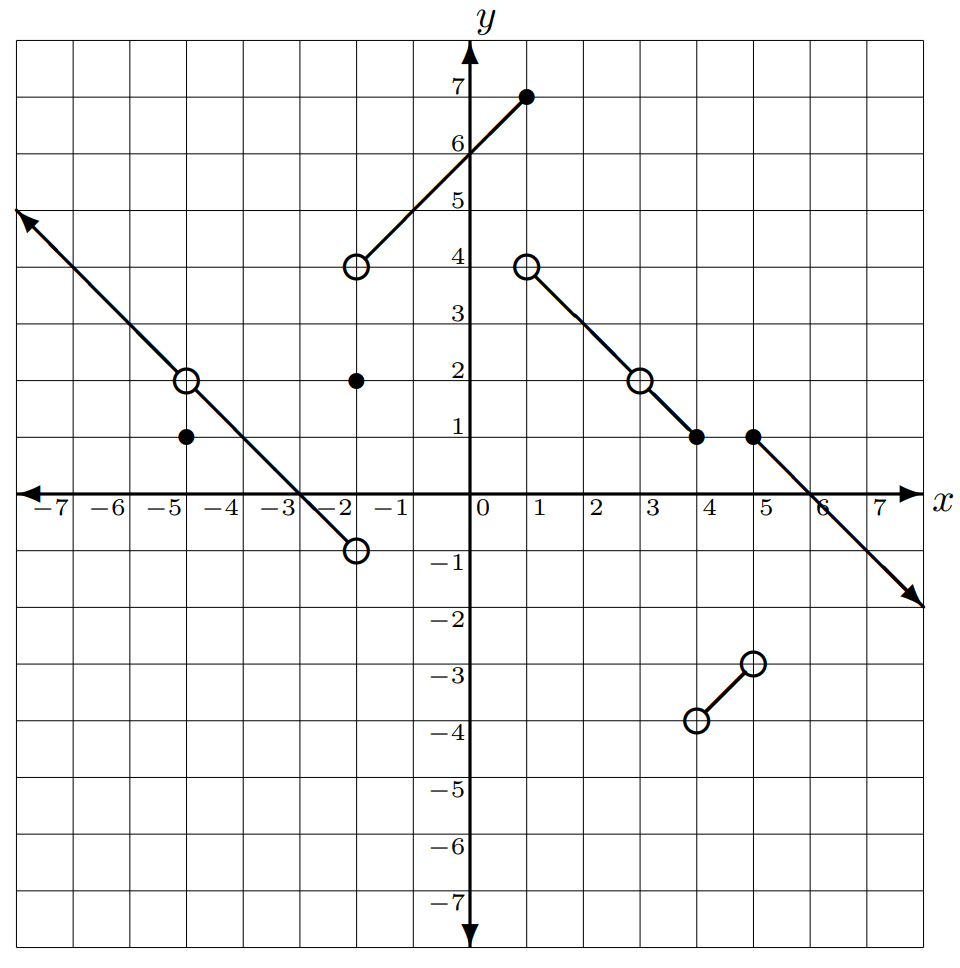
Estimate the limit by completing the following chart:
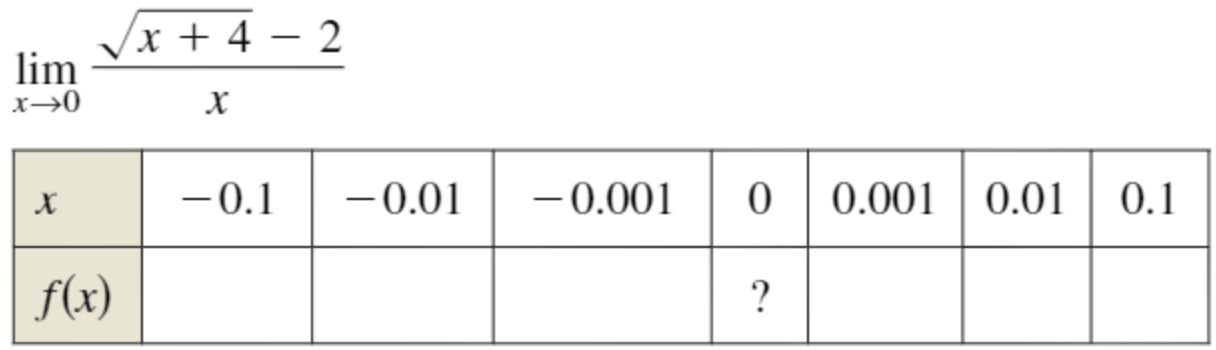
approx 0.25

Find:
lim_(x->0) (5x-3)
-3
Find:
lim_(x->5^-) f(x)
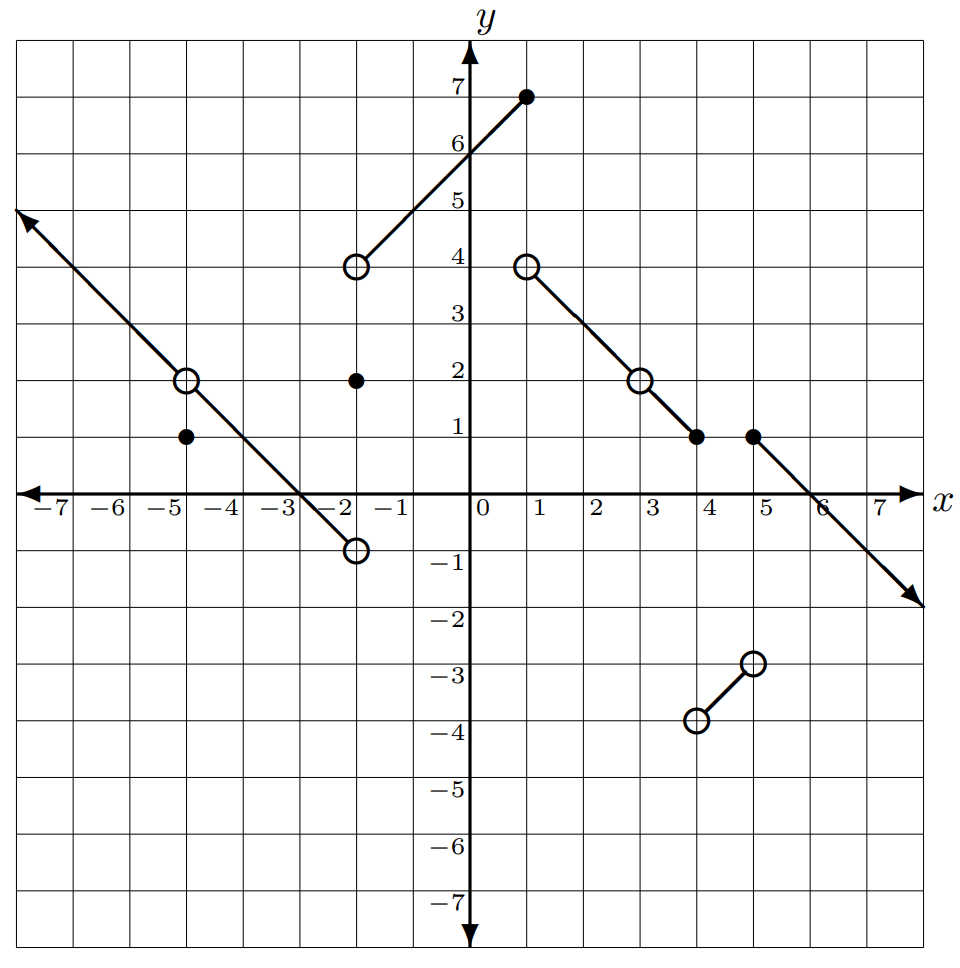
-3
Find:
lim_(x->(pi/2)^+) tan x
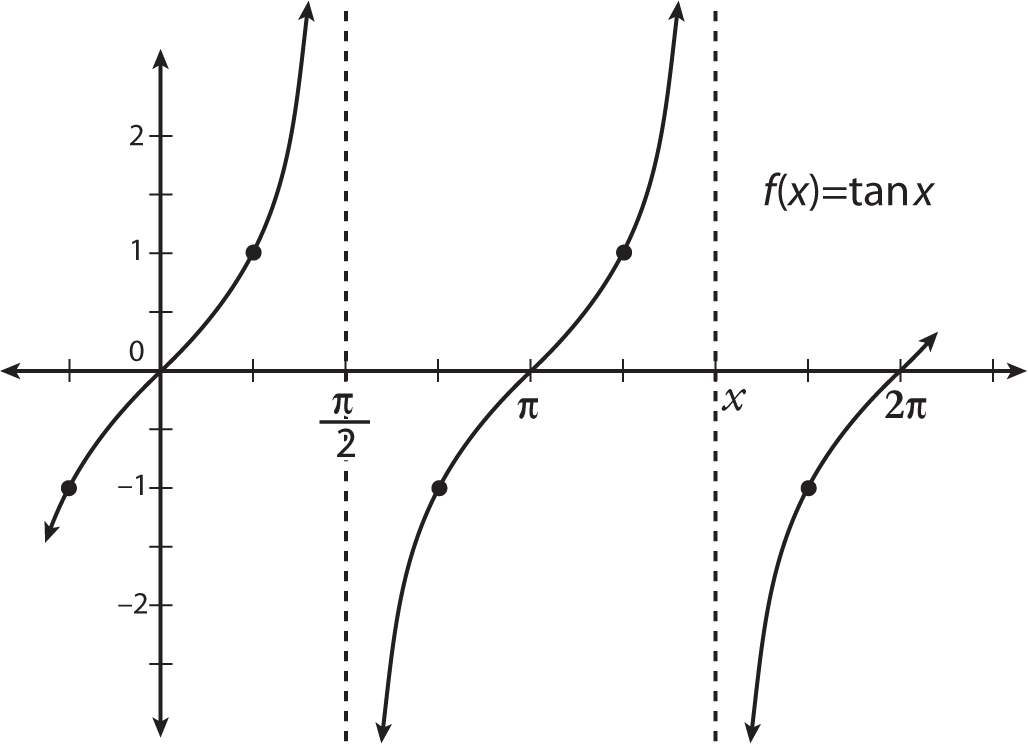
-oo
Draw and label a graph of f(x) where:
lim_(x->1) f(x) = DNE
*Answers will vary*
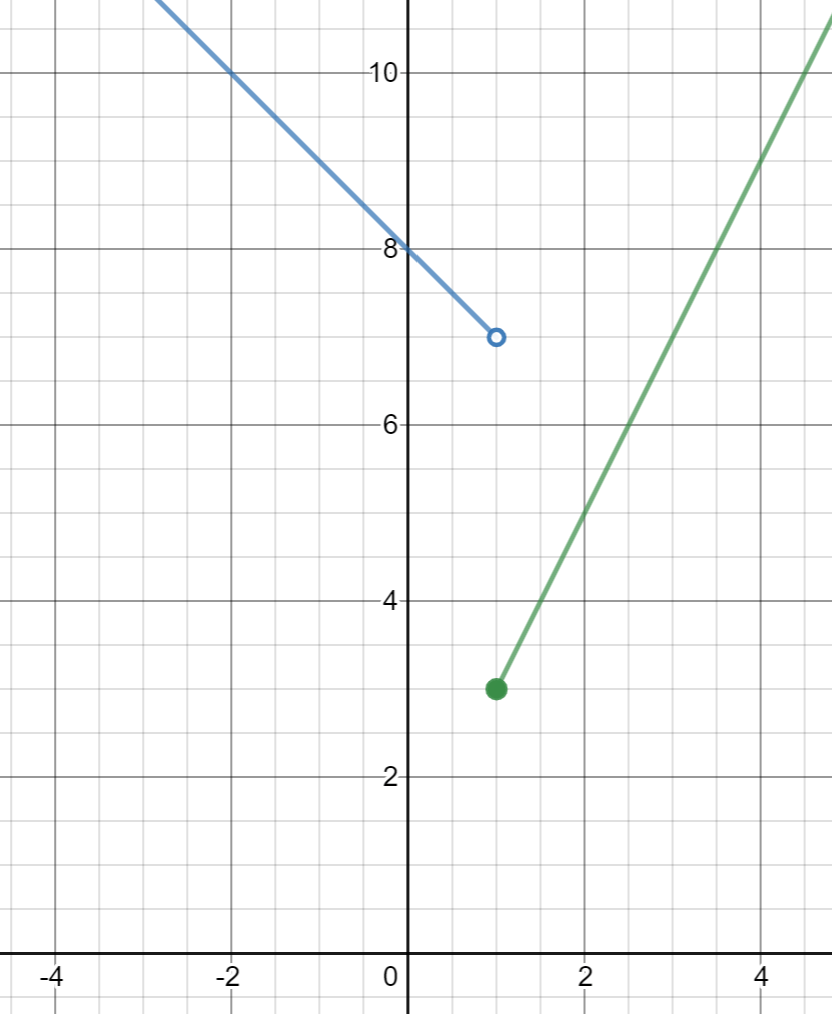
Find:
lim_(x->-5) f(x)

lim_(x->-5) f(x) = 2
Find:
lim_(x->4) (5)/(x-1)
5/3
Find:
lim_(x->6^+) (x-6)/(x^2-36)
1/12
Find:
lim_(x->4^-) (-1)/(x-4)
oo
Draw and label a graph of f(x) where:
lim_(x->-2^+) f(x) = oo
lim_(x->-2^-) f(x) = -oo
*Answers will vary*
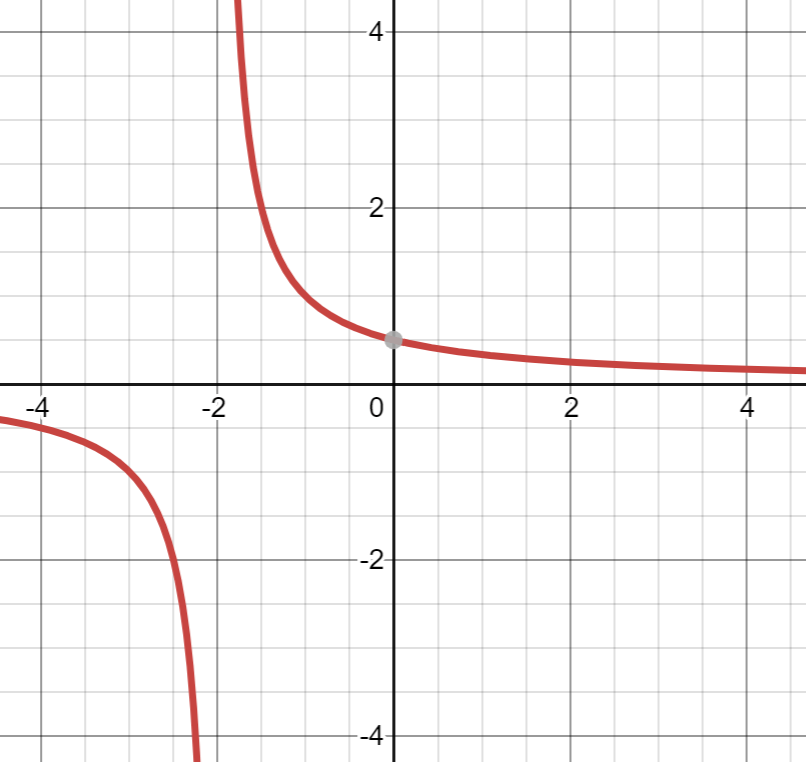
Find:
lim_(x->-2) f(x)

lim_(x->-2) f(x) = DNE, LS≠RS
Find:
lim_(x->4) (4-x)/((x^2)-16)
-1/8
Find:
lim_(x->4^-) (abs(x-4))/(x-4)
-1
Find:
lim_(x->4^+) (-1)/(x-4)
-oo
Draw and label a graph of f(x) where:
lim_(x->-2^-) f(x) = -0.5
lim_(x->-2^+) f(x) = 2
lim_(x->3) f(x) = DNE
*Answers will vary*
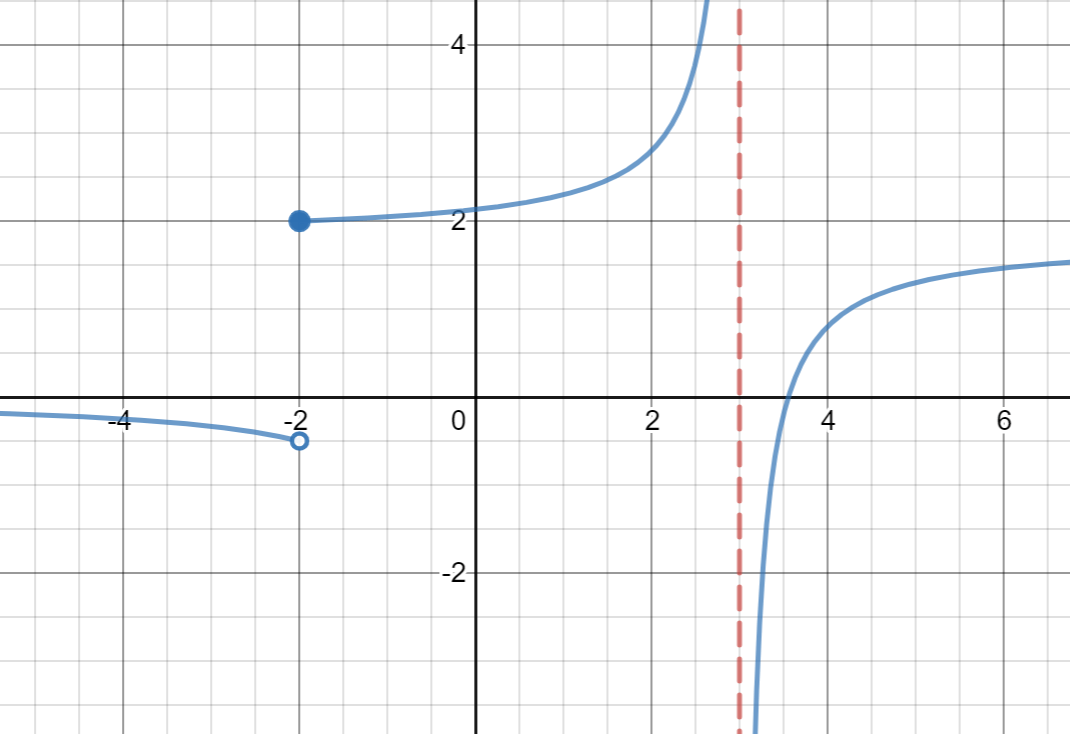
Find:
lim_(x->0) f(x)

lim_(x->0) f(x) = 6
Find:
lim_(x->0) (sqrt(4+x) - 2)/(x)
1/4
1. Find all x-values where f(x) is discontinuous.
2. State which x-values are removable and non-removable.
3. Write the intervals on which f(x) is continuous.
f(x) = (x^2-7x)/(3x^3-19x^2-14x)
1. x = -2/3, 0, 7
2. removable at x=0, x=7; non-removable at x=-2/3
3. x in (-oo, -2/3)U(-2/3,0)U(0,7)U(7,oo)
Find:
lim_(x->0^-) 1+1/x
-oo
Draw and label a graph of f(x) where:
f(2)=8; f(7)=-8
lim_(x->2^+)f(x)=6; lim_(x->2)f(x)=DNE; lim_(x->7)f(x)=-6
*Answers will vary*
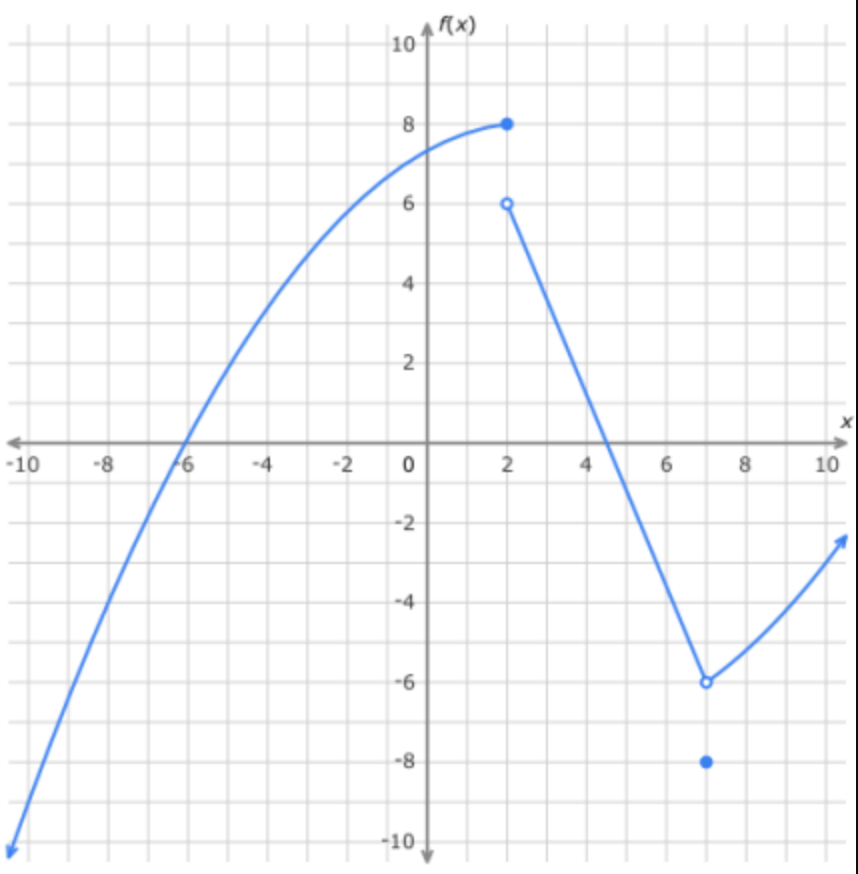
Find:
lim_(x->4) f(x)

lim_(x->4) f(x) = DNE, LS≠RS
Find:
lim_(x->0) (1/sqrt(1+x)-1)/x
-1/2
Find:
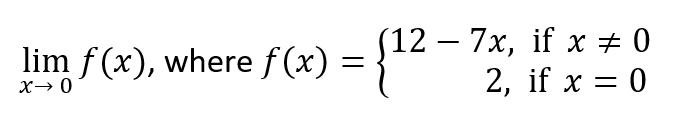
12
Find:
lim_(x->0^+) x+1/x+3
oo
Draw and label a graph of f(x) where:
f(-5)=1; f(-2)=2;f(1)=7;f(3)=undef.;
f(4)=f(5)=1;
lim_(x->-5)f(x)=2; lim_(x->-2)f(x)=DNE; lim_(x->4^+)f(x)=-4;
lim_(x->5^-)f(x)=-3
*Answers will vary*