1st Derivative Test (3.1-3.3)
2nd Derivative Test (3.4)
Limits at Infinity (3.5)
Curve Sketching (3.6)
Optimization Problems (3.7)
100
Find the all critical numbers from the first derivative of the function below:
y=x-sqrtx
x = 1/4
100
Find the all critical numbers from the second derivative of the function below:
y=x^3-9x^2
x=3
100
Find the limit, if it exists:
lim_(x->∞) 5
= 5
100
Find coordinates of all intercepts and equations of all asymptotes of the function given below:
f(x) = (2x)/(2x^2+x-1)
intercept: (0,0)
asymptotes: x = -1, x = 1/2, y = 0
100
Find the length and width of a rectangle that has a perimeter of 40 inches and has a maximum area.
10 inches by 10 inches
200
Find the coordinates of all relative extrema (max. and min.) using the first derivative test of the function below:
f(x)=(4x)/(x^2+1)
max: (1, 2)
min: (-1, -2)
200
Find the coordinates of all inflection points using the second derivative test of the function below:
f(x)=(x+9)^3
(-9, 0)
200
Find the limit, if it exists:
lim_(x->∞) 5x
= ∞
200
Find coordinates of all intercepts and equations of all asymptotes of the function given below:
f(x) = (sin(x))/(cos(x)), x ∈ [0, 2pi)
intercepts:
(0,0) and (pi, 0)
asymptotes:
x = pi/2, x = (3pi)/2
200
Find the length and width of a rectangle that has an area of 144 square meters and a minimum perimeter.
12 meters by 12 meters
300
Find the coordinates of all relative extrema (max. and min.) using the first derivative test of the function below:
f(x)=sin(x)+cos(x)
max: (pi/4,sqrt2)
min: ((5pi)/4,-sqrt2)
300
Find the coordinates of all inflection points using the second derivative test of the function below:
f(x)=x^2(4-x^2)
(-sqrt(2/3),20/9) and (sqrt(2/3),20/9)
300
Find the limit, if it exists:
lim_(x->∞) (1-4x)/(x+1)
= -4
300
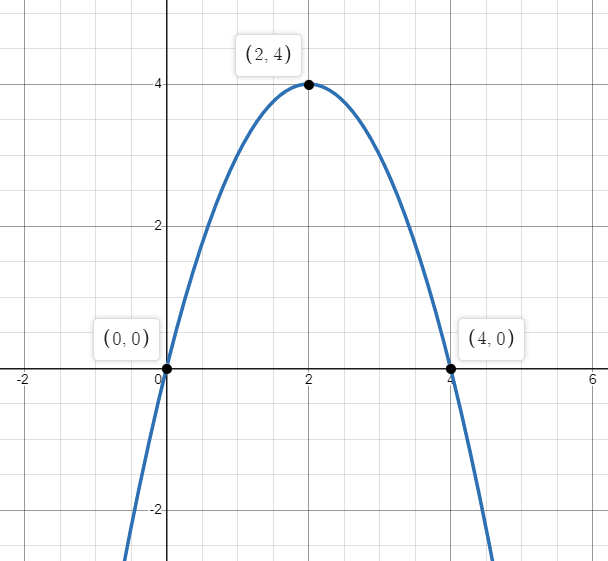
Analyze and sketch a graph of the function below using the first and second derivative tests. Label all intercepts, relative extrema, points of inflection, and asymptotes.
f(x) = 4x-x^2
intercepts: (0,0) and (4,0); rel. max: (2,4); no asymptotes, no points of inflection
300
A rectangular page is to contain 36 square inches of print. The margins on each side are to be 1.5 inches. Find the dimensions of the page such that the least amount of paper is used.
9 inches by 9 inches
400
Find the coordinates of all relative extrema (max. and min.) and the intervals of increasing/decreasing using the first derivative test of the function below:
f(x)=(x-2)(x+3)^2
max: (-3,0)
min: (1/3, -500/27)
↑: x ∈ (-∞, -3) U(1/3, ∞)
↓: x ∈ (-3, 1/3)
400
Find the coordinates of all inflection points and intervals of concavity (up/down) using the second derivative test of the function below:
f(x)=-2sin(x), x ∈ [0, 2pi)
(0,0) and (pi, 0)
conc.↑: x ∈ [0, pi)
conc.↓: x ∈ (pi, 2pi)
400
Find the limit, if it exists:
lim_(x->∞) (cos(x))/x
= 0
400
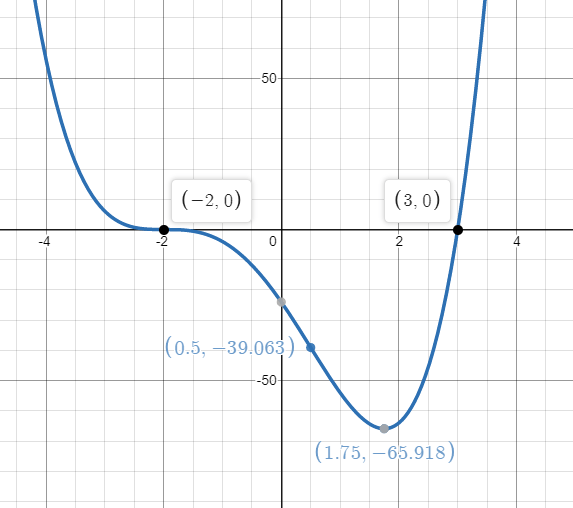
Analyze and sketch a graph of the function below using the first and second derivative tests. Label all intercepts, relative extrema, points of inflection, and asymptotes.
f(x) = (x-3)(x+2)^3
intercepts: (-2,0) and (3,0); rel. min: (7/4, -16875/256); points of inflection: (-2,0) and (1/2, -625/16); no asymptotes
400
Find the point on the graph of the function below that is closest to the point (6, 0).
f(x) = sqrt(x)
(11/2, sqrt(11/2))
500
Find the coordinates of all relative extrema (max. and min.) and the intervals of increasing/decreasing using the first derivative test of the function below:
f(x)=sin(x+pi)
max: ((3pi)/2,1)
min: (pi/2,-1)
↑: x ∈ (pi/2, (3pi)/2)
↓: x ∈ (0, pi/2) U((3pi)/2, 2pi)
500
Find the coordinates of all inflection points and intervals of concavity (up/down) using the second derivative test of the function below:
f(x)=x/(x+4)^2
(8, 1/18)
conc.↑: x ∈ (8, ∞)
conc.↓: x ∈ (-∞, -4)U(-4, 8)
500
Find the limit, if it exists:
lim_(x->-∞) (x)/sqrt(x^2+1)
= -1
500
Analyze and sketch a graph of the function below using the first and second derivative tests. Label all intercepts, relative extrema, points of inflection, and asymptotes.
f(x) = xsqrt(9-x^2), x∈[-3,3]
intercepts: (-3,0), (0,0), (3,0); inflection point: (0,0);
max: (sqrt(9/2),4.5); min:(-sqrt(9/2),-4.5)
500
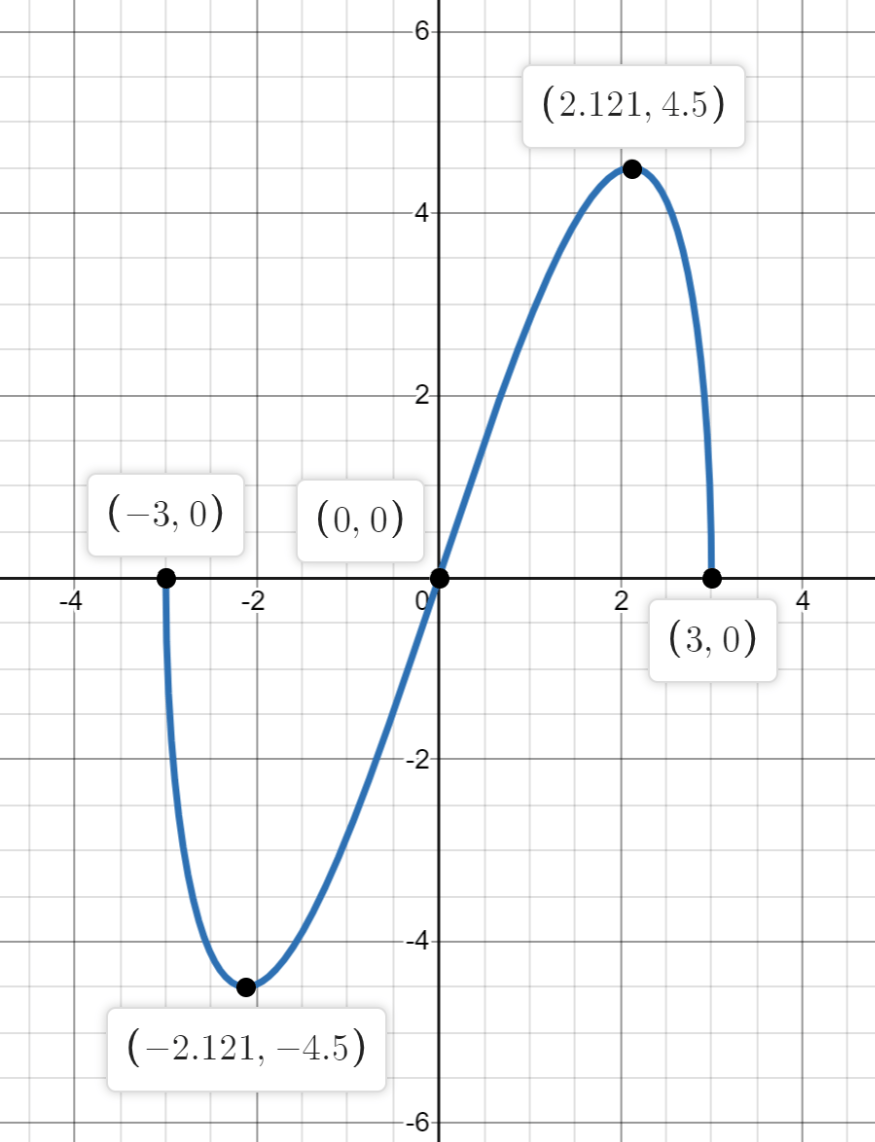
A right triangle in the first quadrant has the coordinate axes as sides, and the hypotenuse passes through the point (1, 8). Find the vertices of the triangle such that the length of the hypotenuse is minimum.
(0, 0), (5, 0), and (0, 10)