Parametric
Polar
Integration
Differential Equations
100
The velocity of a biker is defined as v(t) = (48y)/(3t+1) . Find the equation for acceleration.
a(t) = 48/(3t+1)^2
100
Convert the point (-1, pi) from polar coordinates to rectangular coordinates
(1,0)
100
Solve int ln x dx
xlnx - x + C
100
Let y=f(x) be the solution to the differential equation dy/dt = .45y with y(0) = 30
y = 30e^(.45t)
200
An object moving along the curve in the xy plane is at position <x(t), y(t)> at time t , where dx/dt = sin^-1(4-3e^-t) . The curve has a vertical tangent line at one point on the interval -1<t<0 . At what time is the object at this point?
ln 3/4
200
Convert the point (2, pi/3) from polar coordinates to rectangular coordinates
(1, sqrt(3))
200
Solve int x^2 e^-x dx
-x^2e^-x - 2xe^-x -2e^-x + C
200
Let y=f(x) be the solution to the differential equation y'=2x+y^2 with the initial condition f(1) = 3 . What is the approximate value of f(2) by using Euler's method with two steps of equal length starting at x=1 .
19
300
What is the velocity vector at time t=3 of the following set of parametric equations?
x=t^4-4t, y=2t^2+11t
<104, 23>
300
What is the slope of the line tangent to the polar equation r = cos theta when theta = pi/2 ?
0
300
Solve int x^2 cosx dx
x^2sinx + 2xcosx + 2sinx + C
300
Give the solution to dy/dt = 0.7y(1-y/4) with y(0)=3
y=4/(1+1/3(e^-0.7t))
400
If x=2t^2 and y = ln t , what is (d^2y)/dx^2 ?
-1/8t^4
400
Find the area inside the curve r=4costheta and outside the curve r=4sintheta in the first quadrant.
8
400
Solve int e^x sinx dx
(-e^xcosx + e^xsinx)/2 + C
400
Find the function y = f(x) which satisfies the differential equation dy/dx = 3x^2y with the initial condition that y(0) = 6 .
6e^(x^3)
500
Find the arclength of y=-x^2+9 from 0 <= x <= 3
9.747
500
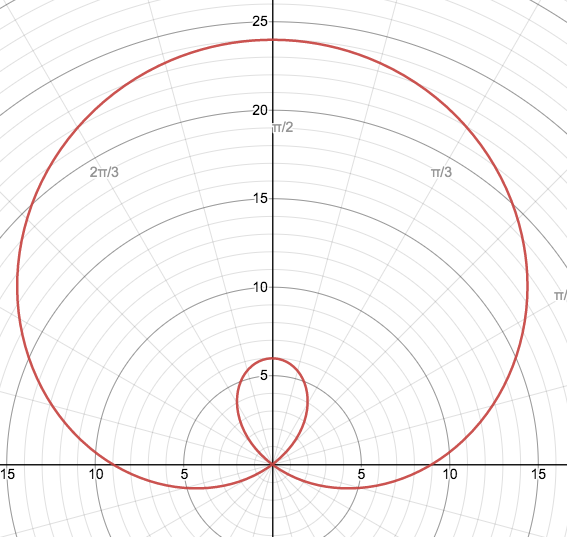
Find the area of the inner loop of the graph
r=9+15sin(theta)
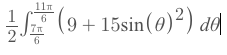= 20.526
500
Solve int (5x+7)/((x-1)(x+3))
3/(x-1) + 2/(x+3) + C
500
Find the function y=f(x) which satisfies the differential equation xy' + 2y' - 2 = 0 with the condition that f(5) = 0 .
y=2(ln|x+2|-ln|7|) or y=2(ln|(x-2)/7|