Trigonometry
Evaluate
Simplify
Graphing
Functions
100
The EXACT values of the six trigonometric functions of the angle: 2π / 3
100
log base 2 of 1/8
-3
100
-8x^-2
-8/x^2
100
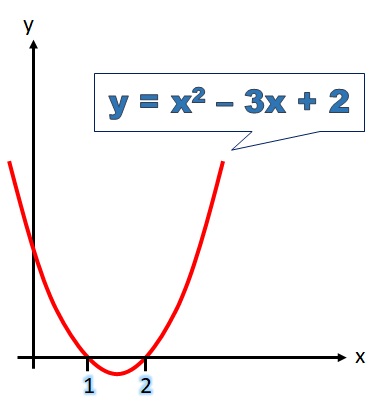
Graph y=x^2 - 3x +2 (label x and y intercepts)
100
State the domain of this function: (x^2 +2)/(2x^2 - 5x - 3)
R, x cannot equal -1/2, 3
200
Solve on [0, 2pi): sec x + 2 = 0
2pi/3, 4pi/3
200
ln e^7
7
200
(36x^10)^1/2
6x^5
200
State the vertical asymptotes of this function:
x / (x^2-3x+2)
x=2, x=1
200
Find the inverse of the following function:
y=x^3
y = (x)^1/3
f^-1 = x^1/3
300
Arcsec (2 rad(3)/3)
pi/6
300
sin pi
0
300
(27x^3)^-2/3
1 / 9x^2
300
State the horizontal asymptote of this function:
(3x^2)/(x^3 - 4x +3)
y=0
300
If f(x) = x^2 - x + 1 and g(x) = 2x - 1,
find f(g(-1))
f(g(-1)) = 13
400
Given theta is on the interval [0, 2π), find the EXACT value(s) of theta in radians, that makes the statement true: tan (theta) = rad(3)/3
pi/6 and 7pi/6
400
If f(x)= x^2 -5x +8, evaluate f(-6)
74
400
Factor completely: x^3 - x^2 +3x - 3
(x-1) (x^2 +3)
400
Consider the graph of the function f(x) = 4x - x^2. On which intervals is f(x) increasing and decreasing?
Increasing on (-infinity, 2)
Decreasing on (2, infinity)
400
f(-10) = 150
500
Solve for the EXACT values of x when x lies on [0,2pi]:
2cos^2 x+3cosx−2=0
pi/3, 5pi/3
500
If f(x)= x^2 -5x +8, evaluate f(x+h)
x^2 +2xh+h^2 - 5x - 5h +8
500
Factor completely: x^3 + 5x^2 - 4x - 20
(x+5)(x+2)(x-2)
500
See Image #2
C
500
A function is defined by the equation y = -3x - 4. If the domain is 1 <= x <= 5, what is the minimum value in the range of the function?
-19