The trig function that is defined as opposite over hypotenuse.
Sine
*Pass the marker to the next person*
What is the sine ratio given that theta is angle A?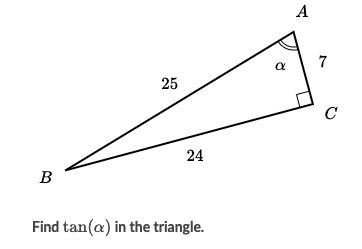
24/25
*Pass the marker to the next person*
The side opposite the right angle of a right triangle.
the hypotenuse
*Pass the marker to the next person*
The missing side of the right triangle when a=6 and c=10.
b=8
*Pass the marker to the next person*
The sun is 62 degrees above the horizon. A tree casts a shadow that is 12 feet long. How tall is the tree? (Round to the nearest tenth.)
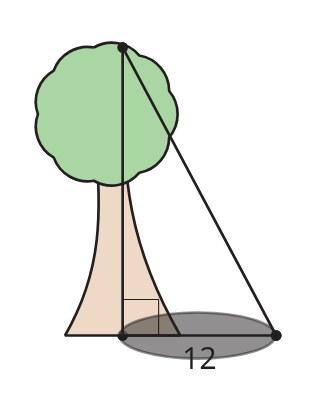
22.6 ft
(rounded)
*Pass the marker to the next person*
This trig function is defined as adjacent over hypotenuse.
cosine
*Pass the marker to the next person*
*DD*
What trig ratio do you need to use to solve for BC? What is the length of BC?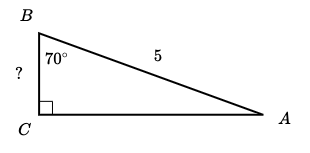
Cosine
BC = 1.71
*Pass the marker to the next person*
What is the only type of triangle you can use trig ratios with?
a right triangle
*Pass the marker to the next person*
The missing side of a right triangle when b=9 and c=15.
a=12
*Pass the marker to the next person*
A man flies a kite and lets out 100 feet of string. The angle of elevation of the string is 52 degrees . How high off the ground is the kite?
78.8 ft
*Pass the marker to the next person*
Determine tan(B)
15
8
*Pass the marker to the next person*
Solve for the measure of angle B. Round to the nearest degree.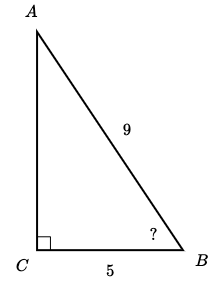
angle B = 56 degrees
*Pass the marker to the next person*
The formula needed when a third side length is missing from a right triangle and you have 2 other side lengths.
the Pythagorean Theorem
*Pass the marker to the next person*
Do the lengths 34, 25.5 & 44.7 create a triangle? If so, is it a right triangle?
Yes, they make a triangle.
No, it is not a right triangle.
(Doesn't fit the Pythagorean Theorem)
*Pass the marker to the next person*
The sun shines on a flagpole, causing a shadow to be cast on the ground. The distance from the base of the pole to the tip of the shadow is 49 feet. At that time of day, the sun’s rays make an angle of 38 degrees with the ground. How tall is the flagpole?
38.3 ft
*Pass the marker to the next person*
Use this trig function when you do not have the hypotenuse but you have the other two sides.
Tangent
*Pass the marker to the next person*
What is the value of x? Round to the nearest tenth.

x=43.8
*Pass the marker to the next person*
The 2 leftover acute angles in a right triangle total ____ degrees.
90
*Pass the marker to the next person*
Solve y. (Answers in reduced radical form.)
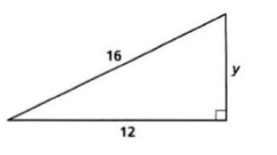
4root2 7
or
10.58
*Pass the marker to the next person*
a 10 foot ladder is leaning up against a wall. The base of the ladder is 4 feet from the wall. Find the angle of elevation the ladder makes with the ground. (Round to the nearest whole degree.)
66 degrees
*Pass the marker to the next person*
This is the function used when you want to know the angle, but are given two of the legs of the right triangle.
Inverse Tangent
*Pass the marker to the next person*
Find the missing angle measure, denoted with the question mark. Round to the nearest degree.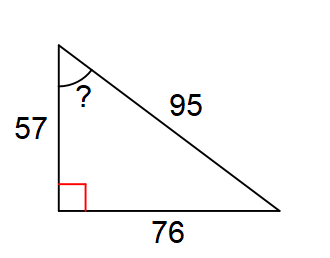
53 degrees
*Pass the marker to the next person*
Find the missing side length.
(Challenge: in reduced radical form)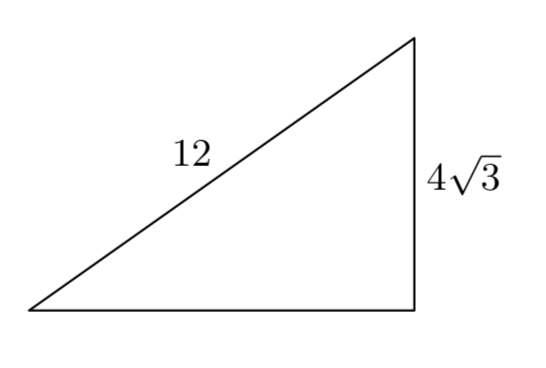
4root2 6
or
9.8
*Pass the marker to the next person*
A student whose eye level is 5 feet off the ground is staring at the roof of her school. the angle of elevation from her eye to the roof is 63 degrees. She is standing 10 feet from her school. How tall is the school?
(Round to the nearest tenth.)
24.6 ft
*Pass the marker to the next person*
