Line Integrals
Surface Integrals
Miscellaneous
Use the Theorem
Board Game Trivia
100
Evaluate the line integral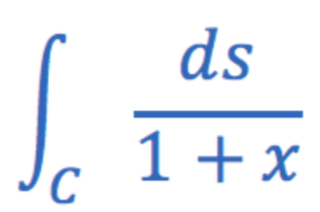 
Along curve C:
r(t)=<t,2/3t^(3/2)>, 0≤t≤1
2sqrt2-2
100
Find the mass of the surface 2x+3y+6z=12 in the first octant if the density at any given point is rho(x,y,z)=x^2+y^2
364/3
100
Write the equation of the surface
x^2+y^2-z^2=3
in parametric form
r(u,v)=<u,v,+-sqrt(u^2+v^2-3>
or
r(u,v)=<u,+-sqrt(3-u^2+v^2),v>
or
r(u,v)=<+-sqrt(3-u^2+v^2),u,v>
100
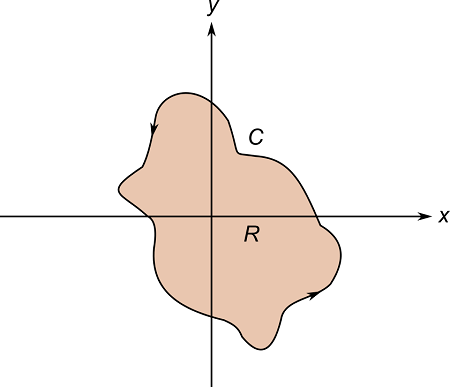
Evaluate the line integral
∫_C(y^3dx+3xy^2dy)
where C is the path shown below
0
100
In Scrabble, which letter is worth 5 points?
K
200
Find the mass of a wire that follows the curve:
r(t)=<e^tcost,e^tsint>, 0≤t≤1
if the density of the wire at any point is proportional to the distance between that point and the origin. (Assume k = 1).
(e^2-1)/sqrt2
200
Evaluate ∫∫_S(xy)dS if S is the surface defined as r(u,v)=<2cosu, 2sinu, v>, 0≤u≤π/2, 0≤v≤2
8
200
Write the equation of a cylinder with a radius of 2 centered around the z-axis in parametric form
r(u,v)=<2cosu, 2sinu, v>
or
r(u,v)=<u,+-sqrt(4-u^2),v>
or
r(u,v)=<+-sqrt(4-u^2),u,v>
200
Find the work required to move a particle from point (1, 1, 0) to point (0, 2, 3) through the vector field
F(x,y,z)=<2xy,x^2+z^2,2yz>
17
200
How many squares are on a traditional Scrabble board?
225
300
Find the work done by the force field
F(x,y)=<1/(x^2+y^2), 4/(x^2+y^2)>
on a particle that moves along the curve
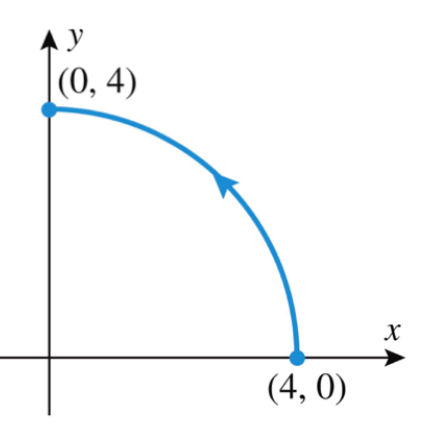
3/4
300
Evaluate ∫∫_S(z+3y-x^2)dS
where S is the portion of
z=2-3y+x^2
that lies over the triangle in the xy-plane with vertices (0,0), (2,0) and (2, -4)
1/3(26^(3/2)-10^(3/2))
300
Find a potential function for the vector field
F=<3y^2+2z, 6xy, 2x+e^z>
f(x,y,z) = 3xy2 + 2xz + ez + C
300
Use Stoke's Theorem to evaluate
∫∫_S(curlF•n) dS
if
F(x,y,z)=<ze^y,xcosy,xzsiny>
and S is the hemisphere
x^2+y^2+z^2=16, y≥0
oriented in the direction of the positive y-axis
16π
300
The properties in traditional Monopoly are based on what US city?
Atlantic City, NJ
400
Calculate the work required to move an object from point (1, 0, -2) to point (4, 6, 3) through vector field
F(x,y,z)=<yz, xz, xy+2z>
77
400
Calculate the flux of F=<3x, 2z, 1-y^2> over the surface with the equation z=2-3y+x^2 that lies over the triangle in the xy-plane with vertices (0, 0), (2, 0) and (2, -4) oriented in the positive z direction
412/3
400
Find the curl of the vector field
F = < 3x2, z3, 2yz >
< -x2, 0, 0 >
400
Use the divergence theorem to find the total flux flowing out of the closed cylinder x2 + y2 = 16 capped by the planes z=0 and z=5 for the vector field
F=<2x+3yz-z^2,3xz-3y+z^3,x^5y^4+2z>
80π
400
In the 1960s, Art Linkletter appeared on the $100,000 bills of what board game?
Life (or The Game of Life)
500
Evaluate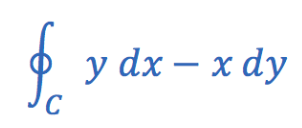 
along the curve pictured below
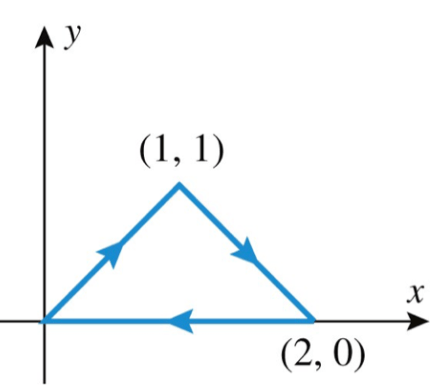
2
500
Use a surface integral to calculate the flux of the vector field F=<1,z,6x> through the portion of the sphere in the 2nd octant with a radius of 3 centered at the origin oriented outward.
-9/4π-45
500
Write the equation of the plane tangent to the surface with the equation
r(u,v)=<2ucosv,3usinv,u^2>
at the point (0, 6, 4)
4y-3z=12
500
Use Stokes' Theorem to evaluate ∫_CF•dr if
F=<3yx^2+z^3, y^2, 4yx^2>
and C is the triangle with vertices (0, 0, 3), (0, 2, 0) and (4, 0, 0) with a counter-clockwise rotation.
-5
500
The phrase, "back to square one," originates from what ancient board game?
Snakes and ladders
(now called Chutes and Ladders)