List what types of solutions a system of two linear equations can produce
AND
Explain what they mean.
Unique solution- two lines meet at a single point of intersection
No solution- two parallel lines that never cross
Infinitely many solutions - two lines that exist on top of one another along the same path
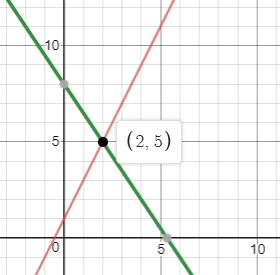
Solve the system below by graphing.
y=2x+1
3x+2y=16
Use the substitution method to solve the system below.
y=2x
6x+7y=20
(1,2)
Use the elimination method to solve the system below.
4x+8y=20
-4x+2y=-30
(7,-1)
The difference of two numbers is 3. Their sum is 13. Find the numbers.
5 and 8
Without solving, determine whether the system below has a unique solution, no solution, or IMS.
5x+2y=3
10x+4y=3
No solution
Find the equations of the lines below, then state their P.O.I.
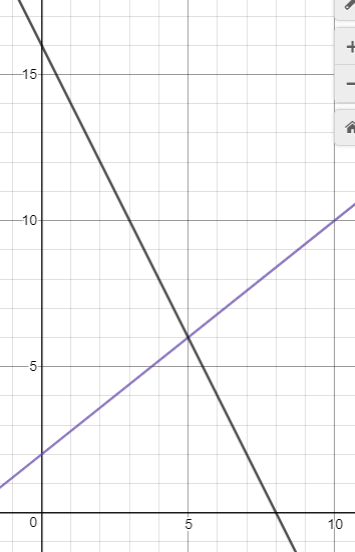
y=4/5x+2
y=-2x+16
(5,6)
Use the substitution method to solve the system below.
y-x=4
3x+6y=6
(-2,2)
Use the elimination method to solve the system below.
2x+8y=6
-5x-20y=-15
IMS
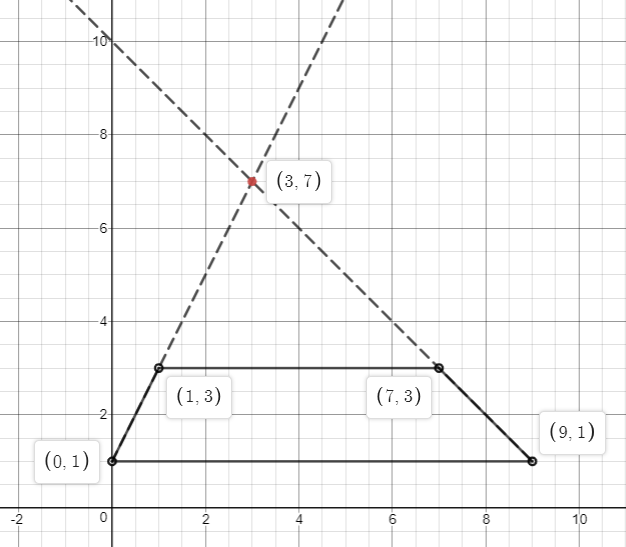
The points (1,3), (7,3), (0,1), and (9,1) are the vertices of a trapezoid.
Find the point of intersection of the lines on which lie the legs of the trapezoid.
The solution to the system below is IMS.
3x-2y=4
6x-4y=8
Give two points that are solutions to this system.
(0,-2)
(4/3,0)
(1, -1/2)
(2, 1)
Sketch three different graphs containing a system of equations with a unique solution, no solution, and IMS.
Show me your graphs
Use the substitution method to solve the system below.
x-y=7
5x=8+5y
No solution
Use the elimination method to solve the system below.
-x-7y=14
-4x-14y=28
(0,-2)
Matt and Ming are selling fruit for a school fundraiser. Customers can buy small boxes of oranges and large boxes of oranges. Matt sold 3 small boxes of oranges and 14 large boxes of oranges for a total of $203. Ming sold 11 small boxes of oranges and 11 large boxes of oranges for a total of $220. Find the cost each of one small box of oranges and one large box of oranges.
Small box of oranges: 7$
Large box of oranges: 13$