Functions
Graphing
Inverse
Combination of Functions
Domain and Range of Functions
100
Which sets of ordered pairs represent functions from A to B?
A={b, c, d, e} and B={16, 17, 18, 20}
a) {(b,16); (c,18); (d, 19); (c, 20) }
b) {(b,17); (c,17); (d, 18); (e, 20)}
c) {(c,18); (d,20); (e,16); (b,17)}
d) {(b,16); (c,17); (c,18); (e,20)}
b,c
100
Determine the open intervals on which the function is increasing, decreasing, or constant using interval notation. Put DNE if there is no answer.
Increasing: 
Decreasing: 
Constant: DNE
100
Can (1,6) and (1,7) be two ordered pairs of a one-to-one function?
No
100
Use the graphs of f and g to graph h(x) = (f + g)(x). (To graph h(x), use 4 segments each with closed end points on both ends.)
100
Given : f(x)= |x-4| , g(x)=3-x
Find the domain(in interval notation) of:
a) f
b) g
c) f(g)
a) (-∞,∞)
b) (-∞,∞)
c) (-∞,∞)
200
Determine whether each function is even, odd, or neither:
a)f(x)= x3 -5x
b) g(s)= 4s2/3
c) h(t)= t3 -1
a) odd
b) even
c)neither
200
Find the inverse of f(x)=√(7x-6)
y= (1/7)x2 +6/7
200
Find each of the following, if possible.
a) f(g)
b) g(f)
c)(f(g))(0)
a) f(g) = x
b) g(f) = x
c) (f(g)(0) = 0
200
Find the values of x for which f(x)=g(x) given:
f(x)= x2+2x+2 , g(x)= 7x-4
x= 3, 2
300
Find the difference quotient and simplify your answer:
f(x) =7x2 -2x+3
f(x+h)-f(x) / h, h≠0
14x+7h-2, h≠0
300
Find the domain and range of the inverse function of f(x)=|x-6| x ≥ 6
Inverse Function: f-1(x)=x+6
Domain: [0,∞)
Range: [6,∞)
300
Given f(x) = 4/(x2-1) , g(x)=x+1
Determine the domains of the following:
a) f
b) g
c) f(g)
a) 
b) 
c) 
400
A rectangle is bounded by the x-axis and the semicircle y =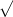 
36 − x2, as shown in the figure below.
a) Write the area A of the rectangle as a function of x.
b) Determine the domain of the area function. (Enter your answer for the domain using interval notation.)
a) A=2x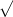36 − x2
b) [0,6]
400
Use the graphs of f and g to evaluate the functions.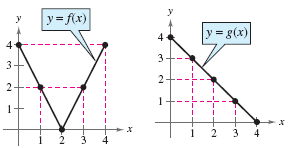
a) (f(g))(3)
b) (g(f))(2)
a) 2
b) 4