Average Rates of Change/Concavity
Transformations
Inverses
Mathematical Modeling
Compositions
Characteristics of Functions
100
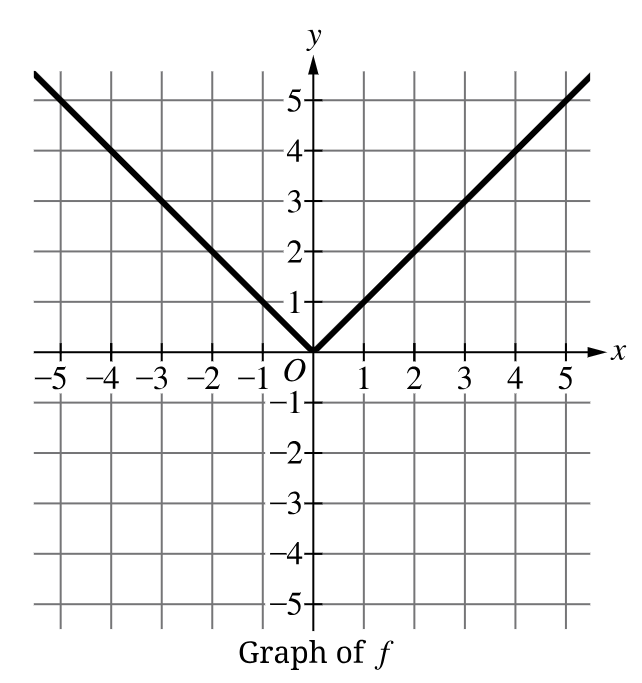
The graph of the function f is shown. What is the average rate of change of f on the interval -3<=x<=3 , if it exists?
What is "0"
100
Assume that a function f exists. If g is the function given by g(x)=2x , what graphical transformation is being applied for the composite function y=f(g(x)) ?
What is "horizontal dilation by a factor of
1/2"
100
The function f is given by f(x)=x+2 . If f^(-1)(n)=4 , what is the value of n ?
What is "6"
100
The rate of change R of the temperature of an object is proportional to the difference between the temperature T of the object and the temperature T_e of the environment in which the object is placed.
What is
R=k(T-T_e)
100
Using f(x)=6x^2 and g(x)=14x+4 , determine
(g@f)(1)
What is
(g@f)(1)=88
100
Given that f(x)=x^3-5x^2+7x-5 , evaluate f(2) without a calculator!
What is
f(2)=-3
200
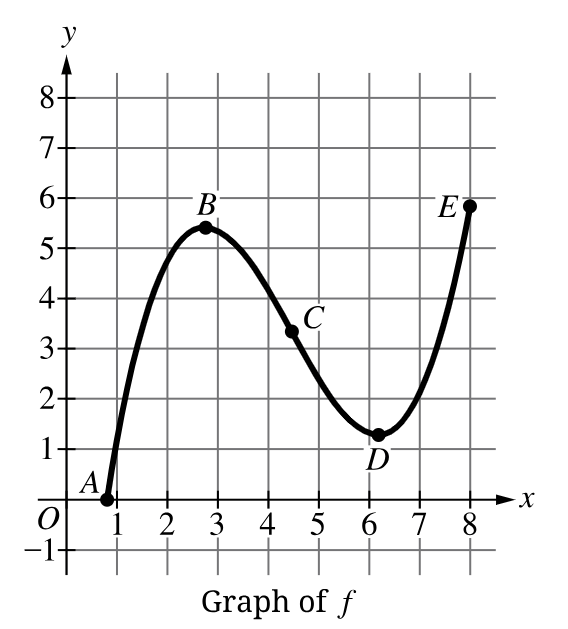The figure shows the graph of a function f . The zero and extrema for f are labeled, and the point of inflection of the graph of f is labeled. Let A, B, C, D, and E represent the x -coordinates at those points. On which interval is f increasing and the graph of f concave down?
What is "the interval from A to B "
200
Describe the sequence of transformations for h(x)=-(x+2)^2-3
What is "horizontal transformation of -2 units, reflection about the x-axis, and vertical transformation of -3 units"
200
Determine whether h(x)=(x-5)^2 has an inverse function an justify your answer.
What is "Given that h(x) fails the horizontal line test, h(x) is guaranteed to not have an inverse within its natural domain"
200
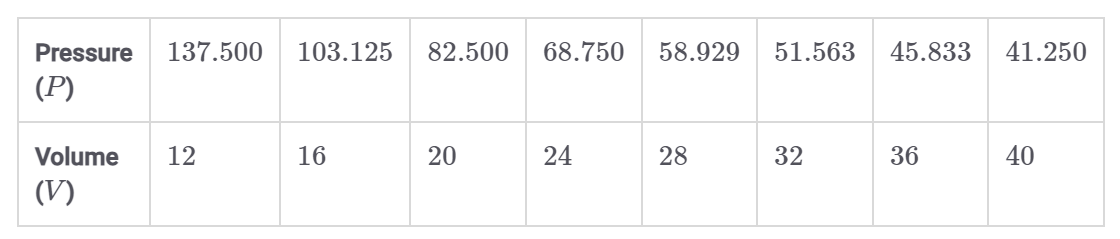Boyle's Law states that the pressure of a gas is inversely proportional to the volume of the gas at a constant temperature. The table gives the volume V , in milliliters (mL), of a gas for selected pressures P . What model will depict the volume of the gas as a function of pressure?
What is
V(P)=1650/P
200
A pebble is dropped into a calm pond, causing ripples in the form of concentric circles. The radius r (in feet) of the outer ripple is r(t)=0.6t , where t is the time in seconds after the pebble strikes the water. The area A of the circle is given by the function A(r)=pir^2 . Find and interpret (A@r)(t) .
What is
(A@r)(t)=0.36pit^2
This represents the area of the formed ripple after a period of time t, rather than the area formed by a current unknown radii
200
The function h is given by h(x)=-x^4+x^3+20x^2 . h(x) has a global maximum at which coordinate point?
What is
(3.559,137.97)
300
A linear function P is used to model the price, in dollars, of used cars as a function of their age t , in years. It is known that P(4)=7300 and P(7)=5500 . Based on this model, for each year that a car ages, its price decreases by approximately what amount?
What is "
$600"
300
For the function f , it is known that f(3)=0 and f(6)=-4 . The function g is given by g(x)=f(x-4) . What is the solution to g(x)=0 ?
What is
x=7
300
Determine the inverse of f(x)=3x^3+8 and state its respective domain and range.
What is
f^-1(x)=root(3)((x-8)/3
Domain:
{x|x in RR}
Range:
{y|yinRR}
300
A model rocket is launched from a site on level ground. One second after the rocket is launched, it is at a height of 20.1 meters above the ground. One additional second later, it is at a height of 30.4 meters above the ground. A quadratic regression using the heights of the rocket at times t=0,t=1, and t=2 seconds is calculated to model the rocket's height above the ground, in meters, at time t seconds. At what time t seconds, does the model predict that the rocket will land back on the ground?
What is
t=5.102
300
Given f(x)=15sqrtx and h(x)=9/x^2 , find the domain of (h@g)(x) .
What is:
Domain:
x in (0,oo)
300
Find the x - and y-intercepts of the function f(x)=x^2+8x-9 .
What is
x-intercepts:
(-9,0) and (1,0)
y-intercept:
(0,-9)
400
The rate of people entering a subway car on a particular day is modeled by the function R , where R(t)=0.03t^3-0.846t^2+6.578t+1.428 for 0<=t<=20 . R(t) is measured in people per hour, and t is measured in hours since the subway began service for the day. Based on the model, at what value of t does the rate of people entering the subway car change from increasing to decreasing?
What is
t=5.505
400
The numbers N (in thousands) of married couples with stay-at-home mothers from 2000 through 2007 can be approximated by the function N=-24.70(t-5.99)^2+5617, 0<=t<=7 where t represents the year, with t=0 corresponding to 2000.
Describe the transformation of the parent function and use the model to predict the number of married couples with stay-at-home mothers in 2015.
What is "The parent function has a horizontal transformation of 5.99 units, vertical dilation by a factor of 24.70, reflected about the x-axis, and a vertical shift of 5617 units. At the year 2015, it is predicted that there will be an approximation of 3,611.851 thousands of stay-at-home mothers"
400
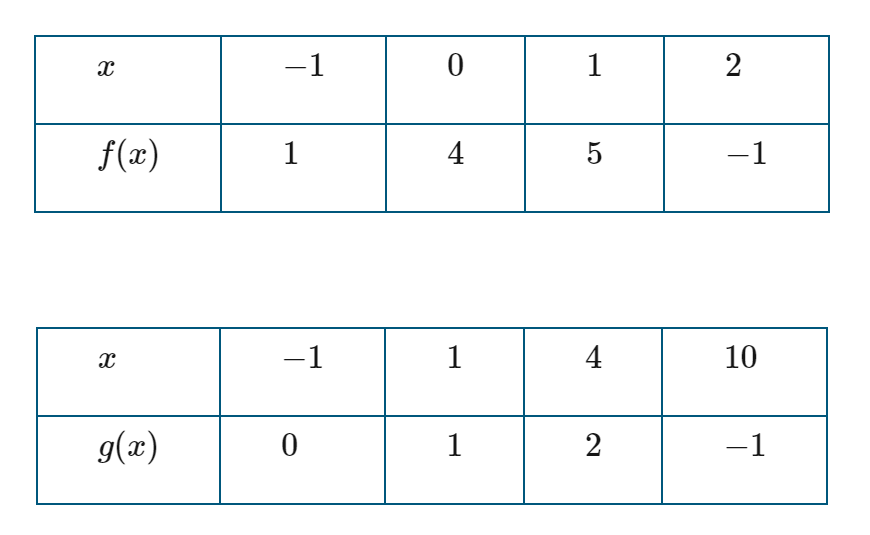The tables give values of the functions f and g for selected values of x . What is the value of g^(-1)(f(2)) ?
What is "10"
400
A stream with a velocity of 1/4 mile per hour can move coarse sand particles about 0.02 inch in diameter. Approximate the velocity required to carry particles 0.12 inch in diameter.
What is
.612 (mi)/(hr)
400
Given that values of f and g are given through the provided table, evaluate (f@f)(3) .
What is
(f@f)(3)=7
400
Given that f(x)=x^3-6x^2+9x+1 , determine whether there is an instance in which f(x)=6 . Justify your answer (IVT).
What is "Given that f(x) is a continuous function for all x within [4,5], and f(4)=5 and f(5)=21, the IVT guarantees at least one instance in which f(x)=6 within the x interval [4,5]
500
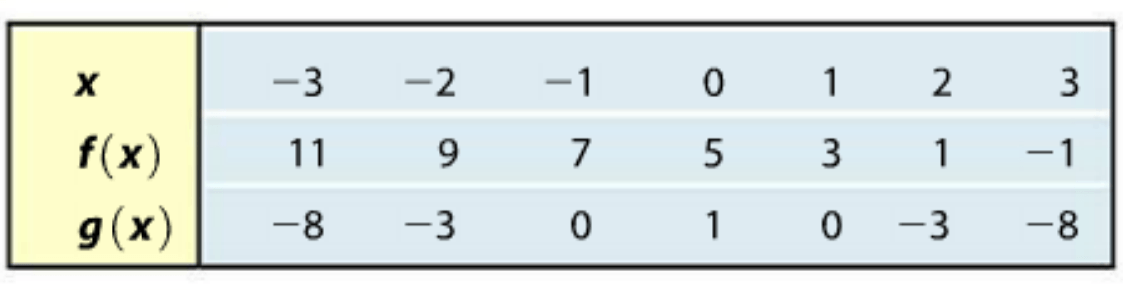
The graph depicts a function that resembles the rate of change of an original given function f . Determine the intervals of concavity and the points of inflection for the original given function f .
What is
Concave Up:
x in (-oo,-4)uu(1,5)
Concave Down:
x in (-4,1)uu(5,oo)
Points of Inflection:
x=-4, x=1, and x=5
500
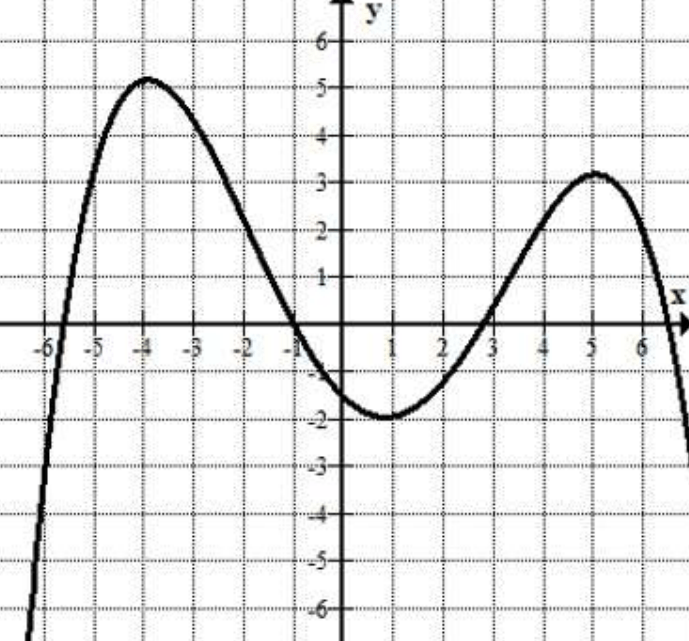
Graph the following function (label your original and transformed key points):
f(x)=-3(-2x+2)^3+1
What is 
500
Given that f(x)=x^2+x-1 and g(x)=5x^2-8x-1 , what is (f^-1@g)(0) ?
What is
(f^-1@g)(0)=0
500
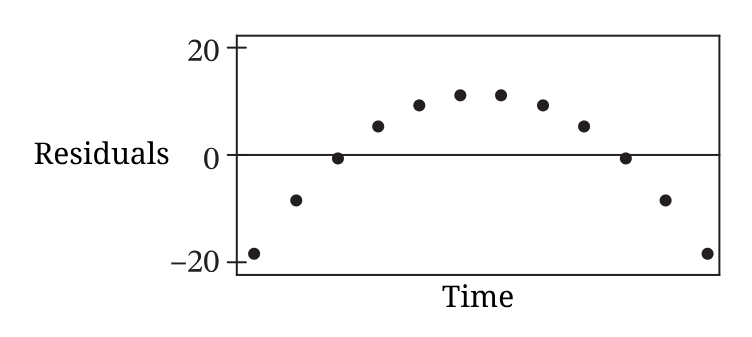A food vendor developed a new sandwich type for sale. The vendor made estimates about the sales of the new sandwich type over time. A linear regression was used to develop a model for the sales over time. The figure shows a graph of the residuals of the linear regression. Is a linear model appropriate or not appropriate to estimate their future sales and justify your reasoning.
What is "The linear model is not appropriate because there is a clear pattern in the graph of the residuals"
500
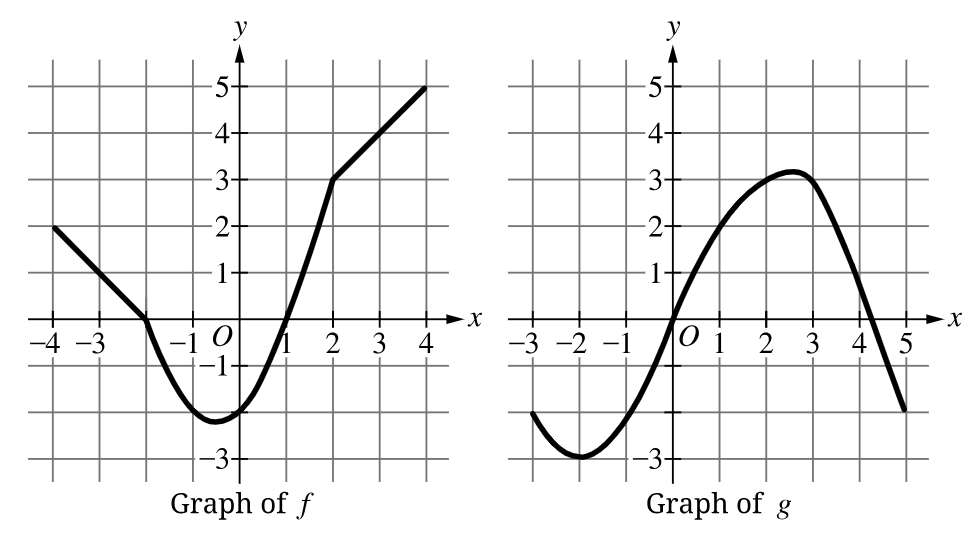The graphs of y=f(x) and y=g(x) are given. What is the value of f(f(g(1))) ?
What is "4"
500
Approximate the intervals in which the function g(x)=x^4-2x^2-3 is increasing and decreasing. (Calculator)
Increasing Intervals:
x in (- oo,-1)uu(0,1)
Decreasing Intervals:
x in (-1,0)uu(1,oo)