Chapter 2: Transformations Jeopardy Template

Vocabulary

Reflections

Rotations

Two or More Transformations

Dilations

Surprise

100

Also called a 'flip'. What kind of motion is this transformation?

(You should have two answers)

A flip is referred as a Reflection and it is a Rigid motion.

100

Draw the figure and its reflection in the x-axis. Identify the coordinates of the image.

𝐾 (3,3), 𝐿 (2,1), 𝑀 (1,2), 𝑁 (2,5)

K′(−3, −3), L′(−2, −1), M′(1, −2), N′(2, −5)

100

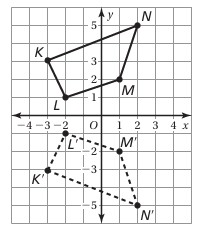
Tell whether the dashed figure is a rotation of the solid figure about the origin. If so, give the angle and direction of rotation.

yes; 90° counterclockwise

100

The vertices of a rectangle are 𝐴(1,1), 𝐵(1,1), 𝐶(1,2), and 𝐷(1,2). What are the coordinates of the image after dilating the rectangle using a scale factor of 3, and then translating it 2 units right and 1 unit up?

A'(-1,4), B'(5,4), C'(5,5), D'(-1,5

100

The vertices of a figure are given. Draw the figure and its image after a dilation with the given scale factor. Identify the type of dilation.

𝐴(3,−1), 𝐵(−4,4), 𝐶(−2,−3); k = 5

Enlargement

100

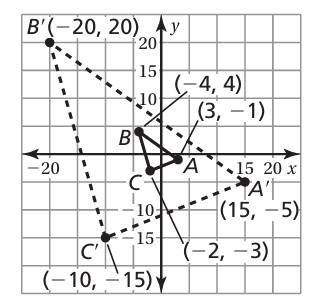
You rotate a triangle 270° counterclockwise about the origin. Then you translate its image 2 units right and 1 unit down. The vertices of the final image are (0,2), (8,−1), and (5,−2). What are the vertices of the original triangle?

(−3, −2), (0, 6), (1, 3)

200

Also called a turn. What kind of motion is this?

(You should have two answers)

A turn is referred as a Rotation and it is a rigid motion.

200

Draw the figure and its reflection in the x-axis. Identify the coordinates of the image.

𝑂 (2, 1), 𝑃 (1, 3), 𝑄 (1, 4), 𝑅 (3, 1)

O′(−2, 1), P′(−1, 3), Q′(1, 4), R′(3, 1)

200

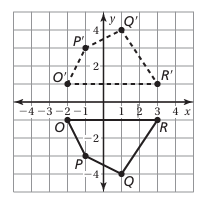
The vertices of a trapezoid are 𝑨(𝟏,𝟏), 𝑩(𝟐,𝟐), 𝑪(𝟒,𝟐), and 𝑫(𝟓,𝟏). Rotate the trapezoid 90° clockwise about the origin. Find the coordinates of the image.

A′(1, −1), B′(2, −2), C′(2, −4), D′(1, −5)

200

Translate the figure, A(0,3), B(1,0), C(1,1), 3 units to the left and Dilatite Image ABC by 2.

A''(-6,6), B''(-4, 0), C''(-2,1)

200

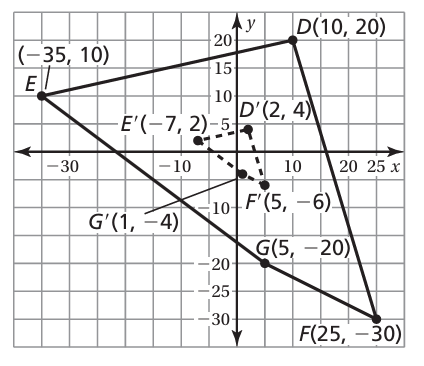
The vertices of a figure are given. Draw the figure and its image after a dilation with the given scale factor. Identify the type of dilation.

𝐷(10,20), 𝐸(−35,10), 𝐹(25,−30), 𝐺(5,−20); 𝑘= 1/5

Reduction

200

If I have a rectangular yard with a length of 15.6 yards, and a width of 16.6 yards. What would be my scale factor if I want to increase the lengthto 39 and the width to 41.5? Explain your answer.

Scale Factor of 2.5

300

Also called a 'slide'. What kind of motion is this?

(You should have two answers)

A slide is referred to as a translation and it is a rigid motion.

300

Draw the figure and its reflection in the y-axis. Identify the coordinates of the image.

𝐵 (2, 3), 𝐶 (3,1), 𝐷 (5,3), 𝐸 (3,0)

B′(− 2, −3), C′(−3, 1), D′(−5, 3), E′(−3, 0)

300

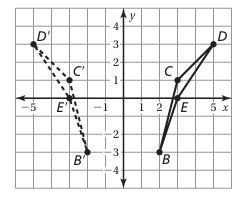
The vertices of a rectangle are F(–5, –1), G(–2, –1), H(–2, –3), and I(–5, –3). Rotate the rectangle 270° clockwise about the origin, and then reflect it in the y-axis. What are the coordinates of the image?

F'' (–1, –5), G'' (–1, –2), H'' (–3, –2), I'' (–3, –5)

300

The vertices of a trapezoid are 𝑨(𝟏,𝟏), 𝑩(𝟐,𝟐), 𝑪(𝟒,𝟐), and 𝑫(𝟓,𝟏). Rotate the trapezoid 270° counterclockwise about the origin. Find the coordinates of the image.

A′(1, −1), B′(2, −2), C′(2, −4), D′(1, −5)

300

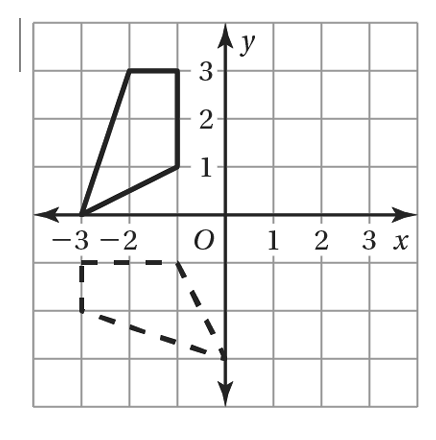
The dashed figure is a dilation of the solid figure. Identify the type of dilation and find the scale factor. Explain your reasoning.

(You should have two answers AND an explanation)

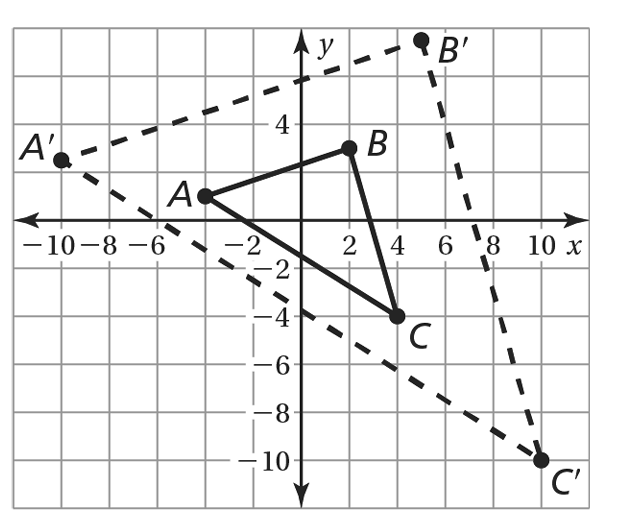
enlargement

k = 5/2

The coordinates of the vertices changed according to (x, y) -> ( 5/2 x , 5/2 y ) .

Since k > 1, it is an enlargement.

300

You have a triangle that has side lengths of 6, 9, and 12.

a. Give the side lengths of a similar triangle that is smaller than the given triangle. Justify your answer.

b. Give the side lengths of a similar triangle that is larger than the given triangle. Justify your answer.

400

Describe non-rigid motions and give an example of a non-rigid motion that we've explored in class.

(You should have two answers)

Non-rigid motions will change the shape and/or size of a figure; Dilations.

400

Draw the figure and its reflection in the y-axis. Identify the coordinates of the image.

𝐺 (5, 5), 𝐻 (3, 1), 𝐼 (2,4), 𝐽 (1, 1)

G′(5, −5), H′(3, −1), I′(2, 4), J′(1, −1)

400

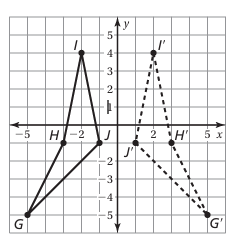
Tell whether the dashed figure is a rotation of the solid figure about the origin. If so, give the angle and direction of rotation. If not, explain what kind of transformation it is.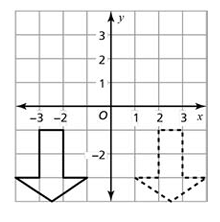

No. The figure is reflected over the y-axis.

400

The vertices of a quadrilateral are 𝑃(−6,6), 𝑄(−2,6), 𝑅(−3,2), and 𝑆(−6,2).

First, reflect PQRS over the y-axis. Then, translate 6 units left and 8 units down. Finally, rotate 90° counter-clockwise about the origin.

What are the coordinates of the image?

P'''(2,0),Q′′′(2,−4),

R′′′(6,−3), S′′′(6,0)

400

A triangle is dilated using a scale factor of 1/2. The image is then dilated using a scale factor of 1/3. What scale factor could you use to dilate the original triangle to get the final image?

1/6

400

The two parallelograms are similar. Find the degree measure of each angle.

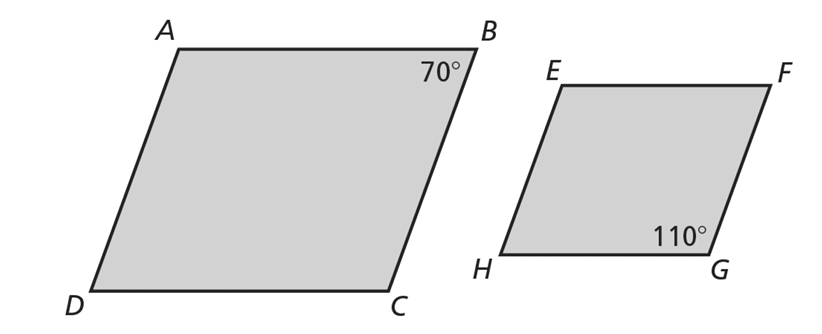
angle A=110^@

angle C=110^@

angle D=70^@

angle E=110^@

angle F=70^@

angle H=70^@

500

Describe in your own words the difference between similar figures and congruent figures. Create a sketch that represents both ideas.

(You should have two answers)

Similar = same shape, not necessarily same size. When one imagine is obtained using rigid AND/OR non-rigid motions. Congruent = same shape, same size. When one image is obtained using rigid motions ONLY.

500

DeltaABC has vertices 𝐴(2, 1), 𝐵(4,2), and 𝐶(2, 2).

Reflect DeltaABC over the x-axis, giving Delta𝐴′𝐵′𝐶′. Then reflect Delta𝐴′𝐵′𝐶′ over the y-axis.

What are the coordinates of the resulting triangle?

A″(2, 1), B″(−4, −2), C″(−2, 2)

500

The vertices of a triangle are A(–4, 1), B(–2, 2), and C(–1, 1). Rotate the triangle 180° about the origin. Find the coordinates of the image.

A′(4, –1), B′(2, –2), C′(1, –1)

500

The blue figure is a transformation of the red figure. Use coordinate notation to describe the transformation. Explain your reasoning

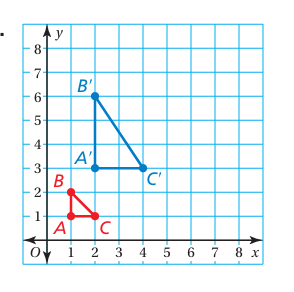
(x,y)->(2x, 3y) ; Each x-coordinate is multiplied by 2 and each y-coordinate is multiplied by 3.

500

The vertices of a triangle are S(2,5), T(3,–1), and U(0,–2). Dilate the triangle using a scale factor of 3. Then translate it 2 units left and 4 units up. What are the coordinates of the image?

S″(4,19), T″(7,1), U″(–2,–2)

500

The ratio of the corresponding side lengths of two similar parallelogram signs is 9 : 14.

What is the ratio of the perimeters? Explain.

What is the ratio of the areas? Explain.

9 : 14; The ratio of the perimeters is equal to the ratio of the corresponding sides.

81 : 196; The ratio of the areas is equal to the square of the ratio of the corresponding sides.