Transformations of Linear Functions
Arithmetic Sequences
Evaluating Functions
Relations and Functions
100
f(x) ---> -f(x) means what transformation is happening?
What is a reflection across the x-axis?
100
A necessary characteristic for a sequence to be classified as an arithmetic sequence
What is a common difference?
100
f(2) if f(x)= 4x-5
What is 3?
100
the coordinates that make up the domain
What are the x-coordinates?
200
The new function if f(x)=4x is translated to the up10 units
What is f(x-10)=4x+10?
200
The name of this formula:
an=a1+(n-1)d
What is explicit?
200
f(6) if f(x)=10-5x
What is -20?
200
The domain of this function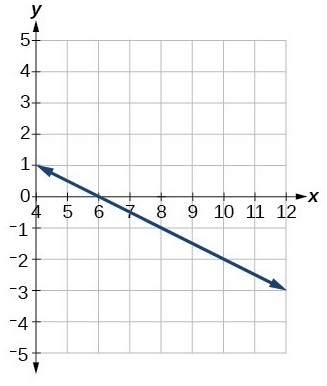
What is
(-oo,oo)
300
The kind of lines produced by translations
What are parallel lines?
300
The situation when you would use a recursive formula instead of an explicit formula
What is when you are looking for the next term?
300
f(4) if
f(x) =1/2 x-5
What is -3?
300
The two stipulations a relation must meet to be considered a one-to-one function
What is every x has one y and every y has one x?
400
The function created by vertically compressing f(x)=10x-6 by a factor of
1/3
What is
1/3f(x)=10/3x-2
400
The simplified explicit formula for this arithmetic sequence:
38, 30, 22, 14, 6, -2, ......
What is an=46-8n?
400
f(1.5) if f(x)=5x-2.35
What is 5.15?
400
The linear function represented by this table: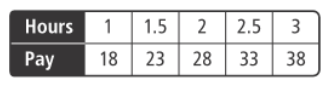
What is f(x)=10x+8?
500
f(x)=4x-2 translated 2 units down and 5 units to the left
What is
f(x+5)-2 =4x+16?
500
The 105th term in the arithmetic sequence represented by an=43+5n
What is 568?
500
The value of x that makes the following true
f(x)=-5/4x-6; f(x)=18
What is
-96/5?
500
The correct range for the following set of points:
{(4,2) , (2,6) , (1,3) , (10,2) , (5,7)}
What is {2,3,6,7}?