Finding Equation with a Slope & a Point
Converting Between Forms of a Linear Equation
Scatter Plots, Correlation & Causation
Finding Inverse Functions
Line Between Two Points
100
Find the equation for a line that goes through point (1,2) with a slope of 3
y = 3x - 1
100
Convert this linear equation into slope-intercept form:
3x + y = 5
y = -3x + 5
100
As you get older, you get taller. Age and height have a [ positive / negative ] correlation
Positive correlation
100
If a function contains the following points, what points will its inverse contain?
(3,5) (6, 4) (-10, -20) (16, -32)
(5,3) (4,6) (-20, -10) (-32, 16)
100
Find the *slope* of the line that passes through (2,3) & (12, 9)
3/5
200
Find the equation for a line that goes through the point (5,3) with a slope of 7
y = 7x - 32
200
Convert this linear equation into standard form:
y = 10x + 7
-10x + y = 7
200
The higher you climb on a mountain, the colder it gets. Altitude and temperature have a [positive / negative] correlation.
Negative correlation
200
Find the inverse function of the following function:
f(x) = x + 8
f-1(x) = x - 8
200
Find the *slope* of the line that passes through (-3, 4) & (6, -7)
-11/9
300
Find the equation for the line between (-2, 6) with a slope of -8
y = -8x - 10
300
Convert this linear equation into standard form:
y = 9x + 14
-9x + y = 14
300
This graph shows [positive / negative / no] correlation
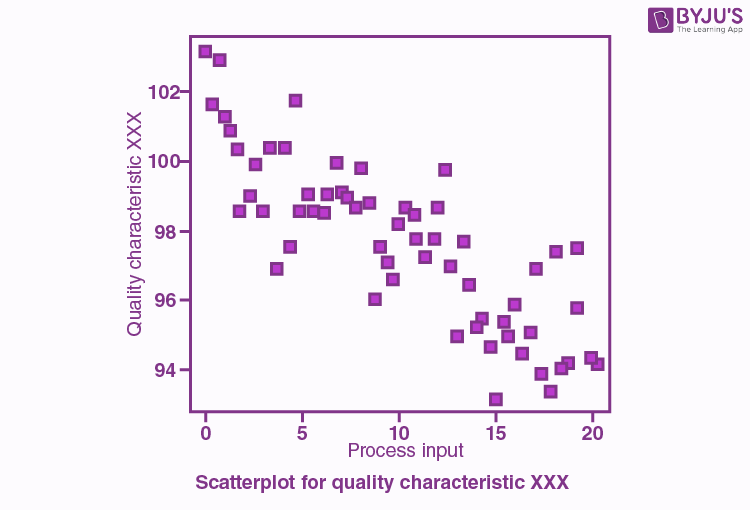
Negative correlation
300
Find the inverse of the following function:
f(x) = 3x - 1
f-1(x) = (x+1)/3
300
Find the slope-intercept *equation* for the line that passes through (3,4) & (4, 6)
y = 2x - 2
400
Find the equation for the line that goes through the point (-11, -22) with a slope of -5.
y = -5x - 77
400
Convert this linear equation into slope-intercept form:
6x + 2y = 12
y = -3x + 6
400
The following scatter plot shows [positive / negative / no] correlation
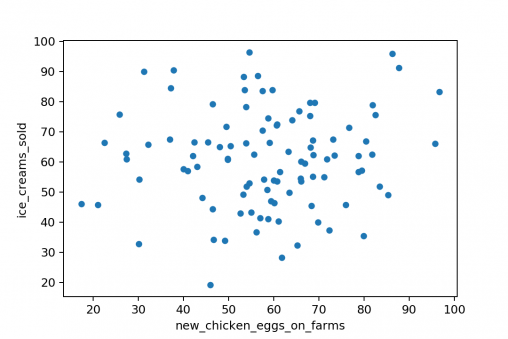
No correlation
400
Find the inverse function for the following function:
f(x) = 4x - 8
f-1(x) = (x+8)/4
400
Find the slope-intercept equation for the line that passes through the points (-2,3) and (2, -5)
y = -2x - 1
500
Is the point (4,3) on the line y = x + 2 ?
No. (4+2 does not equal 3)
500
Convert this linear equation into standard form:
y - 3 = 4(x - 2)
-4x + y = -5
500
A scientist makes a scatter plot for the number of deer in a state park and finds a line of fit with the equation y = 6x + 40 . If x is the number of years after 2020, and y is the number of deer, how many deer will there be in 2030?
100 deer
500
If f(4)=7, then f-1(7)=_____
4
500
Find the slope-intercept equation for the line that passes through the points (-3,-6) and (-7,-12)
y = 1.5x - 1.5