Translations
Reflections
Rotations
Symmetry
Congruence Transformations /
Compositions
Compositions
100
Write the rule for the given transformation:
(x,y) → (x+4, y-2)
<4, -2>
100
Write a rule to describe each transformation:
(In words and in coordinate notation).
Reflection across y=x
(x,y)→(y, x)
100
Write a rule to describe the rotation. Be specific.
(In words and in coordinate notation).
Rotation of 180 °
(x,y)→(-x, -y)
100
Determine how many lines of symmetry the figure has:
5 lines
100
A double reflection of parallel lines is the same as a ________________.
Translation
200
Find the coordinates of the image after the given translation.
W(2,1) → ?
(x,y)→ (x+3, y-6)
W'(5, -5)
200
Write a rule to describe each transformation:
(In words ONLY).
Reflect across x=-2
200
Write a rule to describe the rotation. Be specific.
(In words and in coordinate notation).
Rotation of 90° C C W or
270° C W
(x,y)→(-y, x)
200
Determine how many lines of symmetry there are.
4 lines of symmetry
200
A double reflection over intersecting lines is the same as a _________________.
Rotation
300
Find the coordinates of the vertices of the triangle after the given translation.
W(-1,-5), V(3, -2), U(4, -4)
(x,y)→(x-3, y+3)
W'(-4,-2), V'(0, 1), U'(1, -1)
300
Find the coordinates of the point after the given reflection:
S(-5,-1)
Reflection over the y-axis
S'(5, -1)
300
Rotate the point P(3,-2) around the origin 90° C C W . Give the coordinates of P'.
P'(2,3)
300
The figure has rotational symmetry. Find the order.
Order: 2
300
Describe a congruence transformation that maps △ABC to △A'B'C' .
(Hint: Be careful with the scale!)
Translate 8 units right, 2 units up
(x,y)→(x+8, y+2)
<8, 2>
400
Find the coordinates of the point after translating it along vector <-5, 8> .
D(1, -5)
D'(-4,3)
400
Find the coordinates of the line segment after the given reflection.
Reflect over the x-axis:
C(3,0), D(1, -3)
C'(3,0), D'(1,3)
400
Rotate the point V(-2,-5) around the origin 90° C W . Give the coordinates of V'.
V'(-5,2)
400
The given figure has rotational symmetry. Find the magnitude.
Magnitude/Angle of Rotation: 45 degrees
400
Describe a congruence transformation that maps △ABC to △A'B'C' .
(Hint: 2 actions)
Reflection in the x-axis, followed by a translation 2 units right
500
1st Translation: (x, y) → (x + 2, y − 1),
2nd Translation: (x, y) → (x + 1, y − 2);
Overall Movement: (x, y) → (x + 3, y − 3)
500
After reflecting the figure across the line y=-x , in which quadrant will its image be located?
Quadrant I
500
Point P(4,-1) is rotated 180° about the point C(1,3)
Find the coordinates of the image P'
P'(-2,7)
500
Determine if the figure has linear / rotational symmetry. If so, find how many lines of symmetry, what the order is and what the magnitude is.
4 lines of symmetry
Order: 4
Magnitude: 90 degrees
500
Which figures are congruent? Name a transformation that maps the pre-image onto each image.
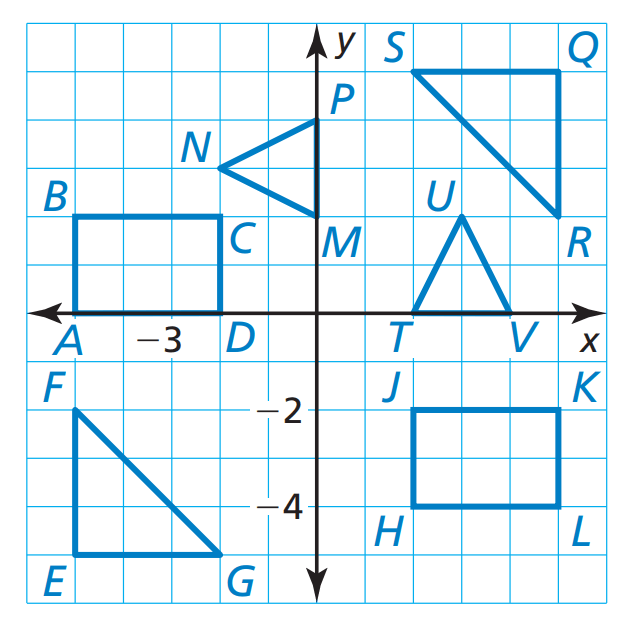
△NPM≅△UVT; Rotate 90 degrees CCW
△FEG≅△RQS; Rotate 180 degrees OR Reflect over y=-x
ABCD≅HJKL; Translate <7,-4>