Isosceles and Equilateral
Congruent Figures
Properties and Theorems
What's Missing?
The unknown
100
When a triangle has 2 congruent sides, it also has congruent what?
Base angles
100
ABCD ≅ XYGH, ∠ G is congruent to which angle?
∠ C
100
A property that states everything is congruent to itself. (think mirror)
Reflexive property
100
What would you need to prove these triangles congruent through ASA?
∠Q≅ ∠F
100
What is the value of x?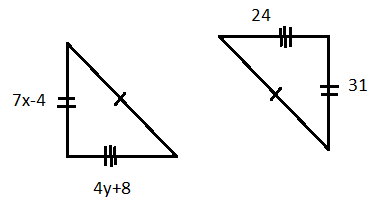
5
200
The measures of an equilateral triangle are...
All equal/all 60 degrees
200
△ADC≅△BCD. ∠ ACD matches up with what angle?
∠BDC
200
A pair of angles opposite each other at an intersection between two lines.
Vertical angles
200
What is needed to prove these triangles are congruent through AAS
∠G≅ ∠P
200
What is the value of y?
4
300
An isosceles triangle has a vertex angle of 70 degrees what are the measures of the base angles?
55 degrees
300
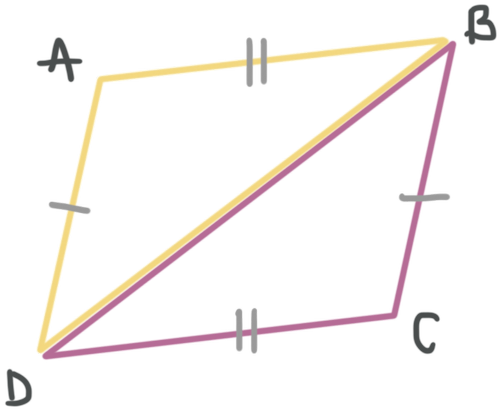
Write a congruence statement for the triangles below.
△ABD≅ △CDB
△BDA ≅△DBC
△DAB≅ △BCD
300
What theorem is used to prove triangles are congruent by using SSA? (Hint we have a right angle)
HL theorem
300
What is missing from these triangles that would allow us to prove them congruent through ASA? 
CE ≅ CD
300
Solve for x so that this is an isosceles triangle
x=2
400
An equilateral triangle has sides of 14 and 7x, what is the measure of x?
2
400
ABCD≅ EFGH x=?
7
400
This theorem states that a triangle with two congruent sides also has 2 congruent base angles.
Isosceles triangle theorem
400
Given AE ≅ CE, What information is needed to prove the triangles congruent by SAS?
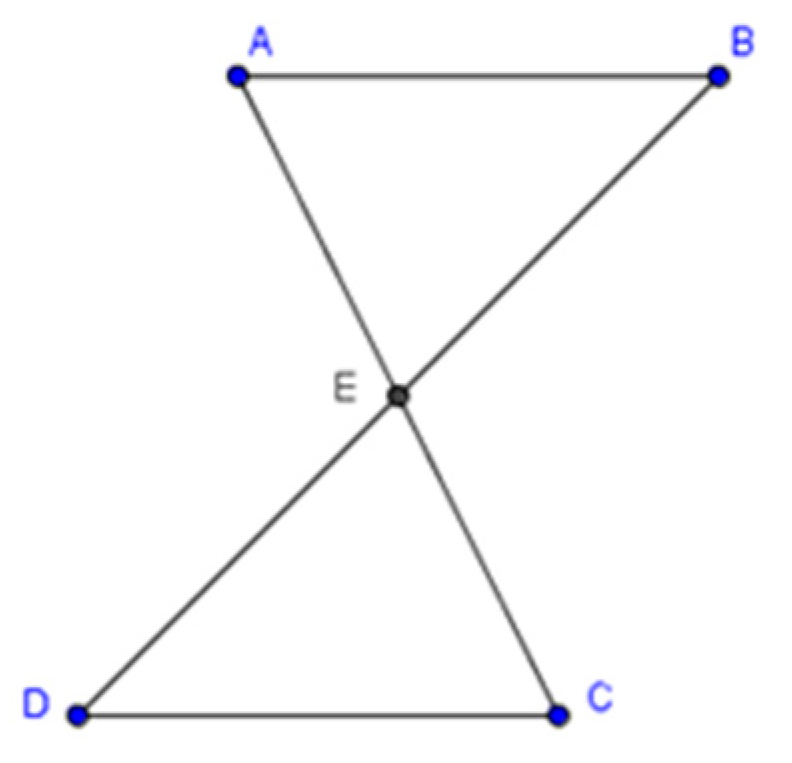
DE ≅EB
400
Solve for x and y.
x=13
y=11
500
What is the value of x?
5
500
ABCD ≅ EFGH y=?
13
500
This theorem states that given two congruent angles in a triangle, the sides opposite those angles must also be congruent.
Converse of the Isosceles triangle theorem
500
Given AC bisects ∠BAD, what else is needed to prove the triangles are congruent through AAS
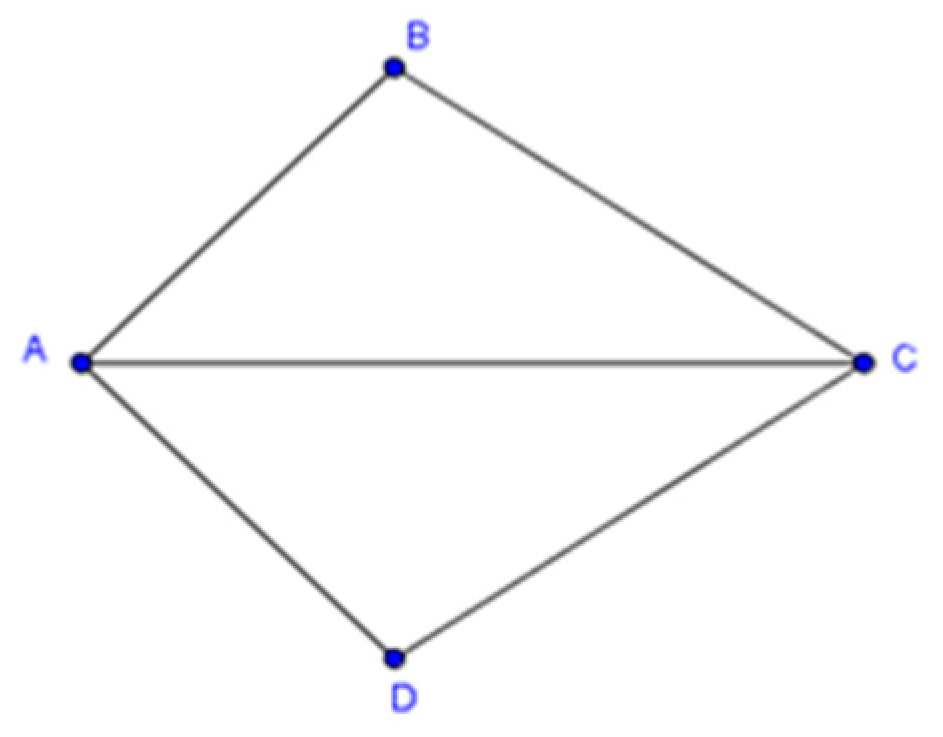
∠B ≅∠D
500
Solve for x and y so the triangles are congruent.
y=2 x=3