Midsegments
Perpendicular/Angle Bisectors, Medians, Altitudes
Centers of Triangles
Inequalities in Triangles
Finding the Centers
100
The midsegment is _____ as long as the side opposite to it.
Half
100
Line AM is called what?
Median
100
The intersection of the perpendicular bisectors is called...
circumcenter
100
Can you create a triangle with the following side lengths?
10.51, 12.5, 23.01
No.
100
Find the circumcenter of a triangle with the following coordinates:
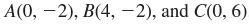
(2,2)
200
The midsegment and the side opposite to it are...
Parallel
200
This line's endpoints are the vertex and the midpoint of the side opposite the vertex.
Median
200
The center of this triangle is called...
Centroid
200
Given the value of two sides, find the range of values for the third side that could make this a triangle.
16.1, 17.2
1.1 < x < 33.3
200
Find the orthocenter of a triangle with the following coordinates:
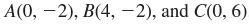
(0,-2)
300
Find x.
x = 13
300
What do we call h?
Altitude
300
Suppose FI = EI = DI. What is the center of this triangle?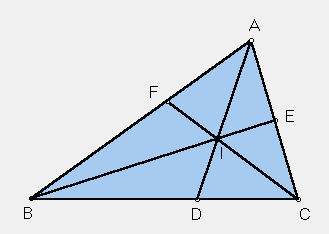
Incenter
300
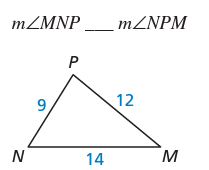
Order the sides from greatest to least:
EF > GF > GE
300
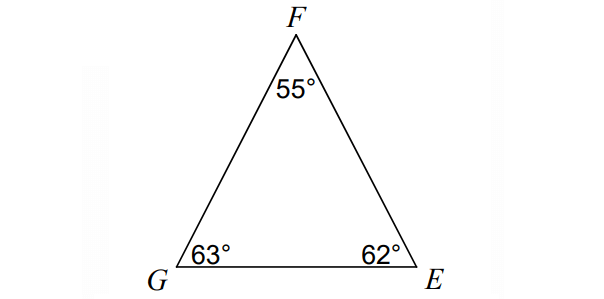
Find the centroid of a triangle with the following coordinates:
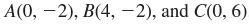
(4/3, 2/3)
400
Find x. 
x = 2
400
What is the length of AD if BC is a perpendicular bisector?
AD = 104
400
Suppose OA = OB = OC. What is the center of this triangle?
Circumcenter
400
In triangle ABC, m<A=56°, m<B=82° and m<C=42° List the sides in order from smallest to largest.
AB, BC, AC
500
Find x and y.
x = 50, y = 70
500
In what kind of triangle would the Perpendicular/Angle Bisectors, Medians, and Altitudes be the same?
An equilateral triangle.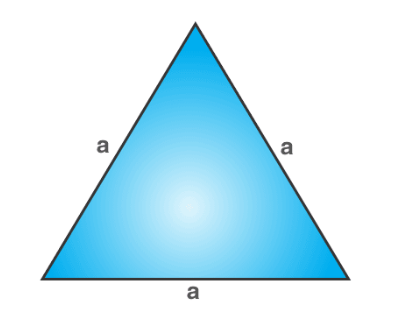
500
Suppose D is the centroid and 12 is the length of DC. Find the length of ED and EC.
ED=6
EC=18
500
<