Chapter 6 Review

Exponents

1

`(4y^-3x^5)/(2y^-2x^3`

`(2x^2)/y`

2

`(2x^3y^5z)^2 (2x^2yz)`

`8x^8y^11z^3`

3

`(2^3x^2y^43z^12)^0`

1

4

`((4x^4y^3z^6)/(2x^2y^4z^2))^2`

`(4x^4z^8)/y^2`

5

`(3x^3y^2z^7)^2(2x^2y^3z^2)^3`

`72x^12y^13z^20`

Scientific Notation

1

Write 29800000 in scientific notation 

2.98 x 10⁷

2

Simplify:

(2.32 x 10³) x (6.25 x 10⁶)

1.46 x 10¹⁰

3

`(6.0*10^-3)/(8.08*10^-2`

7.42 x 10^-2

4

Write 9.78 x 10^-8 in standard form 

.0000000978

5

Simplify: 

(6.3 x 10²)⁶

6.25 x 10¹⁶

Radicals and Rational Exponents

1

Rewrite and evaluate:

`root3 (-125`

-5

2

Rewrite and evaluate:

9^5/2

`(sqrt(9))^5 = 3^5=243`

3

Approximate without your calculator 

`sqrt(60`

7.7

4

Rewrite and evaluate 

(-8)^1/3

`root3(-8) = -2`

5

Rewrite and Evaluate: 

`root3 (-64`

(-64)^1/3 = -4

Exponential Functions (includes growth and decay)

1

Evaluate the given function at the given value:

`h(t)=3*4^t x=-4`

3/64

2

Graph the exponential function f(x) = 2^x

3

Bobby bought a new truck for $50,000, and it decreases in value by 15% every two years. What will the truck cost after 10 years. 

y = 50,000 * .85^t

y = 50,000 * .85⁵

y = $22,185.27

4

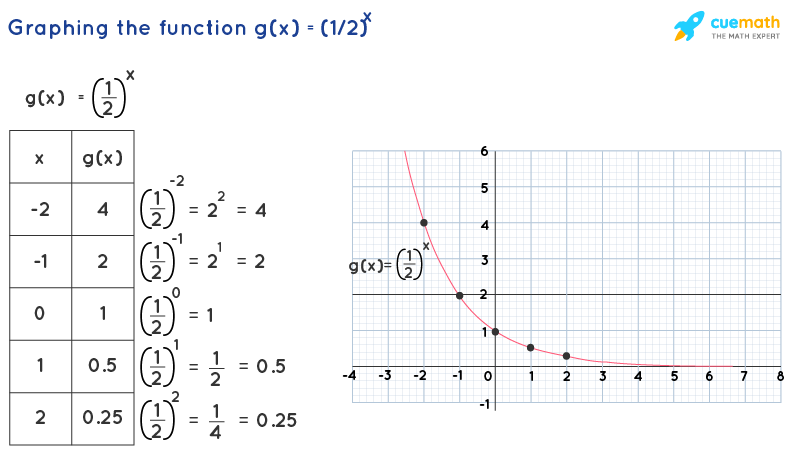
Graph the exponential function g(x) = (1/2)^x

5

A new species of bears have been found. Right now there is 500 of them. They are doubling every quarter of a year. How many bears will there be in 4 years? 

y = 500 * 2^t

y = 500 * 2¹⁶

y = 32,768,000 Bears